

Up: The mass-loss rates of
Subsections
4 Some simple estimates
In this section we describe some simple estimates,
based on general momentum and energy considerations of optically
thick radiation driven winds.
4.1 The opacity at the sonic point
We can obtain a simple estimate of the opacity at the sonic point
of an optically thick wind from the sonic point condition that
the righthand side of the momentum equation should vanish,
so
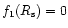 with f1 defined by Eq. (21). The temperature
derivative in an optically thick wind is given by Eq. (16).
These equations predict that
with f1 defined by Eq. (21). The temperature
derivative in an optically thick wind is given by Eq. (16).
These equations predict that
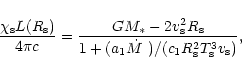 |
(39) |
where we have used the mass continuity equation for the substitution
of  .
The second term of the numerator is much smaller than the
first term, because the sound velocity at the sonic point
(typically about 30 km s-1) is much smaller than the escape velocity
(typically about 2000 km s-1). For reasonable values of
.
The second term of the numerator is much smaller than the
first term, because the sound velocity at the sonic point
(typically about 30 km s-1) is much smaller than the escape velocity
(typically about 2000 km s-1). For reasonable values of  (between 10-5 and 10-4
(between 10-5 and 10-4
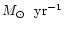 )
and sonic point
temperatures of order 105 K (see below), the second term in the
denominator is much smaller than unity. This is equivalent to the
statement that the two dominant terms in the right hand side of the
momentum equation are the gravity and the radiation pressure, with
the gas pressure terms being negligible. So Eq. (39) reduces to
)
and sonic point
temperatures of order 105 K (see below), the second term in the
denominator is much smaller than unity. This is equivalent to the
statement that the two dominant terms in the right hand side of the
momentum equation are the gravity and the radiation pressure, with
the gas pressure terms being negligible. So Eq. (39) reduces to
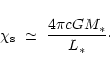 |
(40) |
Using the mass-luminosity relation of H-poor WR-stars, Eq. (53),
we find an estimate of the required opacity for radiation driven
optically thick winds of
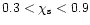 cm2 g-1.
These are reasonable values for hot star winds.
cm2 g-1.
These are reasonable values for hot star winds.
4.2 The opacity gradient at the sonic point
We can derive an important condition for the opacity gradient at the
sonic point of radiation driven winds. From de l'Hopital's rule at
the sonic point (Eq. (26)), combined with the sonic point
condition that f1=0 and f2=0, it is easy to show that the
velocity gradient at the sonic point,
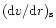 ,
can only be positive
if
,
can only be positive
if
 |
(41) |
The last term is due to the effect of the gradient of the gas
pressure. In a radiation driven wind the force produced by the gas
pressure is by definition negligible compared to the force produced
by the radiation pressure. So we can neglect that term.
Equation (41) thus shows
that in a radiation driven wind with constant L(r)the gradient
 must be positive to allow a transonic
flow. In the case of optically thick radiation driven winds
must be positive to allow a transonic
flow. In the case of optically thick radiation driven winds
 (cf. with Quinn & Paczynski 1985)
and so
(cf. with Quinn & Paczynski 1985)
and so
 must certainly be positive.
must certainly be positive.
We conclude that a stellar wind can only be driven by radiation
pressure if
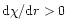 at the sonic point! This implies that
optically thick stellar winds must have their sonic point in the
density and temperature regime where the opacity increases as a
function of distance. This occurs for instance in the region of the
iron opacity peak around
at the sonic point! This implies that
optically thick stellar winds must have their sonic point in the
density and temperature regime where the opacity increases as a
function of distance. This occurs for instance in the region of the
iron opacity peak around
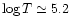 .
.
This condition for the gradient of the opacity of radiation driven
winds is a special case of the general condition that a wind can only
be accelerated through the sonic point if either energy or momentum
is added at the sonic point (cf. Lamers & Cassinelli 1999, p. 100).
4.3 Mass-loss rates of optically thick winds
The energy equation near the sonic point (Eq. (19)) can be
written as
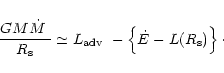 |
(42) |
The test models and the optically thick wind models of the studied
stars (described below in Sect. 5.1 and Table 1)
reveal that
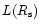 is very close to
is very close to 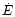 and the absolute
value of
and the absolute
value of
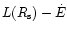 is much smaller than
is much smaller than
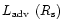 .
This means that we can estimate the mass-loss rate by equating the
advection term with the potential energy term:
.
This means that we can estimate the mass-loss rate by equating the
advection term with the potential energy term:
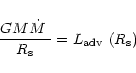 |
(43) |
and after some substitutions we find
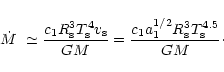 |
(44) |
Approximately the same formula can be derived quite generally
from the following simple considerations.
Let us start with the formulae for
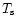 and
and
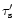 (Eqs. (34) and (35)).
Using Eq. (4) we can express
(Eqs. (34) and (35)).
Using Eq. (4) we can express
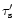 in the form
in the form
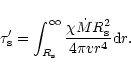 |
(45) |
The ratio 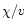 is changing very little in the inner part of the
wind (this is the specific property of optically thick winds of
WR-stars!) and the ratio
is changing very little in the inner part of the
wind (this is the specific property of optically thick winds of
WR-stars!) and the ratio 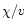 at infinity is only about
two times smaller than at the sonic point.
This property and the steep drop of the integral kernel in
Eq. (45) with increasing r, due to the factor
v-1r-4,
implies that we can estimate
at infinity is only about
two times smaller than at the sonic point.
This property and the steep drop of the integral kernel in
Eq. (45) with increasing r, due to the factor
v-1r-4,
implies that we can estimate
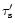 as
as
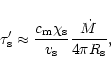 |
(46) |
where 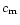 is a multiplier of the order of unity.
The temperature at the sonic point can be expressed approximately as
is a multiplier of the order of unity.
The temperature at the sonic point can be expressed approximately as
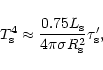 |
(47) |
because
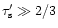 for WR-winds.
Using Eqs. (47) and (46) and
for WR-winds.
Using Eqs. (47) and (46) and
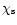 from Eq. (40), we obtain
from Eq. (40), we obtain
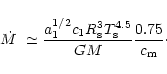 |
(48) |
Note that this formula differs from the Eq. (44)
only by the constant
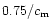 which is very close to unity.
which is very close to unity.
Therefore we can conclude that formula (44) is a very
good approximation formula for deriving the mass-loss rates of WR-stars.
4.4 The minimum mass-loss rate for optically thick winds
We can find the minimum estimated mass-loss rate for the particular
WR-star by using the formula (44) with the
minimim estimate of the temperature at the sonic point derived from
formula Eq. (34) by adopting
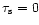 .
This gives a minimum
value of the mass-loss rate of
.
This gives a minimum
value of the mass-loss rate of
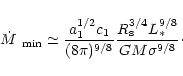 |
(49) |
Applying this equation to a typical hydrogen-free WNE-star with
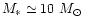 ,
,
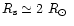 and with the luminosity
given by the M-L law (Eq. (53):
and with the luminosity
given by the M-L law (Eq. (53):
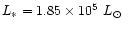 ),
we find a minimum mass-loss rate of about
),
we find a minimum mass-loss rate of about
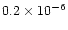
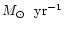 .
.
4.5 The maximum mass-loss rate
An absolute upper limit for the mass-loss rate of radiation driven
winds is set by the condition that all the energy generated in the
nucleus is used to drive the wind. This gives
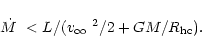 |
(50) |
For a typical hydrogen-free WNE-star with
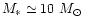 ,
,
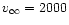 km s-1 and with the
luminosity given by the M-L law
(Eq. (53):
km s-1 and with the
luminosity given by the M-L law
(Eq. (53):
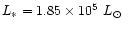 )
and the hydrostatic core radius
given by the evolutionary models (Eq. (54):
)
and the hydrostatic core radius
given by the evolutionary models (Eq. (54):
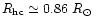 )
we derive
an upper limit of
)
we derive
an upper limit of
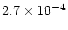
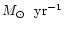 .
.
A more realistic upper limit can be found from the formula Eq. (43)
by using for
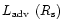 the advective luminosity at
infinity which ought to be higher than
the advective luminosity at
infinity which ought to be higher than
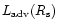 .
In the case of thin winds we know that near the star
.
In the case of thin winds we know that near the star
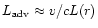 ,
which is much lower than
,
which is much lower than
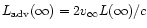 .
In the case of thick winds
we know that
.
In the case of thick winds
we know that
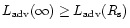 .
So
the upper limit for the mass-loss rate of optically thick winds
can be obtained from the formula
.
So
the upper limit for the mass-loss rate of optically thick winds
can be obtained from the formula
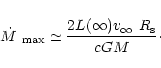 |
(51) |
For a typical WNE-star with the parameters given above
we find that
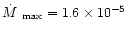
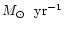 .
The observed mass-loss rates of WNE stars are indeed in between
the minimum and maximum values derived here.
.
The observed mass-loss rates of WNE stars are indeed in between
the minimum and maximum values derived here.


Up: The mass-loss rates of
Copyright ESO 2002
![]() with f1 defined by Eq. (21). The temperature
derivative in an optically thick wind is given by Eq. (16).
These equations predict that
with f1 defined by Eq. (21). The temperature
derivative in an optically thick wind is given by Eq. (16).
These equations predict that
![]() ,
can only be positive
if
,
can only be positive
if
![]() at the sonic point! This implies that
optically thick stellar winds must have their sonic point in the
density and temperature regime where the opacity increases as a
function of distance. This occurs for instance in the region of the
iron opacity peak around
at the sonic point! This implies that
optically thick stellar winds must have their sonic point in the
density and temperature regime where the opacity increases as a
function of distance. This occurs for instance in the region of the
iron opacity peak around
![]() .
.
![]() .
This gives a minimum
value of the mass-loss rate of
.
This gives a minimum
value of the mass-loss rate of
![]() the advective luminosity at
infinity which ought to be higher than
the advective luminosity at
infinity which ought to be higher than
![]() .
In the case of thin winds we know that near the star
.
In the case of thin winds we know that near the star
![]() ,
which is much lower than
,
which is much lower than
![]() .
In the case of thick winds
we know that
.
In the case of thick winds
we know that
![]() .
So
the upper limit for the mass-loss rate of optically thick winds
can be obtained from the formula
.
So
the upper limit for the mass-loss rate of optically thick winds
can be obtained from the formula