

Up: The mass-loss rates of
Subsections
In this section we will derive the equations that describe the
flow of the radiation and gas in the optically thick part of the
wind. The wind has to be accelerated from subsonic velocities
deep down in the atmosphere to supersonic velocities in the wind.
This implies that the wind must pass smoothly through the sonic point
where the flowspeed is equal to the local sound speed. We first
describe the general equations for radiation driven winds.
We then apply these to the sonic point. The requirement of a smooth
transonic flow sets specific conditions to the values and gradients
of several parameters, including the mass-loss rate. We will derive
these conditions.
2.1 General equations for radiation driven winds
We assume that the winds of WR-stars can be described by a steady,
spherically-symmetric flow. The fluid flow equations for radiatively
driven winds are:
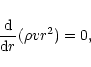 |
(1) |
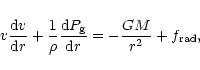 |
(2) |
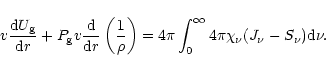 |
(3) |
These equations express conservation of respectively mass, momentum
and energy of the gas. The symbols are the mass density 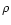 ,
the
gas pressure
,
the
gas pressure 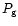 ,
the velocity v, the (angle-) mean intensity
of radiation
,
the velocity v, the (angle-) mean intensity
of radiation 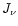 ,
the mass extinction (absortion + scattering)
coefficient
,
the mass extinction (absortion + scattering)
coefficient
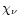 ,
the radiative source function
,
the radiative source function 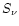 ,
the internal energy
,
the internal energy 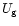 of the gas per unit mass, the stellar
mass M and the force
of the gas per unit mass, the stellar
mass M and the force
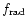 produced by radiation pressure.
The mass-loss rate of the star is
produced by radiation pressure.
The mass-loss rate of the star is
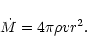 |
(4) |
The gas pressure 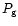 depends on temperature T and density
depends on temperature T and density 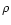 as
as
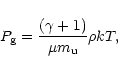 |
(5) |
where 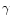 is the mean number of free electrons per atom,
is the mean number of free electrons per atom,
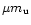 is
the mean atomic weight and
is
the mean atomic weight and 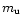 is the atomic mass unit. The internal
energy
is the atomic mass unit. The internal
energy 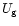 is related to
is related to 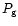 by the rule
by the rule
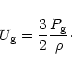 |
(6) |
The isothermal sound speed is given by
 |
(7) |
Using the formulae (1), (5) and (7) we can
transform the momentum Eq. (2) into the form
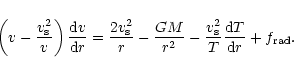 |
(8) |
The radiation pressure force is
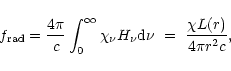 |
(9) |
where 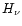 is the first moment of the radiation intensity
(the Eddington flux), L(r) is the radiative luminosity
in the frame comoving with the wind and
is the first moment of the radiation intensity
(the Eddington flux), L(r) is the radiative luminosity
in the frame comoving with the wind and 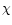 is the flux-mean
opacity (the flux-mean extinction (absorption + scattering)
coefficient per unit mass).
is the flux-mean
opacity (the flux-mean extinction (absorption + scattering)
coefficient per unit mass).
The integrated overall energy conservation equation for both
the gas and the radiation is
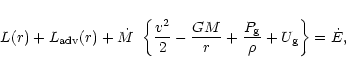 |
(10) |
where 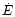 is the energy-loss constant (the total energy transported
out per unit time across any spherical surface). The first term is
the luminosity L(r) in the comoving frame.
The second term is the radiative energy that is carried out (advected)
by the gas flow in the comoving frame.
Cassinelli & Castor (1973) have shown that the advective
luminosity
is the energy-loss constant (the total energy transported
out per unit time across any spherical surface). The first term is
the luminosity L(r) in the comoving frame.
The second term is the radiative energy that is carried out (advected)
by the gas flow in the comoving frame.
Cassinelli & Castor (1973) have shown that the advective
luminosity
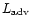 is
is
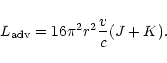 |
(11) |
This term is independent of 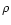 because the radiation density is
independent of
because the radiation density is
independent of 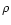 .
At large distance from the star the moments of
the radiation approach
.
At large distance from the star the moments of
the radiation approach
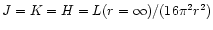 and so
and so
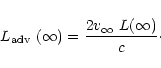 |
(12) |
The sum of L(r) and
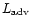 is the luminosity in the stationary
frame (see Cassinelli & Castor 1973; Pistinner & Eichler
1995).
The third term in Eq. (10) is the total gas energy (kinetic,
thermal and potential) that is advected by the flow.
is the luminosity in the stationary
frame (see Cassinelli & Castor 1973; Pistinner & Eichler
1995).
The third term in Eq. (10) is the total gas energy (kinetic,
thermal and potential) that is advected by the flow.
The energy-loss constant 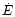 can be found from general
considerations.
The energy rate
can be found from general
considerations.
The energy rate
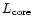 generated by the nuclear
fusion must be equal to the luminosity at infinity plus the
energy lost by accelerating the wind and lifting it out of the
potential well (cf. Heger & Langer 1996):
generated by the nuclear
fusion must be equal to the luminosity at infinity plus the
energy lost by accelerating the wind and lifting it out of the
potential well (cf. Heger & Langer 1996):
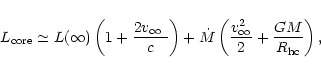 |
(13) |
where
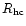 is the radius of the hydrostatic core.
We see from Eqs. (10) and (12) that
is the radius of the hydrostatic core.
We see from Eqs. (10) and (12) that
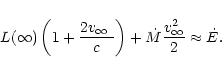 |
(14) |
From these two equations we obtain an expression for the
energy loss constant
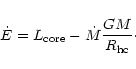 |
(15) |
2.2 The optically thick part of the wind
The momentum Eq. (8) and the energy Eq. (10) together describe the radiation driven wind.
The solution of these equations requires knowledge about the
opacity and the temperature structure. For the optically thick
part of the wind we can make some simplifying approximations,
because the transfer of radiation can be described by diffusion.
In the case of radiative diffusion the temperature gradient is
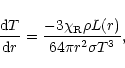 |
(16) |
and the radiation-pressure force is
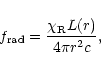 |
(17) |
where
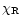 is the Rosseland mean opacity. In the optically
thick part of the wind the mean intensity
of the radiation is
is the Rosseland mean opacity. In the optically
thick part of the wind the mean intensity
of the radiation is
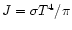 and K=J/3
(Cassinelli & Castor 1973) and so the advective luminosity
(Eq. (11)) is
and K=J/3
(Cassinelli & Castor 1973) and so the advective luminosity
(Eq. (11)) is
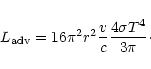 |
(18) |
Defining the constants
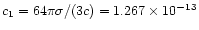 and
and
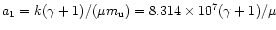 in cgs-units, where
in cgs-units, where 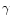 is the mean number of free
electrons per ion,
we can write the energy equation in the optically
thick part of the
wind as
is the mean number of free
electrons per ion,
we can write the energy equation in the optically
thick part of the
wind as
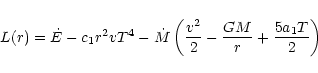 |
(19) |
This is the form of the energy equation that we will use to find
the radiative luminosity L(r) in the comoving frame that
is needed for the calculation of the radiative force
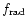 .
.
The diffusion approximation becomes valid at large
optical depths (i.e., many photon mean-free-paths below the surface) where
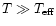 (Mihalas 1978, p. 49).
For an estimate, let us adopt that if the photon mean-free-path is
more than 10 times smaller than the sonic point radius then the diffusion
approximation is valid.
The photon mean-free-path (
(Mihalas 1978, p. 49).
For an estimate, let us adopt that if the photon mean-free-path is
more than 10 times smaller than the sonic point radius then the diffusion
approximation is valid.
The photon mean-free-path (
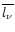 )
is defined as
)
is defined as
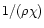 .
Using the sonic point parameters from the paper (see
Table 7), we
find that in the case of the WN6 star WR136
.
Using the sonic point parameters from the paper (see
Table 7), we
find that in the case of the WN6 star WR136
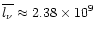 cm
(
cm
(
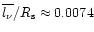 )
and in the case of the WN5
star WR 139
)
and in the case of the WN5
star WR 139
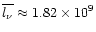 cm (
cm (
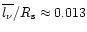 ). Thus, the diffusion
approximation is valid for the regions near the sonic
points of WR-star winds. Note that this is not the case for the winds of
O-stars, which generally have
). Thus, the diffusion
approximation is valid for the regions near the sonic
points of WR-star winds. Note that this is not the case for the winds of
O-stars, which generally have
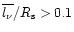 .
.
2.3 The conditions at the sonic point
The momentum Eq. (8) has the characteristic form of
an equation with a critical point. The left hand side shows
that when
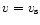 ,
the velocity gradient
,
the velocity gradient
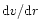 becomes infinite
(positive or negative), unless the right hand side is zero at this
sonic point. So the right hand side must vanish exactly at the
critical point.
The smooth passage of the flow through the sonic point also requires
that the derivatives of the temperature and velocity are equal on both
sides of the sonic point. These conditions are expressed by the
de l'Hopital rule which describes the relations for the
radial velocity gradients at the critical point
(see e.g. Lamers & Cassinelli 1999, p. 421).
becomes infinite
(positive or negative), unless the right hand side is zero at this
sonic point. So the right hand side must vanish exactly at the
critical point.
The smooth passage of the flow through the sonic point also requires
that the derivatives of the temperature and velocity are equal on both
sides of the sonic point. These conditions are expressed by the
de l'Hopital rule which describes the relations for the
radial velocity gradients at the critical point
(see e.g. Lamers & Cassinelli 1999, p. 421).
The momentum Eq. (8) can be written as
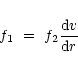 |
(20) |
with
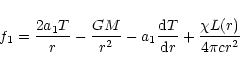 |
(21) |
and
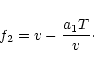 |
(22) |
The conditions at the sonic point, 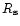 ,
where the flow
velocity is
,
where the flow
velocity is
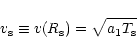 |
(23) |
with
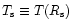 are
are
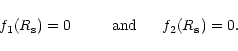 |
(24) |
The first condition implies that
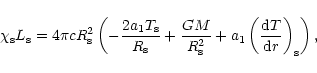 |
(25) |
where the subscript  denotes the values at the sonic point.
The velocity gradient at the sonic point is given by de l'Hopital's
rule
denotes the values at the sonic point.
The velocity gradient at the sonic point is given by de l'Hopital's
rule
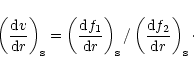 |
(26) |
Since f2 increases from negative below the sonic point to positive
above the sonic point, the gradient
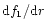 should be positive
at the sonic point. In physical terms this means that either energy
or momentum must be added to the wind as it passes through the
sonic point (cf. Lamers & Cassinelli 1999, p. 100).
The requirement that the velocity gradient should be continuous
through the sonic point (i.e. the regularity condition) implies that
should be positive
at the sonic point. In physical terms this means that either energy
or momentum must be added to the wind as it passes through the
sonic point (cf. Lamers & Cassinelli 1999, p. 100).
The requirement that the velocity gradient should be continuous
through the sonic point (i.e. the regularity condition) implies that
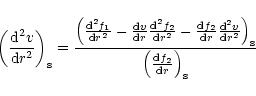 |
(27) |
with the derivatives
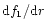 ,
,
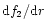 ,
,
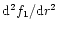 and
and
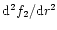 following
from the definitions of f1 and f2.
following
from the definitions of f1 and f2.
We point out that the CAK-type line forces (actually the line force
amplification due to Doppler shifts - Castor et al. 1975) can
be neglected near the sonic point of WR-star winds.
The CAK-type line force is usually expressed in relation to the
radiation force by electron scattering as follows
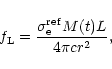 |
(28) |
where
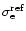 is the reference value for the electron
scattering opacity (
is the reference value for the electron
scattering opacity (
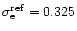 cm2g-1, Lamers & Cassinelli 1999,
p. 217).
The force multiplier can be expressed as
cm2g-1, Lamers & Cassinelli 1999,
p. 217).
The force multiplier can be expressed as
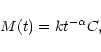 |
(29) |
where k and 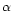 are the force multiplier parameters, C is a
correction term which is very close to unity and t is the
dimensionless optical depth parameter defined as
are the force multiplier parameters, C is a
correction term which is very close to unity and t is the
dimensionless optical depth parameter defined as
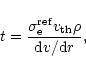 |
(30) |
where
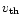 is the mean thermal velocity of protons.
Our optically thick wind models show that
is the mean thermal velocity of protons.
Our optically thick wind models show that
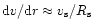 near the sonic point.
The value of t at the sonic point can be found
from the relationship
near the sonic point.
The value of t at the sonic point can be found
from the relationship
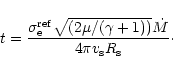 |
(31) |
This shows that near the sonic point of the WN6 star
WR136
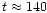 (
(
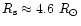 )
and
near the sonic point of
WN5 star WR139
)
and
near the sonic point of
WN5 star WR139
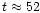 (
(
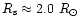 ).
With such large values of t and with the expected
values of
).
With such large values of t and with the expected
values of 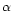 (
(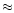 0.5) and k (
0.5) and k (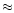 0.6-0.7),
the force multiplier is indeed very small, M(t)<0.05 to 0.08.
This implies that the
CAK-type line force due to Doppler shifts is negligible compared
to electron scattering and other radiation forces near the sonic
points of WR-stars.
One might counterargue that the velocity gradient near the sonic
point might be of order
0.6-0.7),
the force multiplier is indeed very small, M(t)<0.05 to 0.08.
This implies that the
CAK-type line force due to Doppler shifts is negligible compared
to electron scattering and other radiation forces near the sonic
points of WR-stars.
One might counterargue that the velocity gradient near the sonic
point might be of order
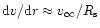 ,
as in optically thin (in the continuum) CAK-type O-star wind models,
rather than
,
as in optically thin (in the continuum) CAK-type O-star wind models,
rather than
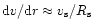 .
If that were the case, the values of t
near the sonic points of WR-stars would be smaller than given above
(
.
If that were the case, the values of t
near the sonic points of WR-stars would be smaller than given above
(
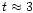 for WR136 and
for WR136 and
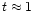 for WR139), but the force
multiplier is still very small
0.3 < M(t) <0.6 compared to
for WR139), but the force
multiplier is still very small
0.3 < M(t) <0.6 compared to
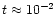 and
M(t)>101 for O-stars.
In this estimate we neglected
continuum absorption within the Sobolev length. This implies that the
true CAK-forces near the sonic points of WR-star winds are even
smaller than estimated above.
So, we can safely conclude that near the sonic points of WR-star winds the
CAK-type forces are not important,
but they become the dominate driving force starting from some distance above
the sonic point. The influence of these forces is not ignored in our models -
they
are taken into account indirectly by using the momentum equation in the
supersonic part of the wind by
assuming that the winds are radiatively driven.
and
M(t)>101 for O-stars.
In this estimate we neglected
continuum absorption within the Sobolev length. This implies that the
true CAK-forces near the sonic points of WR-star winds are even
smaller than estimated above.
So, we can safely conclude that near the sonic points of WR-star winds the
CAK-type forces are not important,
but they become the dominate driving force starting from some distance above
the sonic point. The influence of these forces is not ignored in our models -
they
are taken into account indirectly by using the momentum equation in the
supersonic part of the wind by
assuming that the winds are radiatively driven.
2.4 The temperature structure
The conditions at the sonic point, described above, contain
the derivatives of the temperature T(r), which depends on
the velocity v(r) structure. In this section we describe these
two functions.
From the analytical solution of the spherically extended
atmosphere in radiative equilibrium in the generalized Eddington
approximation derived by Lucy (1971) we find that
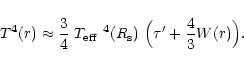 |
(32) |
In this expression
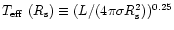 where
where 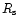 is the radius of the sonic point of
the wind,
W(r) is the coefficient of geometrical dilution, and the effective
optical depth
is the radius of the sonic point of
the wind,
W(r) is the coefficient of geometrical dilution, and the effective
optical depth
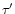 is defined by
is defined by
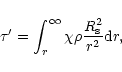 |
(33) |
where 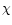 is the flux-mean extinction coefficient.
We point out that Heger & Langer (1996) and
Lucy & Abbott (1993) used a slightly different version of
the original Lucy (1971) formula. They used the photospheric
radius (
is the flux-mean extinction coefficient.
We point out that Heger & Langer (1996) and
Lucy & Abbott (1993) used a slightly different version of
the original Lucy (1971) formula. They used the photospheric
radius (
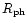 where
where
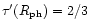 )
as a reference
level,
whereas below the photospheric radius the geometrical dilution was neglected.
Test computations have shown that our results (described below) would
have been qualitatively the same if we had adopted this same
reference level
)
as a reference
level,
whereas below the photospheric radius the geometrical dilution was neglected.
Test computations have shown that our results (described below) would
have been qualitatively the same if we had adopted this same
reference level
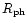 instead of the value of
instead of the value of 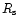 that we
adopted.
The important argument against the use of
that we
adopted.
The important argument against the use of
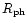 as reference level
is the large difference between
as reference level
is the large difference between
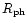 and
and 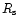 for WR-stars.
Therefore the effects of geometrical dilution should not be neglected in the
region below
for WR-stars.
Therefore the effects of geometrical dilution should not be neglected in the
region below
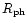 ,
where J/K is not constant.
Our approach is almost in line
with the arguments of the optically thick wind modeling study of
the
,
where J/K is not constant.
Our approach is almost in line
with the arguments of the optically thick wind modeling study of
the
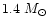 stars driven by super-Eddington luminosities by
Quinn & Paczynski (1985). They stated (p. 635 in their paper) that
"Models of radiatively driven winds with a critical point at a large
optical depth have very diffuse photospheres with the density
scale height approximately equal to the local radius. Therefore,
the variation of radiation energy density with radius is due not only
to diffusion through opaque matter, but also to geometrical dilution''.
stars driven by super-Eddington luminosities by
Quinn & Paczynski (1985). They stated (p. 635 in their paper) that
"Models of radiatively driven winds with a critical point at a large
optical depth have very diffuse photospheres with the density
scale height approximately equal to the local radius. Therefore,
the variation of radiation energy density with radius is due not only
to diffusion through opaque matter, but also to geometrical dilution''.
We adopt the temperature structure of a spherically symmetric
stationary wind in radiative equilibrium, given by Eq. (32)
with the effective optical depth given by Eq. (33).
This approximation is not valid
at distances larger than
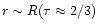 ,
because
it assumes that
,
because
it assumes that
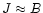 .
For example Eq. (32)
predicts that at large distance from the star, where
.
For example Eq. (32)
predicts that at large distance from the star, where
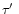 becomes
very small, the temperature will go to zero. In reality the
observations and empirical wind models show that the temperatures of
WR-winds approach a constant finite value of order 104 K at
distances of a few tens of stellar radii. This is due to the radiative
heating by photoionization. Nugis et al. (1998) have determined the
asymptotic temperatures
becomes
very small, the temperature will go to zero. In reality the
observations and empirical wind models show that the temperatures of
WR-winds approach a constant finite value of order 104 K at
distances of a few tens of stellar radii. This is due to the radiative
heating by photoionization. Nugis et al. (1998) have determined the
asymptotic temperatures
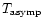 of WR-winds as a function of
WR-subtypes. We adopt these values. So the temperature structure
of our models is described by Eq. (32)
if
of WR-winds as a function of
WR-subtypes. We adopt these values. So the temperature structure
of our models is described by Eq. (32)
if
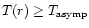 and
and
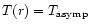 where
Eq. (32) would predict a smaller value. We should point
out that the choice of
where
Eq. (32) would predict a smaller value. We should point
out that the choice of
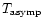 plays only a minor role in our
modeling, as most of the important physical effects occur in the
optically thick part of the wind.
plays only a minor role in our
modeling, as most of the important physical effects occur in the
optically thick part of the wind.
The temperature at the sonic point is
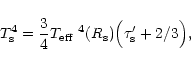 |
(34) |
with an effective optical depth
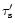 at the sonic point
at the sonic point
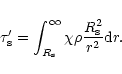 |
(35) |
Notice that 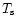 depends on the effective optical depth at the sonic
point and hence on the run of
depends on the effective optical depth at the sonic
point and hence on the run of 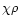 at all layers above
at all layers above
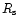 .
Therefore we can only find the solution of the momentum and
energy equations at the sonic point if we know the functions
.
Therefore we can only find the solution of the momentum and
energy equations at the sonic point if we know the functions 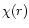 and
and 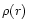 at
at
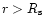 .
.
For determining the distribution of the flux-mean opacity in the wind,
we use the approach of Lucy & Abbott (1993) who derived 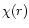 from the demand of the momentum conservation in the wind for an
adopted velocity law. This requirement follows from Eqs.
(8) and (16):
from the demand of the momentum conservation in the wind for an
adopted velocity law. This requirement follows from Eqs.
(8) and (16):
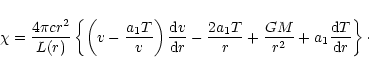 |
(36) |
So for a given v(r), T(r) and L(r) the function 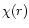 is
known. Note that
is
known. Note that 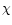 and v are related so that
and v are related so that 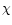 increases with the increase of v. The term consisting of
increases with the increase of v. The term consisting of
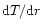 is
very small and is found by using the diffusion approximation for
is
very small and is found by using the diffusion approximation for
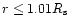 and by differentiating the temperature formula
for
and by differentiating the temperature formula
for
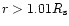 .
.
The value of L(r) is very close to
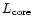 throughout the optically
thick and optically thin part of the wind. This is because the
other terms in the energy Eq. (19), i.e.
throughout the optically
thick and optically thin part of the wind. This is because the
other terms in the energy Eq. (19), i.e.
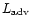 and the
flow of potential, kinetic energy and enthalpy, are all very small
compared to
and the
flow of potential, kinetic energy and enthalpy, are all very small
compared to
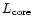 for WR-stars. So in principle we could have
used
for WR-stars. So in principle we could have
used
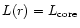 for the calculation of
for the calculation of 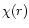 with Eq. (36).
In the computations we took the other terms into
account properly for the calculation of L(r). For the value of
with Eq. (36).
In the computations we took the other terms into
account properly for the calculation of L(r). For the value of
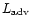 in the calculation of L(r) we used the following scheme:
for the optically thick part we calculated
in the calculation of L(r) we used the following scheme:
for the optically thick part we calculated
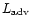 from Eq. (18)
and for the optically thin part we used
from Eq. (18)
and for the optically thin part we used
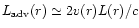 ,
which is valid if
,
which is valid if
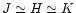 (see Eq. (12)).
In any case, the exact value of
(see Eq. (12)).
In any case, the exact value of
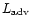 makes a difference of less
than 1 percent in the calculation of
makes a difference of less
than 1 percent in the calculation of 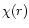 .
.
2.5 The velocity structure
The density in the supersonic part of the wind, which is needed for
the calculation of 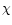 and T(r), can be expressed in terms of
the mass-loss rate and the velocity law. The velocity law in the
supersonic part of the wind is approximately a
and T(r), can be expressed in terms of
the mass-loss rate and the velocity law. The velocity law in the
supersonic part of the wind is approximately a 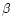 -law:
-law:
 |
(37) |
with the value of
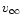 taken from the observations and the value
of
taken from the observations and the value
of 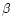 still to be determined. However, near the sonic point the
velocity must deviate from this
still to be determined. However, near the sonic point the
velocity must deviate from this 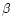 -law, because it would imply
that
-law, because it would imply
that
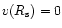 ,
which contradicts the definition of the sonic point.
Therefore we adopt a velocity law in the region of
,
which contradicts the definition of the sonic point.
Therefore we adopt a velocity law in the region of
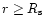 of the
type
of the
type
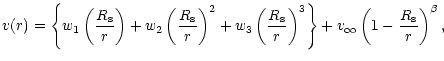 |
|
|
(38) |
with
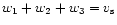 .
The
.
The  -law is only valid for
-law is only valid for
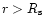 .
This expression for v(r) is practical for our purpose because
(i) the first three terms are small and quickly vanish for
.
This expression for v(r) is practical for our purpose because
(i) the first three terms are small and quickly vanish for
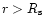 and (ii) the critial point conditions of Eqs. (26) and (27) directly describe the values of w1 and w2 with w3 adjustable to give
and (ii) the critial point conditions of Eqs. (26) and (27) directly describe the values of w1 and w2 with w3 adjustable to give
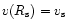 .
.
We stress that the second part of the expression for v(r),
i.e. the 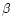 -law, only enters into our analysis for the
calculation of the velocity and density structure in the supersonic
part of the wind. For the analysis of the sonic point conditions
only the first part is important. This is equivalent to the statement
that the
-law, only enters into our analysis for the
calculation of the velocity and density structure in the supersonic
part of the wind. For the analysis of the sonic point conditions
only the first part is important. This is equivalent to the statement
that the 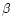 -law does not start exactly at
-law does not start exactly at 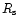 but at some
slightly larger distance where the power-law part slowly merges with
the
but at some
slightly larger distance where the power-law part slowly merges with
the 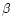 -law. (In principle we could have chosen a more elaborate
expression for the velocity law that ensures a smooth transition from
the subsonic to the supersonic part, than the one adopted here,
but that would not have improved the analysis of the sonic point conditions.)
-law. (In principle we could have chosen a more elaborate
expression for the velocity law that ensures a smooth transition from
the subsonic to the supersonic part, than the one adopted here,
but that would not have improved the analysis of the sonic point conditions.)
2.6 The opacity gradient near the sonic point
If the velocity law and the temperature structure are known, as
described above, then the product
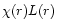 can be found from
Eq. (36). The solution of the critical point equations, which
will give the mass-loss
rate, requires knowledge of the gradients of the optical
depth and of the radiative luminosity near the sonic point.
In normal modeling of a stellar wind one would assume that
can be found from
Eq. (36). The solution of the critical point equations, which
will give the mass-loss
rate, requires knowledge of the gradients of the optical
depth and of the radiative luminosity near the sonic point.
In normal modeling of a stellar wind one would assume that
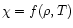 is known and then solve the structure of the wind
and find the mass-loss rate. However, as argued in the introduction,
the flux-mean opacity in the atmospheres of WR-stars is not known.
Therefore, the purpose of our paper is just the opposite:
we try to find what the conditions for
is known and then solve the structure of the wind
and find the mass-loss rate. However, as argued in the introduction,
the flux-mean opacity in the atmospheres of WR-stars is not known.
Therefore, the purpose of our paper is just the opposite:
we try to find what the conditions for 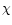 are that could explain
the observed mass-loss rates in terms of optically thick radiation
driven winds. A consequence of this approach is that we do not
know
are that could explain
the observed mass-loss rates in terms of optically thick radiation
driven winds. A consequence of this approach is that we do not
know 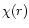 ,
nor its gradient near the sonic point. Instead,
we derive it from the requirement that the model must produce the
observed mass-loss rate.
,
nor its gradient near the sonic point. Instead,
we derive it from the requirement that the model must produce the
observed mass-loss rate.
If the gradient of L(r) is known we can derive the gradient of
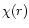 from the derivative of Eq. (36) and vice versa.
Therefore we adopt two methods to estimate these gradients:
variants A and B. In the first one we make an assumption about
L(r) and find the gradient of
from the derivative of Eq. (36) and vice versa.
Therefore we adopt two methods to estimate these gradients:
variants A and B. In the first one we make an assumption about
L(r) and find the gradient of 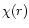 .
In variant B
we make an assumption about the variation of
.
In variant B
we make an assumption about the variation of 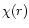 and find the
gradient of L(r). In our modeling we will use both variants
and show that the results are quite similar. We describe these
two variants in more detail in the next section.
and find the
gradient of L(r). In our modeling we will use both variants
and show that the results are quite similar. We describe these
two variants in more detail in the next section.


Up: The mass-loss rates of
Copyright ESO 2002
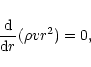
![]() can be found from general
considerations.
The energy rate
can be found from general
considerations.
The energy rate
![]() generated by the nuclear
fusion must be equal to the luminosity at infinity plus the
energy lost by accelerating the wind and lifting it out of the
potential well (cf. Heger & Langer 1996):
generated by the nuclear
fusion must be equal to the luminosity at infinity plus the
energy lost by accelerating the wind and lifting it out of the
potential well (cf. Heger & Langer 1996):
![]() (Mihalas 1978, p. 49).
For an estimate, let us adopt that if the photon mean-free-path is
more than 10 times smaller than the sonic point radius then the diffusion
approximation is valid.
The photon mean-free-path (
(Mihalas 1978, p. 49).
For an estimate, let us adopt that if the photon mean-free-path is
more than 10 times smaller than the sonic point radius then the diffusion
approximation is valid.
The photon mean-free-path (
![]() )
is defined as
)
is defined as
![]() .
Using the sonic point parameters from the paper (see
Table 7), we
find that in the case of the WN6 star WR136
.
Using the sonic point parameters from the paper (see
Table 7), we
find that in the case of the WN6 star WR136
![]() cm
(
cm
(
![]() )
and in the case of the WN5
star WR 139
)
and in the case of the WN5
star WR 139
![]() cm (
cm (
![]() ). Thus, the diffusion
approximation is valid for the regions near the sonic
points of WR-star winds. Note that this is not the case for the winds of
O-stars, which generally have
). Thus, the diffusion
approximation is valid for the regions near the sonic
points of WR-star winds. Note that this is not the case for the winds of
O-stars, which generally have
![]() .
.
![]() ,
the velocity gradient
,
the velocity gradient
![]() becomes infinite
(positive or negative), unless the right hand side is zero at this
sonic point. So the right hand side must vanish exactly at the
critical point.
The smooth passage of the flow through the sonic point also requires
that the derivatives of the temperature and velocity are equal on both
sides of the sonic point. These conditions are expressed by the
de l'Hopital rule which describes the relations for the
radial velocity gradients at the critical point
(see e.g. Lamers & Cassinelli 1999, p. 421).
becomes infinite
(positive or negative), unless the right hand side is zero at this
sonic point. So the right hand side must vanish exactly at the
critical point.
The smooth passage of the flow through the sonic point also requires
that the derivatives of the temperature and velocity are equal on both
sides of the sonic point. These conditions are expressed by the
de l'Hopital rule which describes the relations for the
radial velocity gradients at the critical point
(see e.g. Lamers & Cassinelli 1999, p. 421).
![]() ,
because
it assumes that
,
because
it assumes that
![]() .
For example Eq. (32)
predicts that at large distance from the star, where
.
For example Eq. (32)
predicts that at large distance from the star, where
![]() becomes
very small, the temperature will go to zero. In reality the
observations and empirical wind models show that the temperatures of
WR-winds approach a constant finite value of order 104 K at
distances of a few tens of stellar radii. This is due to the radiative
heating by photoionization. Nugis et al. (1998) have determined the
asymptotic temperatures
becomes
very small, the temperature will go to zero. In reality the
observations and empirical wind models show that the temperatures of
WR-winds approach a constant finite value of order 104 K at
distances of a few tens of stellar radii. This is due to the radiative
heating by photoionization. Nugis et al. (1998) have determined the
asymptotic temperatures
![]() of WR-winds as a function of
WR-subtypes. We adopt these values. So the temperature structure
of our models is described by Eq. (32)
if
of WR-winds as a function of
WR-subtypes. We adopt these values. So the temperature structure
of our models is described by Eq. (32)
if
![]() and
and
![]() where
Eq. (32) would predict a smaller value. We should point
out that the choice of
where
Eq. (32) would predict a smaller value. We should point
out that the choice of
![]() plays only a minor role in our
modeling, as most of the important physical effects occur in the
optically thick part of the wind.
plays only a minor role in our
modeling, as most of the important physical effects occur in the
optically thick part of the wind.
![]() from the demand of the momentum conservation in the wind for an
adopted velocity law. This requirement follows from Eqs.
(8) and (16):
from the demand of the momentum conservation in the wind for an
adopted velocity law. This requirement follows from Eqs.
(8) and (16):
![]() throughout the optically
thick and optically thin part of the wind. This is because the
other terms in the energy Eq. (19), i.e.
throughout the optically
thick and optically thin part of the wind. This is because the
other terms in the energy Eq. (19), i.e.
![]() and the
flow of potential, kinetic energy and enthalpy, are all very small
compared to
and the
flow of potential, kinetic energy and enthalpy, are all very small
compared to
![]() for WR-stars. So in principle we could have
used
for WR-stars. So in principle we could have
used
![]() for the calculation of
for the calculation of ![]() with Eq. (36).
In the computations we took the other terms into
account properly for the calculation of L(r). For the value of
with Eq. (36).
In the computations we took the other terms into
account properly for the calculation of L(r). For the value of
![]() in the calculation of L(r) we used the following scheme:
for the optically thick part we calculated
in the calculation of L(r) we used the following scheme:
for the optically thick part we calculated
![]() from Eq. (18)
and for the optically thin part we used
from Eq. (18)
and for the optically thin part we used
![]() ,
which is valid if
,
which is valid if
![]() (see Eq. (12)).
In any case, the exact value of
(see Eq. (12)).
In any case, the exact value of
![]() makes a difference of less
than 1 percent in the calculation of
makes a difference of less
than 1 percent in the calculation of ![]() .
.
![]() and T(r), can be expressed in terms of
the mass-loss rate and the velocity law. The velocity law in the
supersonic part of the wind is approximately a
and T(r), can be expressed in terms of
the mass-loss rate and the velocity law. The velocity law in the
supersonic part of the wind is approximately a ![]() -law:
-law:
![]() -law, only enters into our analysis for the
calculation of the velocity and density structure in the supersonic
part of the wind. For the analysis of the sonic point conditions
only the first part is important. This is equivalent to the statement
that the
-law, only enters into our analysis for the
calculation of the velocity and density structure in the supersonic
part of the wind. For the analysis of the sonic point conditions
only the first part is important. This is equivalent to the statement
that the ![]() -law does not start exactly at
-law does not start exactly at ![]() but at some
slightly larger distance where the power-law part slowly merges with
the
but at some
slightly larger distance where the power-law part slowly merges with
the ![]() -law. (In principle we could have chosen a more elaborate
expression for the velocity law that ensures a smooth transition from
the subsonic to the supersonic part, than the one adopted here,
but that would not have improved the analysis of the sonic point conditions.)
-law. (In principle we could have chosen a more elaborate
expression for the velocity law that ensures a smooth transition from
the subsonic to the supersonic part, than the one adopted here,
but that would not have improved the analysis of the sonic point conditions.)
![]() can be found from
Eq. (36). The solution of the critical point equations, which
will give the mass-loss
rate, requires knowledge of the gradients of the optical
depth and of the radiative luminosity near the sonic point.
In normal modeling of a stellar wind one would assume that
can be found from
Eq. (36). The solution of the critical point equations, which
will give the mass-loss
rate, requires knowledge of the gradients of the optical
depth and of the radiative luminosity near the sonic point.
In normal modeling of a stellar wind one would assume that
![]() is known and then solve the structure of the wind
and find the mass-loss rate. However, as argued in the introduction,
the flux-mean opacity in the atmospheres of WR-stars is not known.
Therefore, the purpose of our paper is just the opposite:
we try to find what the conditions for
is known and then solve the structure of the wind
and find the mass-loss rate. However, as argued in the introduction,
the flux-mean opacity in the atmospheres of WR-stars is not known.
Therefore, the purpose of our paper is just the opposite:
we try to find what the conditions for ![]() are that could explain
the observed mass-loss rates in terms of optically thick radiation
driven winds. A consequence of this approach is that we do not
know
are that could explain
the observed mass-loss rates in terms of optically thick radiation
driven winds. A consequence of this approach is that we do not
know ![]() ,
nor its gradient near the sonic point. Instead,
we derive it from the requirement that the model must produce the
observed mass-loss rate.
,
nor its gradient near the sonic point. Instead,
we derive it from the requirement that the model must produce the
observed mass-loss rate.
![]() from the derivative of Eq. (36) and vice versa.
Therefore we adopt two methods to estimate these gradients:
variants A and B. In the first one we make an assumption about
L(r) and find the gradient of
from the derivative of Eq. (36) and vice versa.
Therefore we adopt two methods to estimate these gradients:
variants A and B. In the first one we make an assumption about
L(r) and find the gradient of ![]() .
In variant B
we make an assumption about the variation of
.
In variant B
we make an assumption about the variation of ![]() and find the
gradient of L(r). In our modeling we will use both variants
and show that the results are quite similar. We describe these
two variants in more detail in the next section.
and find the
gradient of L(r). In our modeling we will use both variants
and show that the results are quite similar. We describe these
two variants in more detail in the next section.