WR stars usually show a whole "forest'' of iron lines in the UV shortward of
![]()
![]() (see e.g. Herald et al. 2001). One of the best studied objects among
these stars is the WC 5 star WR 111. It has already been analyzed in detail by
Hillier & Miller (1999) utilizing their line-blanketed models. Therefore it shall also serve here as
the prototype for a first application of our code, examining the effects of line-blanketing.
(see e.g. Herald et al. 2001). One of the best studied objects among
these stars is the WC 5 star WR 111. It has already been analyzed in detail by
Hillier & Miller (1999) utilizing their line-blanketed models. Therefore it shall also serve here as
the prototype for a first application of our code, examining the effects of line-blanketing.
In the present section we present a model for WR 111 with solar iron abundance and compare it to a similar model with zero iron abundance. The model calculations are described in Sect. 4.1, and the results are discussed with regard to the emergent flux distribution (Sect. 4.2), the ionization stratification (Sect. 4.3), and the wind dynamics (Sect. 4.4).
![\begin{figure}
\par\includegraphics[width=15.7cm,clip]{h3177f3.ps}\end{figure}](/articles/aa/full/2002/19/aah3177/Timg150.gif) |
Figure 3:
Spectral fit for WR 111. The observation (thin line) is shown together
with the synthetic spectrum (thick line). The model parameters are compiled in
Table 3. Prominent spectral lines are identified. The observed flux has been
divided by the reddened model continuum for normalization. A correction for interstellar
Ly |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
| D | 10 |
|
|
|
|
|
|
| 0.45 | |
| 0.04 | |
|
|
|
|
|
|
| M - m |
|
| EB-V |
|
|
|
Observational data for WR 111 are retrieved from the following sources. The UV data are from the IUE satellite, retrieved from the INES database (http://ines.vilspa.esa.es). Optical spectra come from the atlas of Torres & Massey (1987). In addition, optical narrow-band colors (b, v) from Lundström & Stenholm (1984) are considered. Infrared continuum fluxes are given by Eenens & Williams (1992), obtained from broad-band photometry and corrected for the contribution of emission lines. The line-blanketed model spectrum is compared to the observations in Fig. 3 (lines), Fig. 4 (flux distribution in the UV and optical) and Fig. 6 (IR and optical photometry).
For the spectral analysis the mass fractions of silicon and iron are set to solar values and a
distance modulus of 11.0 mag is adopted, which corresponds to a distance of 1.58 kpc
(see discussion in Hillier & Miller 1999). The Doppler broadening velocity is set to
![]() which reproduces well the blue shifted absorptions of P-Cygni type line profiles. The
density contrast D (clumping) is estimated by fitting the line wings of highly excited ions
(He II and C IV). The value of D=10, which reduces the derived mass loss rates by a
factor of
which reproduces well the blue shifted absorptions of P-Cygni type line profiles. The
density contrast D (clumping) is estimated by fitting the line wings of highly excited ions
(He II and C IV). The value of D=10, which reduces the derived mass loss rates by a
factor of ![]() ,
is commonly accepted for early-type WC stars
(Hillier 1996; Hamann & Koesterke 1998; Hillier & Miller 1999).
,
is commonly accepted for early-type WC stars
(Hillier 1996; Hamann & Koesterke 1998; Hillier & Miller 1999).
The C III/C IV ionization structure is determined by means of spectral lines of C III (e.g.
1620, 1923, 2010, 2297, 4650, 5696 and 6750 Å) versus C IV (e.g. 2405, 2525, 2595, 2699
and 5812 Å). These lines are reproduced well, except for C III 2297 Å (which
is mainly fed by dielectronic recombination) and the classification line C III 5696 Å.
Simultaneously, the ratio
![]() is derived from the neighboring lines
He II/C IV 5412/5470 Å, the He II lines at 1640, 2734 and 3204 Å, and the He II
Pickering series.
is derived from the neighboring lines
He II/C IV 5412/5470 Å, the He II lines at 1640, 2734 and 3204 Å, and the He II
Pickering series.
For the determination of the oxygen mass fraction ![]() ,
ionization stages O III to O V
(O III 3120, 3270, 3961 Å, the O III/O IV/C IV complex around 3700 Å, O III/O VI at
5270 Å, O III/O V at 5590 Å, O IV 3070 and 3410 Å, and O V at 3146 and 5114 Å)
are used. Most of these lines fit very well, except O III 3120 and 3961 Å. One of these two
lines, O III 3120 Å, is a Bowen emission line (Bowen 1935), i.e. it shares a common
upper level with O III 303.6 Å, and is therefore pumped by interaction with the He II
resonance line at 303.8 Å. As demonstrated by Schmutz (1997), this effect is sensitive to
the value of the He II 303.8 profile function at the frequency of the O III 303.6 blend. The
difficulties with O III 3120 Å may therefore arise from the simplified treatment of line
broadening by pure Doppler profiles.
,
ionization stages O III to O V
(O III 3120, 3270, 3961 Å, the O III/O IV/C IV complex around 3700 Å, O III/O VI at
5270 Å, O III/O V at 5590 Å, O IV 3070 and 3410 Å, and O V at 3146 and 5114 Å)
are used. Most of these lines fit very well, except O III 3120 and 3961 Å. One of these two
lines, O III 3120 Å, is a Bowen emission line (Bowen 1935), i.e. it shares a common
upper level with O III 303.6 Å, and is therefore pumped by interaction with the He II
resonance line at 303.8 Å. As demonstrated by Schmutz (1997), this effect is sensitive to
the value of the He II 303.8 profile function at the frequency of the O III 303.6 blend. The
difficulties with O III 3120 Å may therefore arise from the simplified treatment of line
broadening by pure Doppler profiles.
The O VI lines at 3811 and 5270 Å are not reproduced simultaneously with C III. A similar discrepancy is already known for the O VI resonance line in O-star atmospheres. For O-stars, it can be resolved by the inclusion of an additional X-ray emissivity from shock heated material (Pauldrach et al. 1994). Preliminary model calculations show evidence, that the inclusion of an X-ray emission according to Raymond & Smith (1977) has significant influence on the O VI lines in WC stars. If already marginally visible in the emergent spectrum, these lines can be strengthened by a factor of about two.
The derived model parameters are listed in Table 3. Compared to the work of
Hillier & Miller we obtain similar values for the stellar temperature ![]() (85 kK vs.
90 kK), the terminal wind velocity
(85 kK vs.
90 kK), the terminal wind velocity ![]() (2200 km s-1 vs. 2300 km s-1), the clumping factor
D=10, and the carbon mass fraction
(2200 km s-1 vs. 2300 km s-1), the clumping factor
D=10, and the carbon mass fraction
![]() ,
whereas we find a considerably lower
oxygen mass fraction (
,
whereas we find a considerably lower
oxygen mass fraction (
![]() vs. 0.15), and a higher luminosity (
vs. 0.15), and a higher luminosity (
![]() vs.
vs.
![]() ).
).
For a comparison of the derived mass loss rates (
![]() vs.
vs.
![]() )
it is necessary to consider the different luminosities of both models.
From Eq. (3) follows that the spectroscopic mass loss rates scale as
)
it is necessary to consider the different luminosities of both models.
From Eq. (3) follows that the spectroscopic mass loss rates scale as
![]() ,
i.e. our value of
,
i.e. our value of
![]() would scale
down to a considerably lower value of
would scale
down to a considerably lower value of
![]() for a luminosity of
for a luminosity of
![]() and
and
![]() .
.
As shown in Fig. 4 the emergent flux of our model reproduces very well the
observed energy distribution in the optical and UV spectral range. In the infrared
(Fig. 6) the measured continuum fluxes of Eenens & Williams (1992) lie about
0.1 dex above the model flux. Because Hillier & Miller use a lower reddening parameter, they
encounter an even higher discrepancy in the infrared (![]()
![]() ), and resolve
it through the application of a non-standard extinction law (Cardelli et al. 1988).
), and resolve
it through the application of a non-standard extinction law (Cardelli et al. 1988).
As recognized first by Koenigsberger & Auer (1985), the "iron forest'' of emission and absorption lines of
Fe IV, Fe V and Fe VI forms a pseudo continuum below ![]()
![]() (see
Fig. 4). The blanketed model spectra therefore show a steeper apparent
continuum slope in the UV. Consequently, a higher reddening parameter - with respect to
un-blanketed models - must be adopted to reproduce the observed flux distribution. As a result
the derived stellar luminosity is increased. On the other hand the flux in the far UV is
blocked by iron lines, and is redistributed to the UV (see Fig. 5), which
leads to lower derived luminosities. In total, recent studies (Crowther et al. 2000; Dessart et al. 2000) show a
trend to derive higher luminosities for WC stars when line-blanketed models are applied.
(see
Fig. 4). The blanketed model spectra therefore show a steeper apparent
continuum slope in the UV. Consequently, a higher reddening parameter - with respect to
un-blanketed models - must be adopted to reproduce the observed flux distribution. As a result
the derived stellar luminosity is increased. On the other hand the flux in the far UV is
blocked by iron lines, and is redistributed to the UV (see Fig. 5), which
leads to lower derived luminosities. In total, recent studies (Crowther et al. 2000; Dessart et al. 2000) show a
trend to derive higher luminosities for WC stars when line-blanketed models are applied.
In the present work we derive values of
![]() and
EB-V=0.325 mag
for WR 111 using the standard extinction law of Seaton (1979). Hillier & Miller derive a
lower luminosity of
and
EB-V=0.325 mag
for WR 111 using the standard extinction law of Seaton (1979). Hillier & Miller derive a
lower luminosity of
![]() with
EB-V = 0.30 mag, and Koesterke & Hamann (1995)
deduce a luminosity of
with
EB-V = 0.30 mag, and Koesterke & Hamann (1995)
deduce a luminosity of
![]() with
EB-V = 0.25 mag based on
un-blanketed models. Obviously, the derived luminosity depends on the treatment of iron group
line-blanketing, as it affects the emergent flux distribution considerably. In addition,
uncertainties arise from the interstellar extinction law. In the UV below
with
EB-V = 0.25 mag based on
un-blanketed models. Obviously, the derived luminosity depends on the treatment of iron group
line-blanketing, as it affects the emergent flux distribution considerably. In addition,
uncertainties arise from the interstellar extinction law. In the UV below ![]()
![]() the extinction law of Cardelli et al. (1988) applied by Hillier & Miller shows
substantial differences compared with Seaton (1979).
the extinction law of Cardelli et al. (1988) applied by Hillier & Miller shows
substantial differences compared with Seaton (1979).
The ionizing fluxes from our model compare very well to the blanketed model of
Hillier & Miller (as listed in Dessart et al. 2000) after a scaling by 0.15 dex due to the
difference in luminosity is performed. For the number of Lyman continuum photons we obtain a
value of
![]() compared to
compared to
![]() from
Hillier & Miller, and for the number of He I photons we get a slightly higher value of
from
Hillier & Miller, and for the number of He I photons we get a slightly higher value of
![]() compared to
compared to
![]() .
The comparison to our
un-blanketed model shows that line blanketing diminishes the number of He I photons by
0.26 dex (compared to
.
The comparison to our
un-blanketed model shows that line blanketing diminishes the number of He I photons by
0.26 dex (compared to
![]() for the un-blanketed model), whereas the
number of Lyman continuum photons is nearly unaffected (
for the un-blanketed model), whereas the
number of Lyman continuum photons is nearly unaffected (
![]() vs.
vs.
![]() ). The small discrepancy in the number of He I photons compared
to Hillier & Miller might be explained by the different oxygen abundances.
). The small discrepancy in the number of He I photons compared
to Hillier & Miller might be explained by the different oxygen abundances.
In Fig. 7 the ionization stratification of the blanketed model is compared to
its un-blanketed counterpart. The most striking effect of line-blanketing is the enhanced
recombination from C IV to C III in the outer part of the wind, where the
population of the C III ground state is increased from ![]() 10-3 up to
10-3 up to ![]() 1.
The emergent C III line emissions are strengthened by a factor of
1.
The emergent C III line emissions are strengthened by a factor of ![]() 2 (with strong
scatter) compared to the un-blanketed model. The other ions are also affected, but the
corresponding changes are of minor importance for the spectral appearance of the models.
2 (with strong
scatter) compared to the un-blanketed model. The other ions are also affected, but the
corresponding changes are of minor importance for the spectral appearance of the models.
Because the line emission of WR stars is dominated by recombination processes, the emission line intensity is basically a measure for the wind density and therefore also for the mass loss rate. For this reason the enhanced recombination leads to a reduction of the derived mass loss rates.
In the outer part of the wind the electron temperature is only marginally changed (cf. Fig. 8). The back warming effect, which results from the increase of the Rosseland mean opacity, appears in the optically thick part of the envelope. In these layers the temperature is increased by about 20% without effect on the model spectrum. The changes in ionization result from very complex radiative interactions between the different ions. Therefore the various effects can not be clearly separated. Nevertheless, a closer inspection allows some interpretations.
The ionization from C III to C IV is strongly influenced by shading effects. At the
relevant depth the radiation field below ![]() 320 Å is effectively blocked by a large
number of iron group lines. Therefore the ionization of C III (ionization edge at
258 Å) is strongly reduced. Test calculations show that the ionization stratification of
carbon changes significantly if only iron line-blanketing is accounted for and the rest of the
iron group elements is omitted. Probably this effect is responsible for the higher mass loss
rate derived by Hillier & Miller. Because these authors do not account for the whole iron group
they obtain a weaker recombination which is compensated by a higher wind density.
320 Å is effectively blocked by a large
number of iron group lines. Therefore the ionization of C III (ionization edge at
258 Å) is strongly reduced. Test calculations show that the ionization stratification of
carbon changes significantly if only iron line-blanketing is accounted for and the rest of the
iron group elements is omitted. Probably this effect is responsible for the higher mass loss
rate derived by Hillier & Miller. Because these authors do not account for the whole iron group
they obtain a weaker recombination which is compensated by a higher wind density.
Obviously the inclusion of the complete iron group is of some importance, but the simplified treatment as one generic element is a questionable approximation. Especially, different ionization and excitation conditions may result when the detailed atomic models are accounted for separately. The splitting of the iron group into different model atoms will therefore be a subject of our future work.
The main ionization stages of iron in the outer envelope are Fe V and Fe VI with ionization
edges at 165 Å and 128 Å. In the regions where He II or C IV with edges at
228 Å and 192 Å are the leading ions, the ionization of iron is only possible from
highly excited energy levels. Actually this is the case because of the metastable nature of the
low lying iron levels (cf. Sect. 3.1). From Fig. 1 it can
be seen that for Fe V the levels up to ![]() 1/3 of the ionization energy are of same
parity, and are therefore supporting the ionization of Fe V.
1/3 of the ionization energy are of same
parity, and are therefore supporting the ionization of Fe V.
For a radiation driven wind, the average number of scatterings before a photon escapes from the
atmosphere is indicated by the wind efficiency
![]() .
In
former model calculations for WC stars values of
.
In
former model calculations for WC stars values of
![]() are derived
(Koesterke & Hamann 1995; Gräfener et al. 1998). Even though multiple photon scattering might be efficient in spectral
regions with a very high line density, these high values led to the question if the mass loss
of WR stars can be driven by radiation pressure alone.
are derived
(Koesterke & Hamann 1995; Gräfener et al. 1998). Even though multiple photon scattering might be efficient in spectral
regions with a very high line density, these high values led to the question if the mass loss
of WR stars can be driven by radiation pressure alone.
For the current WR models this situation has changed, because lower mass loss rates are derived
by accounting for clumping, and higher luminosities are predicted by line-blanketed models.
Both effects lead to lower values for the wind efficiency ![]() .
In the present work we
obtain a value of
.
In the present work we
obtain a value of
![]() for WR 111. This value even lies below the wind efficiencies
calculated by Springmann & Puls (1998) in their Monte-Carlo simulations. Therefore, the mass loss of
WR 111 seems to be easily explicable by radiative driving.
for WR 111. This value even lies below the wind efficiencies
calculated by Springmann & Puls (1998) in their Monte-Carlo simulations. Therefore, the mass loss of
WR 111 seems to be easily explicable by radiative driving.
In our radiation transport calculations, the radiative acceleration
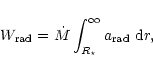 |
(43) |
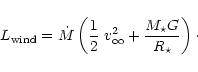 |
(44) |
![\begin{figure}
\par\includegraphics[width=8.8cm,clip]{h3177f9.ps}\end{figure}](/articles/aa/full/2002/19/aah3177/Timg204.gif) |
Figure 9:
Acceleration in units of the local gravity, as function of radius. The wind acceleration
|
Copyright ESO 2002