| Element X | Z |
|
| Sc | 21 |
|
| Ti | 22 |
|
| V | 23 |
|
| Cr | 24 |
|
| Mn | 25 |
|
| Fe | 26 | 1.0 |
| Co | 27 |
|
| Ni | 28 |
|
The numerical solution of the statistical equations is limited to model atoms with a few hundred energy levels. However, the complex electron configurations of the iron group elements would require thousands of energy levels for a detailed description. For this reason, a simplified treatment is necessary. In the present work we adopt the concept of super-levels, which has originally been proposed by Anderson (1989).
In this approximation a large number of atomic energy levels (termed "sub-levels'' in the following) is represented by a small number of "super-levels''. Each transition between two super-levels comprises a large number of atomic line transitions ("sub-lines''). In the radiation transport, all sub-lines must be treated at their proper frequency because of the frequency coupling in expanding atmospheres. So in contrast to static atmospheres, no sampling or re-ordering techniques can be applied. Instead, each super-line has a complicated "profile function'' which is a superposition of all sub-lines involved.
The preparation of the model atom and the transition cross sections in the present work is based on the work of Dreizler & Werner (1993). The complete iron group data of Kurucz (1991), with some 107 line transitions between several thousands of energy levels, are represented by model atoms with 10-20 super-levels per ionization stage.
In the following, we describe the construction of the model atom (Sect. 3.1), the representation of opacities and emissivities in the radiation transport (Sect. 3.2), and the corresponding transition probabilities in the statistical equations (Sect. 3.3).
| Element X | Z |
|
| Sc | 21 |
|
| Ti | 22 |
|
| V | 23 |
|
| Cr | 24 |
|
| Mn | 25 |
|
| Fe | 26 | 1.0 |
| Co | 27 |
|
| Ni | 28 |
|
For the construction of the model atom, the atomic energy levels from the Kurucz data (Kurucz 1991) are divided into energy bands BL, each of which is represented by a super-level L. The relative occupation of the sub-levels whithin each energy band is assumed to be in LTE, corresponding to a temperature T. In the present section we do not specify this temperature and work out the expressions for the super-level energies and statistical weights for the general case (in Sect. 3.2 we will give a detailed discussion of this point).
Owing to the similarities in the electron configurations, it is even possible to represent the whole iron group by one generic model atom (Dreizler & Werner 1993; Haas et al. 1996). In this case, the energy levels of different elements i are weighted corresponding to their relative abundances ai(Table 2). The advantage of this approach is the computationally cheap consideration of all important iron group opacities. The disadvantage is the loss of accuracy concerning the modeling of the detailed atomic processes.
Under the assumption of LTE, the relative occupation of the sub-levels within an
energy band is
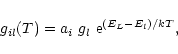 |
(15) |
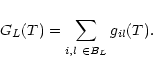 |
(16) |
| EL(T) | = | 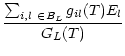 |
|
| = | 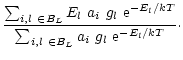 |
(17) |
For a sub-line between sub-levels l and u the opacity ![]() and emissivity
and emissivity ![]() are
given by
are
given by
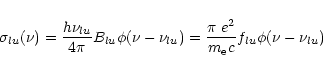 |
(21) |
The opacities and emissivities for transitions between super-levels ("super-lines'') are
obtained by adding up the opacities and emissivities of the involved sub-lines. For given
super-level populations nL and nU the sub-level populations nl and nu are
calculated from Eq. (18), and we obtain
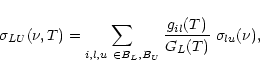 |
(24) |
Note that the energies, statistical weights and cross sections for super-levels and super-lines
depend on the temperature T, which has not yet been specified. Due to the large number of
spectral lines accounted for (![]() 107), a relatively large amount of computing time is
needed for the calculation of the
107), a relatively large amount of computing time is
needed for the calculation of the
![]() .
Therefore, we calculate the
.
Therefore, we calculate the
![]() ,
EL and GL in advance to the atmosphere calculations for fixed excitation temperatures.
By this, we also avoid to handle the super-level energies, statistical weights and composite
cross sections as being dependent on temperature and hence on radius. In our subsequent
notation we will omit the explicit temperature dependences in these expressions.
,
EL and GL in advance to the atmosphere calculations for fixed excitation temperatures.
By this, we also avoid to handle the super-level energies, statistical weights and composite
cross sections as being dependent on temperature and hence on radius. In our subsequent
notation we will omit the explicit temperature dependences in these expressions.
The excitation temperatures are chosen as a typical ionization temperature for each
ion. Starting from values obtained from the Saha equation for typical densities, they are
iterated in the present work to match the local electron temperature ![]() for the main
ionization stages of the model presented in Sect. 4. The exact choice of the
excitation temperatures turned out not to be critical.
for the main
ionization stages of the model presented in Sect. 4. The exact choice of the
excitation temperatures turned out not to be critical.
With T set to a fixed excitation temperature, the direct application of
Eqs. (22) and (23) is not possible anymore, because in the
LTE-limit the line source function
![]() does not match the Planck
function
does not match the Planck
function
![]() ,
which would lead to severe problems at large depth. We
circumvent these problems by inserting the local electron temperature
,
which would lead to severe problems at large depth. We
circumvent these problems by inserting the local electron temperature ![]() into the
exponential terms in these equations, i.e. the EL, GL and
into the
exponential terms in these equations, i.e. the EL, GL and
![]() are evaluated
for the excitation temperature T, but
are evaluated
for the excitation temperature T, but
![]() and
and ![]() remain compatible to
remain compatible to
![]()
Hence our super-level treatment implies the following approximations: (1) relative population
numbers within each super-level according to Boltzmann's formula (LTE), (2) evaluation of these
relative population numbers with an approximate temperature, (3) neglect of lines between
sub-levels within the same super-level. Clearly, the higher the number of super-levels, i.e.
the smaller their energy bandwidth, the less is the error. Note that the approximations affect
the way how the atomic cross sections are combined, but do not introduce any inconsistencies.
![\begin{figure}
\par\includegraphics[width=8.8cm,clip]{h3177f2.ps}\end{figure}](/articles/aa/full/2002/19/aah3177/Timg125.gif) |
Figure 2:
Super-line cross section
|
In analogy to the lines, the continuum cross sections of the iron group elements are also added
up to a composed cross section for each super level. If available, data from the Opacity
Project (Seaton et al. 1992; Cunto & Mendoza 1992) are used. Otherwise the continua are treated in hydrogenic
approximation under the assumption of an effective principal quantum number
The radiative rate coefficients are calculated consistently to the opacities and emissivities
in Eqs. (26) and (27) by dividing the terms under the integral by
![]() in oder to convert energies into photon numbers. For spontaneous emission processes we
get from Eq. (27)
in oder to convert energies into photon numbers. For spontaneous emission processes we
get from Eq. (27)
For that purpose, we define effective Einstein coefficients AUL, mean intensities
![]() ,
and their derivatives
,
and their derivatives
![]() .
The
rate integrals (Eqs. (30), (31), and (32)) are
simplified by substituting
.
The
rate integrals (Eqs. (30), (31), and (32)) are
simplified by substituting ![]() by the mean frequency
by the mean frequency ![]() (Eq. (25)) in all
slowly varying terms (i.e. except in
(Eq. (25)) in all
slowly varying terms (i.e. except in ![]() and
and
![]() ). Because the cross
sections have a limited bandwidth, in most cases with a pronounced maximum around
). Because the cross
sections have a limited bandwidth, in most cases with a pronounced maximum around ![]() ,
this substitution does not affect the rate coefficients considerably. The approximate rate
coefficients are
,
this substitution does not affect the rate coefficients considerably. The approximate rate
coefficients are
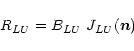 |
(33) |
 |
(34) |
Collisional cross sections are calculated by application of the generalized formula of van Regemorter (1962) to the effective Einstein coefficients AUL (Eq. (35)).
Copyright ESO 2002