For the calculations of the Stokes parameters of the scattered line, the magnetic field vector is defined by its strength B, by the polar angle ![]() with the polar axis, and by the azimuthal angle
with the polar axis, and by the azimuthal angle ![]() between the solar limb tangent (Px) and the projection of the magnetic field vector on the plane (xPy) tangent to the solar limb.
between the solar limb tangent (Px) and the projection of the magnetic field vector on the plane (xPy) tangent to the solar limb.
In the comoving frame, the atom absorbs the incident radiation at the transition frequency
![]() (we assume that the absorption profile is a
(we assume that the absorption profile is a ![]() -function). However in the laboratory frame, the moving atom, with a velocity vector
-function). However in the laboratory frame, the moving atom, with a velocity vector
![]() ,
absorbs the incident radiation coming from a given elementary area around a point M on the spherical cap at the shifted frequency
,
absorbs the incident radiation coming from a given elementary area around a point M on the spherical cap at the shifted frequency
![]() .
.
![]() is the unitary vector of the direction
is the unitary vector of the direction
![]() of angular coordinates
of angular coordinates
![]() in the solar frame (Pxyz).
We note by
in the solar frame (Pxyz).
We note by
![]() the angular distribution of the local intensity at the scattering point P for the radiation coming from the direction
the angular distribution of the local intensity at the scattering point P for the radiation coming from the direction
![]() at the frequency
at the frequency ![]() (given in erg cm-2 s-1 sr-1 Hz-1).
(given in erg cm-2 s-1 sr-1 Hz-1).
We denote the polarization matrix of the incident photons at the frequency ![]() by
by
![]() ,
which depends on the frequency because of the scattering atom motion. This matrix is obtained by averaging the incident radiation on all the directions (Sahal-Bréchot et al. 1998). It should be normalized to the mean local intensity of the incident radiation
,
which depends on the frequency because of the scattering atom motion. This matrix is obtained by averaging the incident radiation on all the directions (Sahal-Bréchot et al. 1998). It should be normalized to the mean local intensity of the incident radiation
Equation (3) implies that the polarization matrix of the incident radiation can be written as the angular average
![]() multiplied by a unitary matrix
multiplied by a unitary matrix
![]() ,
which describes the angular behavior of the incident radiation coming in the direction
,
which describes the angular behavior of the incident radiation coming in the direction
![]() (for more details see Sahal-Bréchot et al. 1998). The elements of the polarization matrix expanded on the irreducible tensor basis
(for more details see Sahal-Bréchot et al. 1998). The elements of the polarization matrix expanded on the irreducible tensor basis
![]() are obtained by expanding the matrix
are obtained by expanding the matrix
![]() in multipole terms on the same basis in the solar frame (Pxyz) ((Pz) is the quantization axis), thus
in multipole terms on the same basis in the solar frame (Pxyz) ((Pz) is the quantization axis), thus
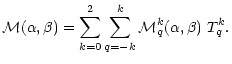 |
(4) |
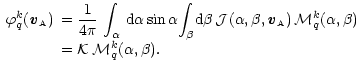 |
(5) |
The density matrix of an atom in interaction with its surrounding medium (incident photons and colliding particles) depends on the local magnetic field and eventually on the atomic velocity field. It is more practical to write the equations describing this interaction in the frame where the magnetic field vector is parallel to the quantization axis. This permits to keep the magnetic quantum number as a good quantum number. In addition, the density matrix elements of the reemitted photons are easily obtained in this frame.
We note by
![]() the magnetic frame, the quantization axis
the magnetic frame, the quantization axis
![]() is parallel to the magnetic field vector. It is, so, necessary to rewrite the density matrix elements of the incident photons in the frame
is parallel to the magnetic field vector. It is, so, necessary to rewrite the density matrix elements of the incident photons in the frame
![]() which is obtained from the solar one (Pxyz) by a rotation with the Euler angle
which is obtained from the solar one (Pxyz) by a rotation with the Euler angle
![]() (
(![]() and
and ![]() are respectively the azimuth and the polar angle of the magnetic field vector in the frame (Pxyz)).
are respectively the azimuth and the polar angle of the magnetic field vector in the frame (Pxyz)).
The formula giving the density matrix elements
![]() (relative to a frame
(relative to a frame
![]() )
obtained from the elements
)
obtained from the elements
![]() (relative to a frame
(relative to a frame ![]() )
through a rotation from
)
through a rotation from ![]() to
to
![]() of angles
of angles
![]() is given by (Bommier 1977)
is given by (Bommier 1977)
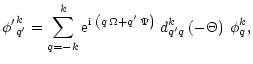 |
(6) |
We note by
![]() the incident photons density matrix in
the incident photons density matrix in
![]() .
The matrix elements of
.
The matrix elements of
![]() are obtained from those of
are obtained from those of
![]() by using the equation of the density matrix element transformation by an Euler rotation given by
by using the equation of the density matrix element transformation by an Euler rotation given by
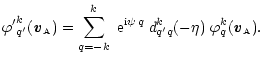 |
(7) |
![\begin{eqnarray*}\begin{array}{l}
{\varphi^\prime}^0_0({\textbf{\textit{v}}}_{\s...
...f{\textit{v}}}_{\scriptscriptstyle{\rm {A}}})\right]
\end{array}\end{eqnarray*}](/articles/aa/full/2002/17/aa1681/img72.gif)
![$\displaystyle \begin{array}{l}
{\varphi^\prime}^2_1({\textbf{\textit{v}}}_{\scr...
...phi^2_2({\textbf{\textit{v}}}_{\scriptscriptstyle{\rm {A}}})\right]
\end{array}$](/articles/aa/full/2002/17/aa1681/img73.gif) |
(8) |
![\begin{eqnarray*}\begin{array}{l}
{\varphi^\prime}^2_2({\textbf{\textit{v}}}_{\s...
...f{\textit{v}}}_{\scriptscriptstyle{\rm {A}}})\right].
\end{array}\end{eqnarray*}](/articles/aa/full/2002/17/aa1681/img74.gif)
| (9) |
As mentioned in Sahal-Bréchot et al. (1998), the expressions obtained for the polarization matrix elements of the incident radiation are general and no restricting assumptions are made to this part. In order to get the density matrix of the reemitted photons which lead to the Stokes parameters of the scattered radiation, we should write and solve the statistical equilibrium equations describing the interaction of the moving atom with the incident radiation.
Copyright ESO 2002