The aim of the present work is to determine the equations giving the Stokes parameters of a resonance scattered spectral line by moving atoms in the presence of a local magnetic field. The scattered line is supposed to be sensitive simultaneously to the Hanle effect due the local magnetic field and to the Doppler redistribution effect due the macroscopic velocity field of the scattering atoms. These atoms are supposed to be excited by isotropic collisions and by a partially anisotropic radiation field. Owing to this partial anisotropy, the scattered photons are linearly and partially polarized. This is the case of the coronal ions which scatter the partially anisotropic radiation coming from the underlying chromosphere-corona transition region.
The physical system considered is composed of moving atoms in an elementary volume located at P (theoretically, one point: Fig. 3). The scattering volume is located at a given distance above the limb. The incident unpolarized photons come from a spherical cap on the Sun, limited by the cone tangent to the Sun and with vertex at the point P. The atoms interact with the local magnetic field embedded in the surrounding medium. This is the case of the coronal ions, such as O VI, which absorb and reemit by resonance scattering the unpolarized radiation coming from the underlying transition region. The scattered photons are observed in the direction of the line of sight which makes an angle ![]() (scattering angle) with the vertical to the Sun which is the symmetry axis of the incident radiation cone.
(scattering angle) with the vertical to the Sun which is the symmetry axis of the incident radiation cone.
Hereafter, we adopt the model of the two-level atom which is valid for the description of the scattered radiation by the coronal ions in the EUV wavelength domain. We assume that the lower level of the atomic transition considered is not polarizable (which is the case of the lower level of the
![]() transition of the O VI D2 coronal line). The electrons velocity field distribution is an isotropic Maxwellian, so the electronic collisions do not create atomic polarization (i.e., population imbalance) in the upper level of the atomic transition.
transition of the O VI D2 coronal line). The electrons velocity field distribution is an isotropic Maxwellian, so the electronic collisions do not create atomic polarization (i.e., population imbalance) in the upper level of the atomic transition.
Atoms interact with photons and colliding particles (electrons) independently. Studying the interaction of one atom with the local medium leads to the statistical equilibrium equations where the solutions are the populations and coherences between the Zeeman sublevels which are related to the Stokes parameters of the scattered photons. To obtain solutions (Stokes parameters) of the whole system at a given frequency, we then can sum the obtained solutions for one atom over all the atoms of the system, having the same velocity field along the line of sight. Hereafter we will consider only one scattering atom for the computations of the Stokes parameters of the scattered photons as a function of the magnetic field and the atoms macroscopic velocity field vectors. At the end, we will sum the final results over the atoms of the whole system (for more details, see Sahal-Bréchot et al. 1998).
The total system (scattering atom, colliding particles, radiation and magnetic field) is isolated and reversible. So, it can be described by its density matrix, ![]() ,
solution of the Schrödinger equation
,
solution of the Schrödinger equation
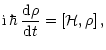 |
(2) |
Copyright ESO 2002