5 Atom-radiation interaction: Atomic density matrix

We denote with $\rho_{\scriptscriptstyle{\rm {A}}}\left({\textbf{\textit{v}}}_{\scriptscriptstyle{\rm {A}}},t\right)$ the density matrix of an atom having the velocity vector ${\textbf{\textit{v}}}_{\scriptscriptstyle{\rm {A}}}$. We have

$$\int {\rm Tr}_{\scriptscriptstyle{\rm {A}}}\left[ \rho_{\scriptsc... ...d}}^{^{\scriptstyle{3}}} {\textbf{\textit{v}}}_{\scriptscriptstyle{\rm {A}}}=1,$$ (10)

because the trace of $\rho_{\scriptscriptstyle{\rm {A}}}\left({\textbf{\textit{v}}}_{\scriptscriptstyle{\rm {A}}},t\right)$ is the sum of level populations of an atom with a velocity vector ${\textbf{\textit{v}}}_{\scriptscriptstyle{\rm {A}}}$.

In order to obtain, in the laboratory frame, the master equation for $\rho_{\scriptscriptstyle{\rm {A}}}\left({\textbf{\textit{v}}}_{\scriptscriptstyle{\rm {A}}},t\right)$, which describes the evolution of the atomic subsystem coupled with its surrounding medium (photons and colliding particles (electrons)) (Bommier & Sahal-Bréchot 1978; Cohen-Tannoudji 1962 & 1977; Fano 1957), we assume few approximations. The impact approximation (Bommier & Sahal-Bréchot 1991) supposes that the mean duration of the atom interaction with a photon or an electron is much shorter than the mean duration separating two successive interactions; the "no-back reaction'' approximation (Bommier & Sahal-Bréchot 1991; Cohen-Tannoudji 1977; Cohen-Tannoudji et al. 1988; Fano 1957), also supposes that the atom surrounding medium has enough degrees of freedom to dissipate rapidly the atom interaction effects in the way that they will not have any back effect on this atom; the Markovian evolution of $\rho_{\scriptscriptstyle{\rm {A}}}\left({\textbf{\textit{v}}}_{\scriptscriptstyle{\rm {A}}},t\right)$ supposes that this evolution depends only on the present time. We neglect also the atom recul during the interaction with the electrons, this is because of the atom-electron mass ratio. It is also the case for the atom-photon interaction.

The complete equation for the atomic density matrix evolution is given by Eq. (36) in Bommier & Sahal-Bréchot (1978). By taking into account the approximations cited previously, the master equation of the atomic subsystem density matrix takes the following form

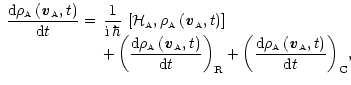$$\begin{array}{ll} {\displaystyle \frac{{\rm {d}}\rho_{\scriptscri... ...riptscriptstyle{\rm {A}}},t\right)} {{\rm {d}}t}\right)_{\rm {C}}}, \end{array}$$ (11)

where the indexes ${\rm R}$ and ${\rm C}$ are respectively relative to the photons subsystem and to the colliding particles one. They represent an average on the states of the two subsystems photons and colliding particles, which are completely decoupled.

Writing the coupling terms of the master equation as a function of the corresponding S matrixes (scattering matrixes) (see Bommier & Sahal-Bréchot 1991) permits us to compute them easily. The atom interaction with the electrons with a isotropic distribution affects only the Zeeman sub-level populations. The atom motion appears only in the coupling terms with the incident photons, whose density matrix elements were computed previously.

In the case of a two-level atom (e.g. the case of the O VI D₂ coronal line), we obtain the statistical equilibrium equations between the upper level u and the lower level l of the atomic transition considered. In the irreducible tensor basis, by taking into account of the magnetic-field effect and of the atom velocity-field effect (the quantization axis is parallel to the magnetic field vector), we obtain in the frame $(PX^{\prime}Y^{\prime}Z^{\prime})$

$$\begin{array}{l} {\displaystyle ^{J_{\rm u}J_{\rm u}}{\rho_{\... ...J_{\rm u} & J_{\rm l} \end{array}\right\} \Bigg] }, \end{array}$$ (12)

where $\omega$ is the Larmor frequency and $\alpha_{\rm lu}\left(T_{{\rm e}}\right)$ is the electron excitation rate. k=0 or 2 in this case. The term with k=0 (q=0) gives the upper level population and the other terms with k=2 $(q=0;\pm1;\pm2)$ are related to the linear polarization parameters of the atomic transition (alignment terms). $\varphi^\prime$ is the polarization matrix of the incident photons in the magnetic frame $(PX^{\prime}Y^{\prime}Z^{\prime})$ ($\varphi$ in the solar frame (Pxyz)).