The polarization matrix elements of the reemitted photons can be obtained from the previous equation describing the evolution of the atomic subsystem in interaction with the incident photons and the colliding particles in the presence of a magnetic field. We denote by
![]() this matrix in the magnetic field frame
this matrix in the magnetic field frame
![]() where the quantization axis
where the quantization axis
![]() is parallel to the magnetic field vector. The polarization matrix elements
is parallel to the magnetic field vector. The polarization matrix elements
![]() of the reemitted photons are given (as number of re-emitted photons per unit time, per unit volume and per unit velocity distribution) by
of the reemitted photons are given (as number of re-emitted photons per unit time, per unit volume and per unit velocity distribution) by
![\begin{displaymath}\begin{array}{l}
{\displaystyle
\phi_{q}^{k}
\left({\textbf{...
...riptscriptstyle{\rm {A}}}\right) }
\; c(k) \Bigg],
\end{array}\end{displaymath}](/articles/aa/full/2002/17/aa1681/img93.gif) |
(13) |
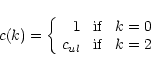 |
(14) |
Then, the polarization matrix elements of the reemitted photons written in the frame of the magnetic field are given by
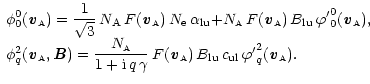 |
(15) |
| (16) |
It is more useful to rewrite these polarization matrix elements of the reemitted radiation first in the solar frame (Pxyz) and then in the frame of the line of sight (PXYZ). This is to reduce the number of rotation angles in the final expressions. The atomic frame (Pxyz) is obtained from the magnetic frame
![]() by a rotation with angles
by a rotation with angles
![]() .
We note with
.
We note with
![]() and
and
![]() ,
respectively, the polarization matrix elements of the scattered photons (developed on the irreducible tensor basis) in the solar frame (Pxyz) and in the frame of the line of sight (PXYZ).
,
respectively, the polarization matrix elements of the scattered photons (developed on the irreducible tensor basis) in the solar frame (Pxyz) and in the frame of the line of sight (PXYZ).
The polarization matrix elements of the reemitted photons
![]() written in (Pxyz) are given by
written in (Pxyz) are given by
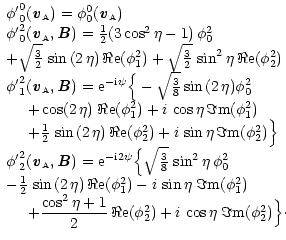 |
(17) |
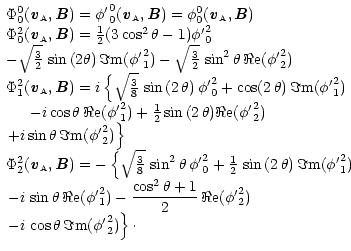 |
(18) |
Copyright ESO 2002