The Stokes parameters of the re-emitted radiation by moving atom with a velocity field
![]() are given as a function of the density matrix elements of the reemitted photons written in the frame of the line of sight (in number of reemitted photons per unit of time, per unit of volume and per unit of velocity distribution)
by the following relations (Sahal-Bréchot et al. 1998, 1986)
are given as a function of the density matrix elements of the reemitted photons written in the frame of the line of sight (in number of reemitted photons per unit of time, per unit of volume and per unit of velocity distribution)
by the following relations (Sahal-Bréchot et al. 1998, 1986)
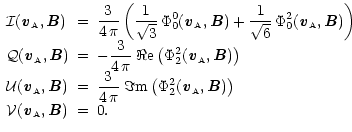 |
(19) |
The general form of the reemitted radiation Stokes parameters (here we take into account only of the linear polarization) is given by
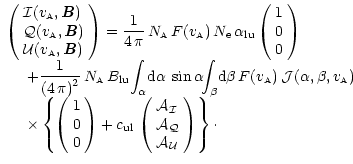 |
(20) |
From the forms of the equations giving the Stokes parameters as a function of the magnetic field and the velocity field, it is clear that the Hanle effect and the Doppler redistribution effect are completely decoupled. Particularly, by cancelling the magnetic field in the terms
![]() ,
,
![]() and
and
![]() ,
we obtain the results of Sahal-Bréchot et al. (1998) which give only the velocity-field effect. To obtain the Stokes parameters as a function of the magnetic field alone, we can just cancel the velocity field vector in the dimming term.
,
we obtain the results of Sahal-Bréchot et al. (1998) which give only the velocity-field effect. To obtain the Stokes parameters as a function of the magnetic field alone, we can just cancel the velocity field vector in the dimming term.
We note that we have assumed only the two-level atom approximation and there is no approximation on the incident and the reemitted line profiles. There is also no approximation on the velocity distribution
![]() of the scattering atoms. It can be isotropic as in the inner corona (although this point is not really clear) or anisotropic as observed by UVCS/SoHO in the high solar corona.
of the scattering atoms. It can be isotropic as in the inner corona (although this point is not really clear) or anisotropic as observed by UVCS/SoHO in the high solar corona.
Following Sahal-Bréchot et al. (1998), to get the distribution in frequency and intensity of the polarization of the scattered radiation, it is necessary to sum the contribution of all the
atoms having the velocity
![]() along
the line of sight. This can be performed by an integration
over the velocity field distributions
along
the line of sight. This can be performed by an integration
over the velocity field distributions
![]() and
and
![]() in the plane perpendicular to the line of sight.
in the plane perpendicular to the line of sight.
The Stokes parameters as a function of the scattered radiation frequency ![]() are given (in number of photons per unit of time, per unit of volume, per unit of frequency and per unit of solid angle) by
are given (in number of photons per unit of time, per unit of volume, per unit of frequency and per unit of solid angle) by
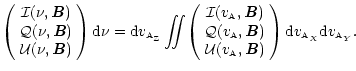 |
(21) |
Copyright ESO 2002