A spatially isolated, spherical N-body system is studied. The N particles of the system are accelerated by gravity, and forces induced by boundary conditions and perturbations, respectively. In all, a particle can be accelerated by five force types: 1) confinement 2) energy dissipation due to velocity dependent friction 3) external forcing 4) long-range attraction (self-gravity) and 5) short-range repulsion. The five force types are discussed in detail in Sects. 3.2-3.5.
A steep potential well confines the particles to a sphere of radius
![]() (see Sect. 3.2). The total mass M and the
gravitational constant G equal one as well, G=M=1. The
dimensionless energy is the energy measured in units of GM2/R, that
is in our model
(see Sect. 3.2). The total mass M and the
gravitational constant G equal one as well, G=M=1. The
dimensionless energy is the energy measured in units of GM2/R, that
is in our model ![]() .
Thus energies and other quantities with
energy dimension (like the temperature) can be considered as
dimensionless.
.
Thus energies and other quantities with
energy dimension (like the temperature) can be considered as
dimensionless.
The confinement is realized through a steep potential well
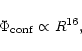 |
(2) |
Unlike non-spherical reflecting enclosures, the applied potential well conserves angular momentum.
The effect of different dissipation schemes is studied: local dissipation, global dissipation and a scheme similar to dynamical friction. For convenience we call the latter hereafter "dynamical friction''.
The local dissipation scheme represents inelastic scattering of interstellar gas constituents. That is, friction forces are added that depend on the relative velocities and positions of the neighboring particles.
A particle is considered as a neighbor if its distance is
![]() ,
where
,
where ![]() is the softening length and
is the softening length and
![]() is a free parameter. The friction force has the form:
is a free parameter. The friction force has the form:
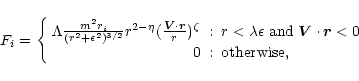 |
(3) |
For
![]() the friction force is
the friction force is
The global dissipation depends not on the relative velocity V, but on
the absolute particle velocity v. The global friction force is
| (5) |
Setting the velocity-dispersion
![]() ,
which is the dispersion of a virialized
self-gravitating system with M=R=1,
Chandrasekhar's dynamical friction formula
can be parameterized to a good approximation by,
,
which is the dispersion of a virialized
self-gravitating system with M=R=1,
Chandrasekhar's dynamical friction formula
can be parameterized to a good approximation by,
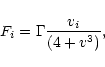 |
(6) |
If the dissipated energy is replenished by a forcing scheme the system
can be subjected to a continuous energy-flow. Here the energy
injection is due to time-dependent boundary conditions, that is, due
to a perturbation potential. This perturbation should on the one hand
be non-periodic and quasi-stochastic, on the other hand it should
provide an approximately regular large-scale energy injection in
time-average. A simple perturbation potential, meeting these
conditions, has the linear form,
![\begin{displaymath}\Phi_{\rm pert}(x,y,z,t)=\gamma [B_x(t) x + B_y(t) y + B_z(t) z],
\end{displaymath}](/articles/aa/full/2002/16/aa1730/img82.gif) |
(7) |
The perturbations are a linear combination of stationary waves that do not inject momentum.
If our system represents a molecular cloud then a perturbation similar
to those described above can be due to star clusters, clouds or other
massive objects passing irregularly in the vicinity. Indeed such
stochastic encounters must be quite frequent in galactic disks and we
assume that the average time between two encounters is,
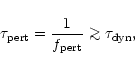 |
(9) |
Such a low frequency forcing scheme induces at first ordered particle motions, which are transformed in the course of time to random thermal motion, due to gravitational particle interaction.
Interaction forces include self-gravity and repulsive
forces whose strength can be adjusted by a parameter.
Repulsive forces may be a result of sub-resolution
processes such as star-formation or quantum degeneracy.
The particle interaction potential reads,
![\begin{figure}
\par\par\includegraphics[angle=90,width=7.4cm,clip]{1730f1.eps}
\end{figure}](/articles/aa/full/2002/16/aa1730/Timg102.gif) |
Figure 1:
The potential as a function of r in units of
Gm/R, where m is the particle mass. A test
particle at
|
The interaction forces are computed on the Gravitor Beowulf
Cluster![]() at the Geneva Observatory with a parallel
tree code. This code is based on the Fortran
Barnes & Hut (1986, 1989) tree algorithm,
and has been efficiently parallelized for
a Beowulf cluster. It is available on request.
at the Geneva Observatory with a parallel
tree code. This code is based on the Fortran
Barnes & Hut (1986, 1989) tree algorithm,
and has been efficiently parallelized for
a Beowulf cluster. It is available on request.
The time-integration is the leap-frog algorithm with uniform
time-step, which ensures the conservation of the symplectic structure
of the conservative dynamics. The time-step is,
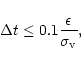 |
(11) |
The accuracy of the force computation is given through the tolerance
parameter, which for the studies presented in this paper is
![]() .
.
In order to test the code, the evolution of the
angular momentum is checked. We find that the angular momentum Jof a system with ![]() particles and local dissipation scheme,
that is initially
particles and local dissipation scheme,
that is initially
![]() in units such that
energy is dimensionless, remains small,
in units such that
energy is dimensionless, remains small,
![]() .
This is illustrated by means of two examples. Two simulations with
equal dissipation strength are carried out. One with short range
repulsion,
.
This is illustrated by means of two examples. Two simulations with
equal dissipation strength are carried out. One with short range
repulsion, ![]() ,
and the other without,
,
and the other without, ![]() .
After 10crossing times the angular momentum is
.
After 10crossing times the angular momentum is
![]() and
and
![]() ,
respectively. The deviation from the initial
value is larger for the simulation without short-range repulsion.
This is because the dissipation leads in this case to a
stronger mass concentration, i.e., to shorter particle distances.
Indeed, the potential energy after 10 crossing times is
,
respectively. The deviation from the initial
value is larger for the simulation without short-range repulsion.
This is because the dissipation leads in this case to a
stronger mass concentration, i.e., to shorter particle distances.
Indeed, the potential energy after 10 crossing times is
![]() and
and
![]() for the simulation with and without short-range
repulsion, respectively.
for the simulation with and without short-range
repulsion, respectively.
The different dissipation schemes, the forcing scheme and the
interaction potential with the short-distance repulsive force, have
several free parameters. In order to do a reasonably sized parameter
study the particle number has to be limited to a maximum of
![]() .
However, the absolute particle number is not important,
but the effect of changing it is. Thus, N also is varied.
.
However, the absolute particle number is not important,
but the effect of changing it is. Thus, N also is varied.
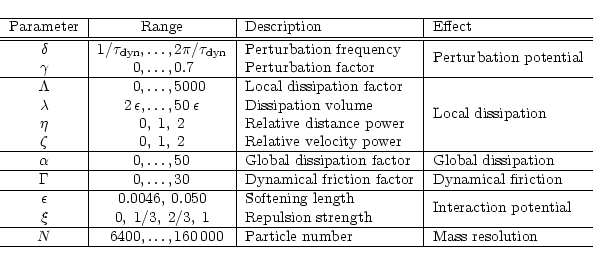
The model parameters and their ranges are indicated in Table 1.
|
|
Copyright ESO 2002