2 Gravo-thermal statistics

By confining a gravitational system within a sphere, we can compare our numerical work with previous analytical studies using the tools of statistical mechanics and point out some discrepancies. Although the theory, sometimes referred to as gravo-thermal statistics, is not fully consistent, since the applied Gibbs-Boltzmann entropy is derived under the assumption of extensivity (this inconsistency was recalled, e.g., by Taruya & Sakagami 2001), it yields some important and instructive results.

Before we present the model and the results let us here briefly review some theoretical findings (see Padmanabhan 1990 for an extended discussion on the topic).

Antonov (1962) and Lynden-Bell & Wood (1968) studied theoretically the thermodynamics of self-gravitating isothermal spheres and found anomalous behavior when compared with classical thermodynamics of extensive systems. An example of such an anomalous behavior is the so-called gravo-thermal catastrophe that occurs when an isothermal gas of energy E(<0) and mass M is released within a spherical box of radius greater than Antonov's radius, $r_{\rm A}=0.335 G M^2/(-E)$. The analytical model predicts that for such systems there is no equilibrium to go and nothing can stop the collapse of the central parts.

Antonov's and Lynden-Bell & Wood's investigations have based on point-like particles. Since then, several studies have been carried out with modified (i.e., non point-like) particle potentials. Hertel & Thirring (1971) modified the gravitational interaction potential by introducing short-distance repulsive forces due to quantum degeneracy and Aronson & Hansen (1972) investigated the behavior of self-gravitating hard-spheres (see also Chavanis & Sommeria 1998). Finally, Follana & Laliena (2000) applied softened interaction potentials. They all found qualitatively the same result: Unlike the model of Lynden-Bell & Wood, there is always an equilibrium state for finite size particles. However, a phase transition, separating a high energy homogeneous phase from a low energy collapsing phase with core-halo structure, occurs in an energy interval with negative microcanonical specific heat,

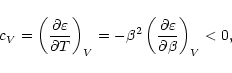$$c_V= \left(\frac{\partial\varepsilon}{\partial T}\right)_V= -... ...a^2\left(\frac{\partial\varepsilon}{\partial\beta}\right)_V<0,$$ (1)

where $\varepsilon$ is the total energy and $\beta=1/T$ is the inverse temperature.

There are fewer theoretical works done with the grand canonical ensemble (e.g. de Vega et al. 1996) where mass would be allowed to be exchanged with the environment, therefore we limit the scope of this study to the canonical ensemble, that is, energy can be exchanged with the environment, but not the mass and angular momentum.

Note that an ensemble allowing also the exchange of angular momentum would be very relevant for astrophysical situations, but few theoretical works have been made on this important aspect (Laliena 1999; Fliegans & Gross 2001).