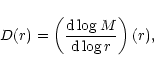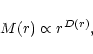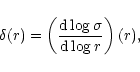Up: Long-range correlations in self-gravitating
In order to check if the perturbations of the gravitational system
induce characteristic correlations in phase-space, the indices
D and 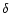 of the mass-size
relation and the velocity-dispersion-size relation
are determined.
of the mass-size
relation and the velocity-dispersion-size relation
are determined.
The index of the mass-size relation can be found via,
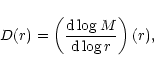 |
(12) |
where M is the sum of the masses of all particles having
a relative distance r. The mass size relation is then
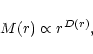 |
(13) |
where r can be considered as the scale. For a homogeneous mass
distribution and for a hierarchical fragmented, fractal structure the
index is a constant. For the latter case the index is not necessarily
an integer and lies in the interval,
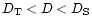 ,
where
,
where
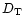 and
and 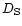 are the topological dimension and the
dimension of the embedding space, respectively (Mandelbrot
1982).
are the topological dimension and the
dimension of the embedding space, respectively (Mandelbrot
1982).
The index of the velocity-dispersion-size relation is
determined by,
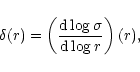 |
(14) |
where 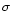 is the velocity-dispersion of
all particles having a relative distance r.
Observations of the interstellar medium
suggest a constant index
is the velocity-dispersion of
all particles having a relative distance r.
Observations of the interstellar medium
suggest a constant index
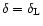 on
scales
on
scales
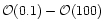 pc with
pc with
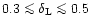 .
This is expressed by
Larson's law (e.g. Larson 1981; Scalo 1985;
Falgarone & Perault 1987; Myers & Goodman 1988)
.
This is expressed by
Larson's law (e.g. Larson 1981; Scalo 1985;
Falgarone & Perault 1987; Myers & Goodman 1988)
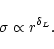 |
(15) |
In order to preclude the effect of boundary conditions
on the scaling relations,
upper and lower cutoffs have to be taken into account.
The lower cutoff is given by the softening length.
An upper cutoff arises from the final system size.
Thus, the scope of application is for the
velocity-dispersion-size and the mass-size
relation,
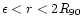 ,
and
,
and
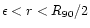 ,
respectively, where
R90 is the radius of the sphere centered at the
origin which contains
,
respectively, where
R90 is the radius of the sphere centered at the
origin which contains 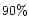 of the mass
(see Huber & Pfenniger 2001a).
of the mass
(see Huber & Pfenniger 2001a).


Up: Long-range correlations in self-gravitating
Copyright ESO 2002
![]() of the mass-size
relation and the velocity-dispersion-size relation
are determined.
of the mass-size
relation and the velocity-dispersion-size relation
are determined.