Here, some N-body gravo-thermal experiments of systems with weak dissipation, i.e., of systems in quasi-equilibrium are presented. The results are compared with theoretical findings.
In order to cover a range of energy with the same experiment, we
introduce a weak global dissipation scheme allowing us to describe a
range of quasi-equilibrium states. Here weak means that
![]() ,
where
,
where
![]() is the dissipation
time-scale. Then, the results can be compared with theoretical
equilibrium states.
is the dissipation
time-scale. Then, the results can be compared with theoretical
equilibrium states.
Follana & Laliena (2000) theoretically examined the
thermodynamics of self-gravitating systems with softened potentials.
They soften the Newtonian potential by keeping n terms of an
expansion in spherical Bessel functions (hereafter such a regularized
potential is called a Follana potential). This regularization allows
the calculation of the thermodynamical quantities of a
self-gravitating system. The form of their potential is similar to a
Plummer potential with a corresponding softening
length. Figure 2 shows a softened Follana
potential with n=10, and a Plummer potential with
![]() .
.
![\begin{figure}
\par\includegraphics[angle=90,width=7.4cm,clip]{1730f2.eps}
\end{figure}](/articles/aa/full/2002/16/aa1730/Timg128.gif) |
Figure 2:
The Follana (n=10) and the Plummer
(
|
In their theoretical work Follana & Laliena found for a mild enough
regularization (n<30) a phase transition below the critical energy
![]() in a region with negative specific
heat. The transition separates a high energy homogeneous phase from a
low energy collapsed phase with a core-halo structure.
in a region with negative specific
heat. The transition separates a high energy homogeneous phase from a
low energy collapsed phase with a core-halo structure.
We want to reproduce these findings by applying
a Plummer potential (![]() ). Furthermore,
the effect of a small-scale repulsive force
(
). Furthermore,
the effect of a small-scale repulsive force
(![]() )
is studied.
)
is studied.
For these purposes, simulations with a weak global dissipation
strength,
![]() ,
are carried out. The dissipation time is
then
,
are carried out. The dissipation time is
then
![]() ,
where the free fall time is
,
where the free fall time is
![]() .
.
Before we discuss the results, let us briefly present some model
properties. The initial state is a relaxed, unperturbed and confined
N-body sphere with total energy
![]() .
.
Assigning a particle a volume of
![]() ,
the
volume filling factor is,
,
the
volume filling factor is,
The applied weak dissipation strength maintains the system
approximately thermalized and virialized (see Fig. 3).
Here a system of N particles is called virialized when the moment of
inertia I is not accelerated,
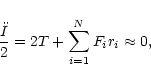 |
(17) |
The evolution of the inverse temperature
![]() as a function of the total energy
as a function of the total energy
![]() for two
simulations with
for two
simulations with ![]() and
and ![]() ,
respectively, as well as the
semi-analytical curve calculated by Follana & Laliena are shown in
the left panel of Fig. 4.
,
respectively, as well as the
semi-analytical curve calculated by Follana & Laliena are shown in
the left panel of Fig. 4.
For the simulation with the Plummer potential the interval of negative
specific heat agrees with theoretical predictions. Also, in
accordance with predictions, a phase transition takes place,
separating a high energy homogeneous phase from a collapsed phase in
a interval with negative specific heat. Yet, the simulated phase
transitions occur at higher energies. To illustrate this the
evolution of the Lagrangian radii ![]() are shown in the middle
and the right panel of Fig. 4.
are shown in the middle
and the right panel of Fig. 4.
In the high energy homogeneous phase the system is insensitive to the short-distance form of the potential. Thus all systems enter the interval of negative specific heat at the same energy. However, the collapsed phase is sensitive to the short-distance form. That is, the system with repulsive short-distance force re-enters the interval of positive specific heat at a higher energy than those without such forces (see left panel of Fig. 4).
Furthermore, the collapsed phase resulting from a simulation with a Plummer potential is hotter and denser than those resulting from a simulation with repulsive small scale forces. This can be seen in Fig. 4 as well.
For a smaller softening length, theory expects a phase transition at higher
energies. Yet, already in simulations with a mild softening
![]() the collapsing transition occurs straight after the
system has entered the interval of negative specific heat, which is
shortly after the system has become self-gravitating. Thus, the
collapsing transition cannot occur at significantly
higher energies for a smaller softening length.
the collapsing transition occurs straight after the
system has entered the interval of negative specific heat, which is
shortly after the system has become self-gravitating. Thus, the
collapsing transition cannot occur at significantly
higher energies for a smaller softening length.
However, for systems with smaller softening length, the energy at which the
system reenters the zone of positive specific heat after the collapse
changes, i.e., it is shifted to smaller energies. This is shown in
Fig. 5, where two simulations with
![]() and
and
![]() resp.
resp.
![]() are compared.
are compared.
![\begin{figure}
\par\includegraphics[angle=90,width=17.8cm,clip]{1730f5.eps}
\end{figure}](/articles/aa/full/2002/16/aa1730/Timg142.gif) |
Figure 5:
Same as Fig. 4 for two simulations with
|
Due to the higher particle number the dissipation time is in these
simulations reduced to
![]() .
Thus,
dynamical equilibrium is not as perfect as previously. That is,
the acceleration of the
moment of inertia I attains a maximum value of,
.
Thus,
dynamical equilibrium is not as perfect as previously. That is,
the acceleration of the
moment of inertia I attains a maximum value of,
![]() ,
where T is the kinetic energy. However, in general dynamical
equilibrium is well approximated and we expect, due to the experience
with simulations with varying particle number and dissipation time,
that the effect of the temporal deviation from equilibrium does not
affect qualitatively the results presented in Fig. 5.
,
where T is the kinetic energy. However, in general dynamical
equilibrium is well approximated and we expect, due to the experience
with simulations with varying particle number and dissipation time,
that the effect of the temporal deviation from equilibrium does not
affect qualitatively the results presented in Fig. 5.
The volume filling factor of the systems with
![]() and
and
![]() is
is
![]() ,
meaning that
the mass resolution is a factor 2.7 larger than the force resolution.
Thus the system is less granular than in the previous simulations with
N=8000 and
,
meaning that
the mass resolution is a factor 2.7 larger than the force resolution.
Thus the system is less granular than in the previous simulations with
N=8000 and
![]() (see Fig. 4). Yet, this
does not affect the simulated quasi-equilibrium states and the
deviation from theoretical predictions remains.
(see Fig. 4). Yet, this
does not affect the simulated quasi-equilibrium states and the
deviation from theoretical predictions remains.
Some predictions made by analytical models, such as the interval of
negative specific heat, agree with findings resulting from N-body
models. Yet, discrepancies also appear, such as the way the
collapsing phase transition develops.
At first glance the deviating results are surprising. Yet the small scale physics is different in the two models, which may account for the discrepancies. Indeed, thermostatistics assumes a smooth density distribution and is thus not able to account for two-body relaxation effects in granular media. However, a certain degree of granularity is an inherent property of N-body systems. This may then lead to discrepancies, especially in the unstable interval of negative specific heat, where phase transitions may be sensitive to small scale physics.
While thermostatistics is too smooth to account for microscopic physics in granular self-gravitating media such as the interstellar gas, two-body relaxation is often too strong in N-body systems due to computational limitations. This is particularly so in high force resolution simulations where the force resolution is larger than the mass resolution. We refer to this in Sect. 6.1 where we discuss, among other things, the effect of the granularity on long-range correlations appearing in the interval of negative specific heat.
A further discrepancy between nature, analytical models and N-body models may be due to the entropy used in gravo-thermal statistics (Taruya & Sakagami 2001). Indeed, the entropy used in analytical models to find equilibrium states via the maximum entropy principle is the extensive Boltzmann-Gibbs entropy, that is in fact not applicable for non-extensive self-gravitating systems.
Generalized thermostatistics including non-extensivity are currently developed (Tsallis 1988; Sumiyoshi 2001; Latora et al. 2001; Leubner 2001). These formalisms suggest that non-extensivity changes not all but some of the classical thermodynamical results (Tsallis 1999; Boghosian 1999), which agrees with our findings.
Because currently it is a priori not known which thermostatistical properties change in non-extensive systems and consistent theoretical tools are not available, analytical results must be considered with caution.
Copyright ESO 2002