

Up: The origin of the
Subsections
Let us consider a gas cloud (or blob) model in the form of a spherical region of
radius R, which contains FeII ions, which, all over the volume of the region,
are subject to homogeneous excitation within the limits of the Doppler profile and,
hence, emit spontaneously within the limits of the Doppler line width. The
optical thickness of the region, with reference to the line center of the
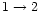 transition,
transition,
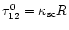 (notation in
Johansson & Letokhov 2001b), will vary over the range
(notation in
Johansson & Letokhov 2001b), will vary over the range
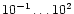 ,
where
,
where
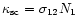 is the coefficient of resonance scattering per
unit length,
is the coefficient of resonance scattering per
unit length,
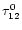 is the radiative transition cross section with
reference to the line center, and N1 is the concentration of the FeII
ions in the state 1. The coefficient of nonresonant (continuous) absorption
per unit length,
is the radiative transition cross section with
reference to the line center, and N1 is the concentration of the FeII
ions in the state 1. The coefficient of nonresonant (continuous) absorption
per unit length,
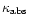 ,
will vary relative to
,
will vary relative to
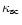 within
the limits of
within
the limits of
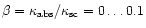 .
Thus, at high
.
Thus, at high
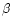 and
and
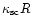 values (
values (
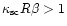 )
nonresonant
absorption per unit physical size is high, but where
)
nonresonant
absorption per unit physical size is high, but where
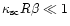 nonresonant absorption can be substantial only for a repeated
scattering of radiation, which increases the optical path length.
nonresonant absorption can be substantial only for a repeated
scattering of radiation, which increases the optical path length.
The equation for steady-state radiation intensity
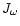 inside a
blob at the frequency
inside a
blob at the frequency 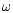 with a spherical scattering diagram
has the form (Sobolev 1949a)
with a spherical scattering diagram
has the form (Sobolev 1949a)
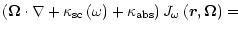 |
|
|
|
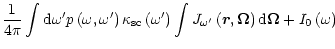 |
|
|
(26) |
where the spontaneous emission intensity of FeII at level 2 is described
by the term
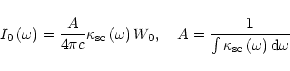 |
(27) |
and the normalization corresponds to the radiation density (in
photons/cm3). In this equation,
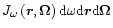 is the number of
photons contained in the volume d
is the number of
photons contained in the volume d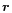 ,
having their frequencies in
the interval d
,
having their frequencies in
the interval d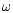 and moving within the limits of the solid angle
d
and moving within the limits of the solid angle
d
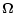 .
The factor
.
The factor
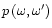 is the
probability that a photon of frequency
is the
probability that a photon of frequency 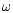 will be emitted after
the atom has interacted with a photon of frequency
will be emitted after
the atom has interacted with a photon of frequency
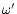 ,
,
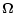 is the unit vector of the photon motion direction, and
is the unit vector of the photon motion direction, and
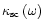 and
and
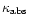 are the coefficients
of resonance scattering and nonresonant absorption per unit length at the
frequency
are the coefficients
of resonance scattering and nonresonant absorption per unit length at the
frequency 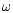 .
In the subsequent discussion we assume that the frequency
dependence of the scattering coefficient is due to the Maxwellian atomic velocity
distribution and has the form
.
In the subsequent discussion we assume that the frequency
dependence of the scattering coefficient is due to the Maxwellian atomic velocity
distribution and has the form
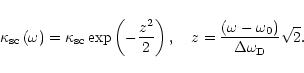 |
(28) |
Here we use the Doppler width definition, which is adopted in the astrophysical
literature (Mihalas 1978). This definition differs only by a factor of
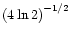 from the definition used in optical spectroscopy
(Svelto 1989).
from the definition used in optical spectroscopy
(Svelto 1989).
The transport Eq. (26) differs from the commonly used one in two
aspects. Firstly, intending to describe radiation in spherical blobs, we
consider a three-dimensional, spherically symmetric problem, whereas it is
usually a two-dimensional, plane problem that is subject to consideration.
Secondly, we assume that the frequency dependence of the radiation source,
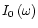 ,
is defined by the Doppler profile.
,
is defined by the Doppler profile.
Since the optical thickness we consider for the
 UV transition
in FeII is not very large (
UV transition
in FeII is not very large (
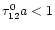 ), scattering takes place
inside the Doppler core (Mihalas 1978). In that case, photon scattering is completely
noncoherent, i.e., the scattering probability
), scattering takes place
inside the Doppler core (Mihalas 1978). In that case, photon scattering is completely
noncoherent, i.e., the scattering probability
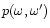 has the following form:
has the following form:
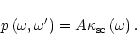 |
(29) |
In this approximation, Eq. (7) adopts the form
 |
|
|
|
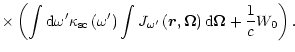 |
|
|
(30) |
Equation (30) describes the transfer of UV radiation inside the blob. To fully
formulate the problem, it is necessary to specify the boundary conditions at
the edge of the blob, which assumes no incoming flux into the blob.
However, it seems to be more convenient to formulate the problem in another
way, where we assume that radiation propagates in an infinite space, but scattering
occurs only at r<R. One can easily see that also in this case there is no
incoming flux on the surface of the blob, and by virtue of that
fact, the solutions of the different approaches to the same problem coincide
inside the blob. Thus, we have to solve the equation
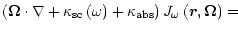 |
|
|
|
![$\displaystyle \left\{
\begin{array}[c]{c}%
\frac{A}{4\pi}\kappa_{\rm {sc}}\left...
...mega}+\frac{1}{c}W_{0}\right)
,r<R\\
0,\quad\quad\quad r>R.
\end{array}\right.$](/articles/aa/full/2002/13/aah3002/img197.gif) |
|
|
(31) |
If we do not consider the distribution of photons over the propagation
directions, we then can exclude from Eq. (31) the dependence on the
variable
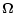 .
This can be achieved by taking the Fourier
transform in terms of spatial coordinates and then averaging over propagation
directions. As a result, we obtain the following integral equation for the
spectral density of photons in space,
.
This can be achieved by taking the Fourier
transform in terms of spatial coordinates and then averaging over propagation
directions. As a result, we obtain the following integral equation for the
spectral density of photons in space,
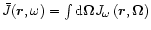 :
:
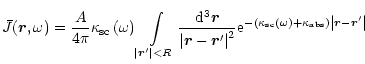 |
|
|
|
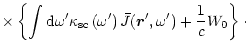 |
|
|
(32) |
As already noted, this equation correctly describes the true photon density
inside the blob only. In the case of spherical symmetry of the problem,
Eq. (32) may be reduced to the form (Sobolev 1949b):
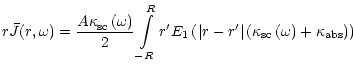 |
|
|
|
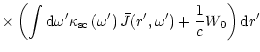 |
|
|
(33) |
where E1 is the integral exponential function (Abramovitz 1964).
For the total photon density in space,
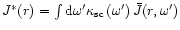 ,
we have from Eq. (33)
,
we have from Eq. (33)
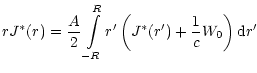 |
|
|
|
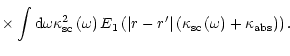 |
|
|
(34) |
Introducing the effective photon density (resonance-line source function)
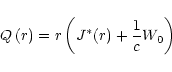 |
(35) |
we may represent the final integral equation in the form
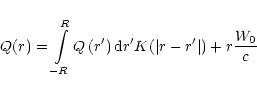 |
(36) |
where
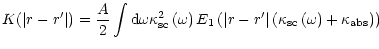 |
|
|
(37) |
and
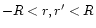 .
.
Given the solution of Eq. (37), we can find the spectral photon density
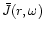 and the total photon density P(r) at any point inside
the blob:
and the total photon density P(r) at any point inside
the blob:
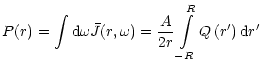 |
|
|
|
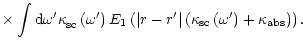 |
|
|
(39) |
At the edge of the blob
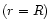 we have
we have
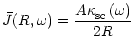 |
|
|
|
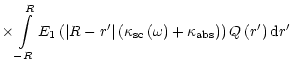 |
|
|
(42) |
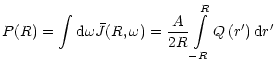 |
|
|
|
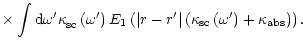 |
|
|
(41) |
The integral equation (Eq. (26)) can be solved either numerically or by the approximate
analytical methods (Sobolev 1949a; Ivanov 1973). In this work, we solve this
integral equation numerically, as we are interested in the radiation
characteristics at a wide variety of values of the scattering, absorption, etc. parameters, and analytical solutions are usually applicable only within limited
parameter regions. The dimensionless form of Eq. (36) is as follows:
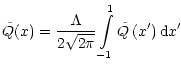 |
|
|
|
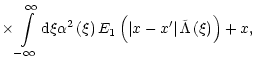 |
|
|
(42) |
where
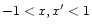 .
When obtaining Eqs. (36) to (42), we have introduced the following notations:
.
When obtaining Eqs. (36) to (42), we have introduced the following notations:
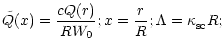 |
|
|
|
![$\displaystyle \tilde{\Lambda}\left( \xi\right) =\Lambda\left[ \alpha\left(
\xi\...
...eta\right] ,\alpha\left( \xi\right) =\exp\left( -\frac
{\xi^{2}}{2}\right)\cdot$](/articles/aa/full/2002/13/aah3002/img224.gif) |
|
|
(43) |
The integral transport Eq. (42) is often solved by approximating the kernel
with a set of exponents (Avrett & Hummer 1965). This approach, however, imposes
restrictions upon the form of the right-hand side of Eq. (26) and fails
to describe the singular character of the kernel adequately enough.
In the present work, we use the Galerkin method (Kalitkin 1978) and expand the
solution Q(x) of Eq. (42) into a trigonometric series:
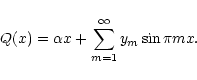 |
(44) |
The choice of expansion (28) is due to the odd character of Q(x) and the
fact that
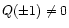 at the boundaries of the region. Substituting
expression (28) into (21), we get an infinite set of linear equations for
at the boundaries of the region. Substituting
expression (28) into (21), we get an infinite set of linear equations for
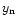 :
:
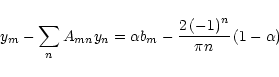 |
(45) |
where
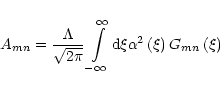 |
(46) |
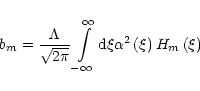 |
(47) |
and
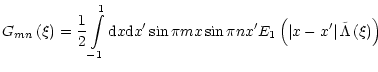 |
|
|
(48) |
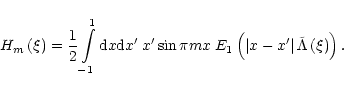 |
(49) |
The integrals Gmn and Hm can be expressed in terms of integral
exponential functions of complex variable:
Gmn=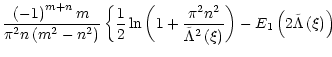 |
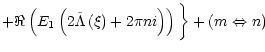 |
(50) |
The analytical calculation of integrals (50)-(52) in terms of coordinates
allows one to avoid the difficulties associated with the singular character of
the kernel. The integrals in terms of the dimensionless frequency 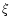 are
computed numerically. The infinite system (45) can be reduced to a
finite-dimensional one by simply eliminating the higher harmonics. In our
numerical computations, we included up to 700 harmonics. In doing so,
we determined the parameter
are
computed numerically. The infinite system (45) can be reduced to a
finite-dimensional one by simply eliminating the higher harmonics. In our
numerical computations, we included up to 700 harmonics. In doing so,
we determined the parameter  in this system so as to minimize
oscillations at the point x=0. The absence of oscillations corresponded to
the optimum choice of
in this system so as to minimize
oscillations at the point x=0. The absence of oscillations corresponded to
the optimum choice of
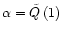 .
With the
parameter
.
With the
parameter  determined in this way, the Fourier series was summed by
the Fejer method (Courant & Hilbert 1962). As a result, we obtained a smooth solution of
Eq. (42). Figure 6 shows the solution of Eq. (42) at typical
parameter values (
determined in this way, the Fourier series was summed by
the Fejer method (Courant & Hilbert 1962). As a result, we obtained a smooth solution of
Eq. (42). Figure 6 shows the solution of Eq. (42) at typical
parameter values (
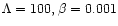 ).
).
![\begin{figure}
\par\includegraphics[width=8.8cm,clip]{Fig6.eps}\end{figure}](/articles/aa/full/2002/13/aah3002/Timg244.gif) |
Figure 6:
Source function Q(x) at
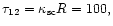 and
and
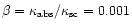 . . |
With integral Eq. (42) solved, the spectral radiation density and photon
density were found by direct numerical integration in accordance with
expressions (38)-(41).
To answer the question about the effect of continuous absorption on the
intensity of the spectral line observed, it is sufficient to calculate the
dependence of the spectrum-integrated radiation intensity at the boundary of
the spherical region on the parameters
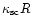 and
and
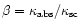 .
We will, however, present a much greater mass of
numerical data obtained, for they may also prove to be of interest in understanding
the origin and evolution of spectral lines inside the blob.
.
We will, however, present a much greater mass of
numerical data obtained, for they may also prove to be of interest in understanding
the origin and evolution of spectral lines inside the blob.
Figures 7 and 8 present the dependences of the spectral radiation density at
the center of the spherical blob on the transition frequency and optical
density
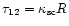 at various values of the nonresonance
absorption
at various values of the nonresonance
absorption
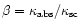 .
.
![\begin{figure}
\par\includegraphics[width=8.8cm,clip]{Fig7.eps}\end{figure}](/articles/aa/full/2002/13/aah3002/Timg248.gif) |
Figure 7:
Spectral radiation density at the center of the blob,
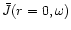 ,
as a function of the optical density in the absence of nonresonance absorption ,
as a function of the optical density in the absence of nonresonance absorption
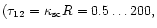
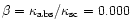 ),
normalized to the spectral density value at the center of the blob in the
absence of scattering. ),
normalized to the spectral density value at the center of the blob in the
absence of scattering. |
![\begin{figure}
\par\includegraphics[angle=-90,width=16cm,clip]{Fig8.eps}\end{figure}](/articles/aa/full/2002/13/aah3002/Timg250.gif) |
Figure 8:
Spectral radiation density at the center of nebulae,
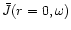 ,
as a function of the optical density ,
as a function of the optical density 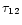
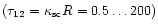 at various nonresonance absorption coefficients (
at various nonresonance absorption coefficients (
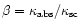 ), normalized to the spectral density value at the center of the
nebula in the absence of scattering: a) ), normalized to the spectral density value at the center of the
nebula in the absence of scattering: a)
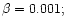 b)
b)
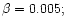 c) c)
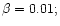 d)
d) 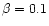 . . |
It can be seen from these
figures that when absorption is absent (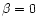 )
(Fig. 7), the line both
broadens monotonically and increases in intensity as the optical density grows
higher. When absorption is nonzero (Fig. 8), the line broadens with increasing
optical density, but its intensity reaches a maximum and then decreases. As
absorption grows higher (Fig. 8), the line intensity already starts
diminishing at low optical density values. Such a behavior of both the
broadening of the line and the reduction of its intensity with increasing
absorption is quite understandable: the line broadening is associated with
non-coherent scattering in each scattering event, whereas the reduction of the
line intensity at the center of the blob is due to the fact that the photons,
which formerly came to the center of the blob from its intermediate layers, can
no longer reach the center because of absorption.
)
(Fig. 7), the line both
broadens monotonically and increases in intensity as the optical density grows
higher. When absorption is nonzero (Fig. 8), the line broadens with increasing
optical density, but its intensity reaches a maximum and then decreases. As
absorption grows higher (Fig. 8), the line intensity already starts
diminishing at low optical density values. Such a behavior of both the
broadening of the line and the reduction of its intensity with increasing
absorption is quite understandable: the line broadening is associated with
non-coherent scattering in each scattering event, whereas the reduction of the
line intensity at the center of the blob is due to the fact that the photons,
which formerly came to the center of the blob from its intermediate layers, can
no longer reach the center because of absorption.
Figures 9 and 10 present the dependences of the spectral radiation density at
the edge of the blob on the frequency 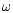 and optical density
and optical density 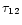 at various nonresonance absorption cross section values.
It can be seen from
these figures that at low absorption values and sufficiently high
at various nonresonance absorption cross section values.
It can be seen from
these figures that at low absorption values and sufficiently high 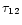 values there is the formation of the well-known doublet line structure (Figs. 9, 10a),
which
vanishes as absorption grows higher (Figs. 10b, c, and d). This is explained
quite naturally: only those photons can reach the boundary of the blob which
come from inside the thin layer next to its surface, wherein the number of
scattering events is small and so is, accordingly, the spectral diffusion effect.
values there is the formation of the well-known doublet line structure (Figs. 9, 10a),
which
vanishes as absorption grows higher (Figs. 10b, c, and d). This is explained
quite naturally: only those photons can reach the boundary of the blob which
come from inside the thin layer next to its surface, wherein the number of
scattering events is small and so is, accordingly, the spectral diffusion effect.
Figure 11 illustrates the dependence of the total photon density (normalized to
the photon density in the absence of scattering) at the center of the blob on
the scattering cross section and blob radius at various absorption
coefficients.
It can be seen that even here, as in the case of spectral
radiation density, the photon density in the absence of absorption increases
in a monotonic fashion as a result of the diffusive confinement effect. At
nonzero absorption values the photon density first grows slightly higher and
then decreases substantially.
A similar situation is also obtained for the photon density on the surface of the
blob, which governs the line intensity observed (Fig. 12).
In this case,
however, even in the absence of absorption, the photon density slowly tends to
1, i.e., the photon density on the surface of the major blob in the absence
of scattering, following a slight increase. The most important feature of Fig.
12 is the fact that the photon density rapidly drops with increasing
absorption coefficient as a result of the optical path length growing longer
in the absorbing medium.


Up: The origin of the
Copyright ESO 2002
![]() transition,
transition,
![]() (notation in
Johansson & Letokhov 2001b), will vary over the range
(notation in
Johansson & Letokhov 2001b), will vary over the range
![]() ,
where
,
where
![]() is the coefficient of resonance scattering per
unit length,
is the coefficient of resonance scattering per
unit length,
![]() is the radiative transition cross section with
reference to the line center, and N1 is the concentration of the FeII
ions in the state 1. The coefficient of nonresonant (continuous) absorption
per unit length,
is the radiative transition cross section with
reference to the line center, and N1 is the concentration of the FeII
ions in the state 1. The coefficient of nonresonant (continuous) absorption
per unit length,
![]() ,
will vary relative to
,
will vary relative to
![]() within
the limits of
within
the limits of
![]() .
Thus, at high
.
Thus, at high
![]() and
and
![]() values (
values (
![]() )
nonresonant
absorption per unit physical size is high, but where
)
nonresonant
absorption per unit physical size is high, but where
![]() nonresonant absorption can be substantial only for a repeated
scattering of radiation, which increases the optical path length.
nonresonant absorption can be substantial only for a repeated
scattering of radiation, which increases the optical path length.
![]() inside a
blob at the frequency
inside a
blob at the frequency ![]() with a spherical scattering diagram
has the form (Sobolev 1949a)
with a spherical scattering diagram
has the form (Sobolev 1949a)
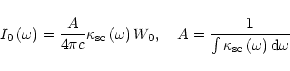
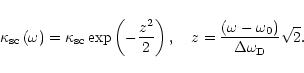
![]() ,
is defined by the Doppler profile.
,
is defined by the Doppler profile.
![]() UV transition
in FeII is not very large (
UV transition
in FeII is not very large (
![]() ), scattering takes place
inside the Doppler core (Mihalas 1978). In that case, photon scattering is completely
noncoherent, i.e., the scattering probability
), scattering takes place
inside the Doppler core (Mihalas 1978). In that case, photon scattering is completely
noncoherent, i.e., the scattering probability
![]() has the following form:
has the following form:
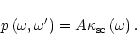
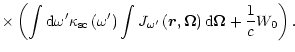
![$\displaystyle \left\{
\begin{array}[c]{c}%
\frac{A}{4\pi}\kappa_{\rm {sc}}\left...
...mega}+\frac{1}{c}W_{0}\right)
,r<R\\
0,\quad\quad\quad r>R.
\end{array}\right.$](/articles/aa/full/2002/13/aah3002/img197.gif)
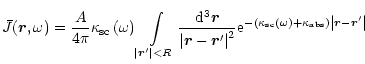
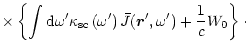
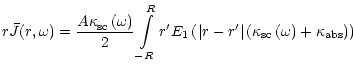
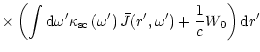
![]() ,
we have from Eq. (33)
,
we have from Eq. (33)
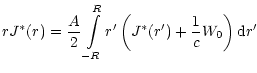
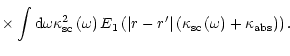
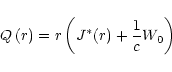
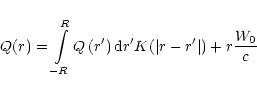
![]() and the total photon density P(r) at any point inside
the blob:
and the total photon density P(r) at any point inside
the blob:
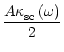
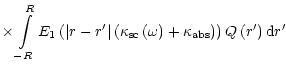
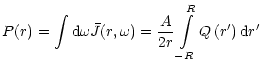
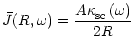
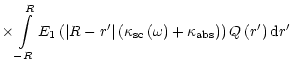
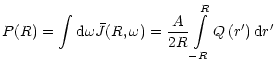
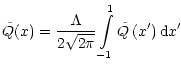
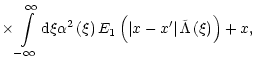
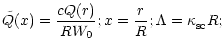
![$\displaystyle \tilde{\Lambda}\left( \xi\right) =\Lambda\left[ \alpha\left(
\xi\...
...eta\right] ,\alpha\left( \xi\right) =\exp\left( -\frac
{\xi^{2}}{2}\right)\cdot$](/articles/aa/full/2002/13/aah3002/img224.gif)
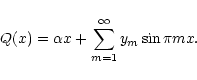
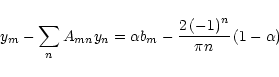
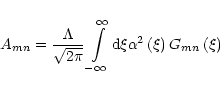
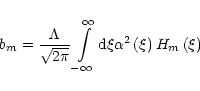
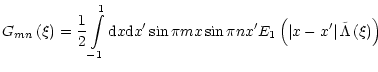
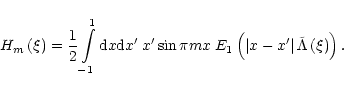
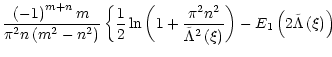
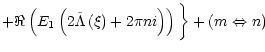
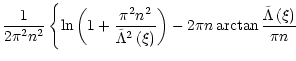
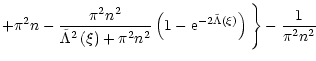
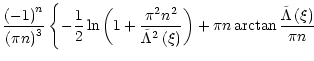
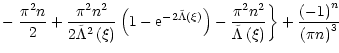
![]() and
and
![]() .
We will, however, present a much greater mass of
numerical data obtained, for they may also prove to be of interest in understanding
the origin and evolution of spectral lines inside the blob.
.
We will, however, present a much greater mass of
numerical data obtained, for they may also prove to be of interest in understanding
the origin and evolution of spectral lines inside the blob.
![]() at various values of the nonresonance
absorption
at various values of the nonresonance
absorption
![]() .
.
![]() and optical density
and optical density ![]() at various nonresonance absorption cross section values.
It can be seen from
these figures that at low absorption values and sufficiently high
at various nonresonance absorption cross section values.
It can be seen from
these figures that at low absorption values and sufficiently high ![]() values there is the formation of the well-known doublet line structure (Figs. 9, 10a),
which
vanishes as absorption grows higher (Figs. 10b, c, and d). This is explained
quite naturally: only those photons can reach the boundary of the blob which
come from inside the thin layer next to its surface, wherein the number of
scattering events is small and so is, accordingly, the spectral diffusion effect.
values there is the formation of the well-known doublet line structure (Figs. 9, 10a),
which
vanishes as absorption grows higher (Figs. 10b, c, and d). This is explained
quite naturally: only those photons can reach the boundary of the blob which
come from inside the thin layer next to its surface, wherein the number of
scattering events is small and so is, accordingly, the spectral diffusion effect.