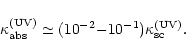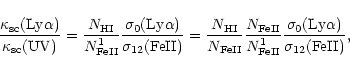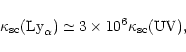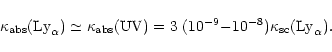Up: The origin of the
From the qualitative standpoint, the main result of this computer consideration
of Eqs. (43), (46), and (47), which are presented in Fig. 12, is as
follows: the change of the attenuation coefficients of two lines is inversely
proportional to the resonance scattering coefficients (see the asymptotes for
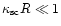 in Fig. 12). This asymptotic behaviour can be
approximated by the simple expression giving the intensity ratio between
the blob lines A and b on the surface of the blob:
in Fig. 12). This asymptotic behaviour can be
approximated by the simple expression giving the intensity ratio between
the blob lines A and b on the surface of the blob:
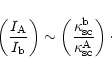 |
(53) |
Using a more detailed notation for the anomalous spectral lines and the
corresponding quantum transitions and energy levels (Fig. 13), one can
estimate the ratio between the resonance scattering coefficients:
Using the asymptotic ratio (53), we can obtain the following
expression for the blob and laboratory line intensity ratios:
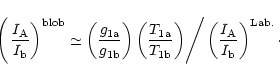 |
(55) |
A similar expression can also be obtained for the (C,d) pair of UV FeII lines:
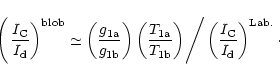 |
(56) |
The model considered above for the difference in attenuation between spectral
lines in resonance-scattering and nonresonance-absorbing media requires that
the difference between the lifetimes
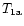 and
and
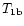 of the low-lying
levels (1a) and (1b) (or
of the low-lying
levels (1a) and (1b) (or
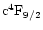 and
and
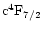 according to the
present identification of FeII levels) should be substantial:
according to the
present identification of FeII levels) should be substantial:
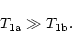 |
(57) |
![\begin{figure}
\par\includegraphics[width=8.8cm,clip]{Fig9NEW.ps}\end{figure}](/articles/aa/full/2002/13/aah3002/Timg263.gif) |
Figure 9:
Spectral radiation
density at the edge of the nebula,
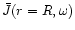 , as a function of
the optical density
, as a function of
the optical density
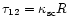 in the absence of
nonresonance absorption (
in the absence of
nonresonance absorption (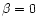 ), normalized to the spectral density value
at the edge of the nebula in the absence of scattering. ), normalized to the spectral density value
at the edge of the nebula in the absence of scattering. |
![\begin{figure}
\par\includegraphics[angle=-90,width=16cm,clip]{Fig10.eps}\end{figure}](/articles/aa/full/2002/13/aah3002/Timg265.gif) |
Figure 10:
Spectral radiation
density at the edge of the nebula,
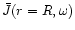 ,
as a function of the
optical density ,
as a function of the
optical density
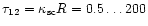 at various nonresonance
absorption cross sections, normalized to the spectral density value at the
center of the nebula in the absence of scattering: a)
at various nonresonance
absorption cross sections, normalized to the spectral density value at the
center of the nebula in the absence of scattering: a)
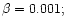 b)
b)
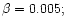 c)
c)
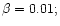 d)
d) 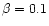 . . |
![\begin{figure}
\par\includegraphics[width=8.8cm,clip]{Fig11.eps}\end{figure}](/articles/aa/full/2002/13/aah3002/Timg266.gif) |
Figure 11:
Total photon
density at the center of the nebula as a function of the optical density
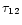 at various continuous absorption parameter values, normalized to
the total photon density value in the absence of scattering.
at various continuous absorption parameter values, normalized to
the total photon density value in the absence of scattering. |
![\begin{figure}
\par\includegraphics[width=8.8cm,clip]{Fig12.eps}\end{figure}](/articles/aa/full/2002/13/aah3002/Timg267.gif) |
Figure 12:
Total photon
density at the edge of the nebula as a function of the optical density
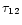 at various continuous absorption parameter values, normalized to
the total photon density value in the absence of scattering.
at various continuous absorption parameter values, normalized to
the total photon density value in the absence of scattering. |
![\begin{figure}
\par\includegraphics[width=8.8cm,clip]{fig13.eps}\end{figure}](/articles/aa/full/2002/13/aah3002/Timg268.gif) |
Figure 13:
Detailed notation
for the anomalous UV FeII spectral lines and the corresponding energy levels. |
It is only in this case that the weak (in lab.) lines are becoming more
strongly attenuated in the blob than their strong counterparts. This
requirement contradicts the existing data on the lifetimes of the lower
levels:
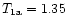 ms,
ms,
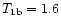 ms (Kurucz 1988).
ms (Kurucz 1988).
To fulfill the requirement, we should consider the possibility of the
photoionization depopulation of the lower levels by the Ly radiation (Johansson & Letokhov 2001b). The rate of this process is too low to provide
for any population inversion, but is quite sufficient to provide for the
depopulation of the lower levels at a rate much higher than the radiative
decay rate 1/T1. According to Johansson & Letokhov (2001b), for the effective
temperature of Ly
radiation (Johansson & Letokhov 2001b). The rate of this process is too low to provide
for any population inversion, but is quite sufficient to provide for the
depopulation of the lower levels at a rate much higher than the radiative
decay rate 1/T1. According to Johansson & Letokhov (2001b), for the effective
temperature of Ly
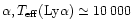 K, the
resonance enhancement of the photoionization cross-section can provide for the
depopulation of the lower states at a rate of
K, the
resonance enhancement of the photoionization cross-section can provide for the
depopulation of the lower states at a rate of
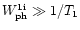 .
It is
most important that the narrow resonances of the photoionization
cross-sections of Fe II (Nahar & Pradhan 1994) and the energy difference between the
levels
.
It is
most important that the narrow resonances of the photoionization
cross-sections of Fe II (Nahar & Pradhan 1994) and the energy difference between the
levels
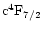 and
and
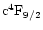 (Fig. 4,
(Fig. 4,
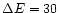 cm-1)
must provide for the preferable depopulation of the
cm-1)
must provide for the preferable depopulation of the
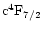 state (1b)
and the resulting weaker absorption of the A and C ultraviolet lines. According to (38),
it is necessary that the
state (1b)
and the resulting weaker absorption of the A and C ultraviolet lines. According to (38),
it is necessary that the
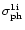 ratio should be
ratio should be
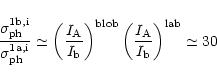 |
(58) |
which can be proved by precise calculations similar to those reported in
(Nahar & Pradhan 1994) in the range slightly above the ionization limit of FeII. The requirement
in Eq. (58) is rahter unusual for photoionization of levels belonging to the same LS term of an electron
configuration. Perhaps, this contradiction can be overcome in the frame of plausible photodepletion
of the c4F levels by relatively narrow autoionization levels (Johansson & Letokhov 2001b, Fig. 9).
However, this is subject to more detailed and elaborative atomic structure calculations and/or experiments, which are out of the scope of the present paper.
The estimates in Eq. (58) require the following value of
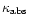 (UV):
(UV):
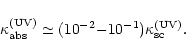 |
(59) |
This requirement must be compatible with the need for the Ly photons to be scattered many times,
photons to be scattered many times,
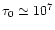 ,
prior to their
decay (Johansson & Letokhov 2001b) to provide for a substantial diffusive broadening of
the Ly
,
prior to their
decay (Johansson & Letokhov 2001b) to provide for a substantial diffusive broadening of
the Ly spectrum. The most suitable non-resonance absorption mechanism
is the photoionization absorption of He I to long-lived metastable states that are
known to accumulate in the passive HI region during the HeI/HeII/He*I
photoionization/recombination cycle under the effect of the shorter-wavelength
EUV radiation from the central star (Ambartzumian 1939). Let us assume
that the continuous absorption coefficients
spectrum. The most suitable non-resonance absorption mechanism
is the photoionization absorption of He I to long-lived metastable states that are
known to accumulate in the passive HI region during the HeI/HeII/He*I
photoionization/recombination cycle under the effect of the shorter-wavelength
EUV radiation from the central star (Ambartzumian 1939). Let us assume
that the continuous absorption coefficients
 are of the same order of magnitude for Ly
are of the same order of magnitude for Ly and UV
FeII photons, i.e.
and UV
FeII photons, i.e.
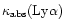 .
It follows from these crude
estimates that the ratio between the resonance scattering coefficients for
these two wavelengths is
.
It follows from these crude
estimates that the ratio between the resonance scattering coefficients for
these two wavelengths is
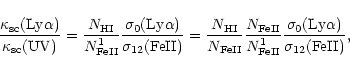 |
(60) |
where
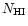 and
and
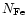 are the hydrogen and iron concentrations in the
blob, respectively. The factor
are the hydrogen and iron concentrations in the
blob, respectively. The factor
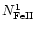 is the concentration of FeII ions in
the long-lived state 1 (c4F), which governs the optical density of the
is the concentration of FeII ions in
the long-lived state 1 (c4F), which governs the optical density of the
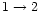 transition and the value is, according to the estimates presented in
Johansson & Letokhov (2001b),
transition and the value is, according to the estimates presented in
Johansson & Letokhov (2001b),
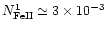
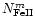 ,
where m
is the metastable state. If we
take the standard estimate for
,
where m
is the metastable state. If we
take the standard estimate for
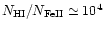 ,
we
get from relation (60)
,
we
get from relation (60)
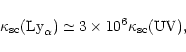 |
(61) |
and so requirement (59) corresponds to
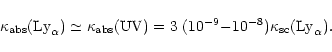 |
(62) |
Such a weak absorption of the Ly photons with their short
scattering length is known to provide for the necessary number of their
scattering events,
photons with their short
scattering length is known to provide for the necessary number of their
scattering events,
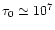 .
.


Up: The origin of the
Copyright ESO 2002
![]() in Fig. 12). This asymptotic behaviour can be
approximated by the simple expression giving the intensity ratio between
the blob lines A and b on the surface of the blob:
in Fig. 12). This asymptotic behaviour can be
approximated by the simple expression giving the intensity ratio between
the blob lines A and b on the surface of the blob:
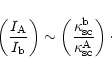
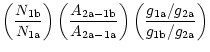
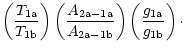
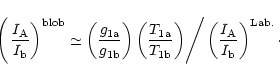
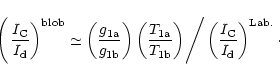
![\begin{figure}
\par\includegraphics[width=8.8cm,clip]{fig13.eps}\end{figure}](/articles/aa/full/2002/13/aah3002/Timg268.gif)
![]() radiation (Johansson & Letokhov 2001b). The rate of this process is too low to provide
for any population inversion, but is quite sufficient to provide for the
depopulation of the lower levels at a rate much higher than the radiative
decay rate 1/T1. According to Johansson & Letokhov (2001b), for the effective
temperature of Ly
radiation (Johansson & Letokhov 2001b). The rate of this process is too low to provide
for any population inversion, but is quite sufficient to provide for the
depopulation of the lower levels at a rate much higher than the radiative
decay rate 1/T1. According to Johansson & Letokhov (2001b), for the effective
temperature of Ly
![]() K, the
resonance enhancement of the photoionization cross-section can provide for the
depopulation of the lower states at a rate of
K, the
resonance enhancement of the photoionization cross-section can provide for the
depopulation of the lower states at a rate of
![]() .
It is
most important that the narrow resonances of the photoionization
cross-sections of Fe II (Nahar & Pradhan 1994) and the energy difference between the
levels
.
It is
most important that the narrow resonances of the photoionization
cross-sections of Fe II (Nahar & Pradhan 1994) and the energy difference between the
levels
![]() and
and
![]() (Fig. 4,
(Fig. 4,
![]() cm-1)
must provide for the preferable depopulation of the
cm-1)
must provide for the preferable depopulation of the
![]() state (1b)
and the resulting weaker absorption of the A and C ultraviolet lines. According to (38),
it is necessary that the
state (1b)
and the resulting weaker absorption of the A and C ultraviolet lines. According to (38),
it is necessary that the
![]() ratio should be
ratio should be
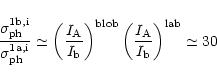
![]() (UV):
(UV):