An essential result of the discussion in (Johansson & Letokhov 2001b) is the possible evidence
for a (in the case of bright UV lines) significant optical density,
![]() ,
for UV transitions terminating on long-lived states. A
second important feature is the physical difference between the strong and
weak pairs of UV lines, namely, that they terminate on
different fine-structure levels (!), which we have denoted as levels 1.
Under laboratory conditions (optically thin, non-absorbing media), the intensity ratio
between, for example, transition A (2a
,
for UV transitions terminating on long-lived states. A
second important feature is the physical difference between the strong and
weak pairs of UV lines, namely, that they terminate on
different fine-structure levels (!), which we have denoted as levels 1.
Under laboratory conditions (optically thin, non-absorbing media), the intensity ratio
between, for example, transition A (2a
![]() 1b)
and transition b (2a
1b)
and transition b (2a
![]() 1a) is:
1a) is:
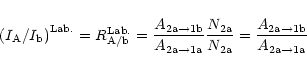 |
(20) |
Under blob conditions, we should take into account the possible
difference in optical pathway for photons associated with different
transitions as a result of a possible difference in the mean resonance
scattering lengths in optically thick media (
![]() ). The
resulting difference in attenuation,
). The
resulting difference in attenuation,
![]() ,
in the presence of
weak nonresonant (continuous) absorption
,
in the presence of
weak nonresonant (continuous) absorption
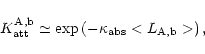 |
(21) |
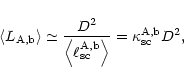 |
(22) |
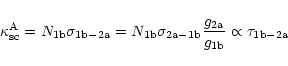 |
(23) |
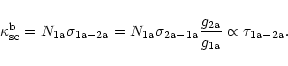 |
(24) |
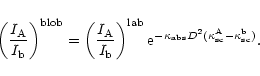 |
(25) |
The effect of nonresonant absorption of the flux of emission lines having different
optical path lengths in a
resonance-scattering medium of large optical thickness was considered long ago
(Hummer 1968). We have, in essence, rediscovered this effect when trying to
find an explanation for the anomalous behavior of the intensities of two pairs
of close spectral lines. The qualitative picture above does not take into
account the Doppler frequency shift caused by resonance scattering by
moving FeII ions. Actually the frequency-shifted photons can escape from the
blob at the depth
![]() .
This effect will limit the optical
pathways
.
This effect will limit the optical
pathways
![]() for trapped spectral lines
(Adams 1972; Harrington 1973; Hummer & Kunasz 1980). Hummer (1968) investigated
in detail the
special functions arising in radiative transfer due to nonresonance
scattering and the numerical
solution of the transport equation for the case of scattering with complete
frequency redistribution. Subject to consideration in Hummer's work (1968) was radiative
transfer in a plane-parallel layer with radiation sources both in a line spectrum
and in a continuous spectrum. In addition, the source of the line radiation in Hummer's work
contained some part due to the absorption of photons as a result of electron
collisions with the excited atom. The radiative transfer process in a medium
with non-resonant absorption in the case of partial frequency redistribution
was investigated both numerically and asymptotically in (Hummer & Kunasz 1980;
Frisch 1980),
where effective scaling laws were found for the case of small absorption
coefficients and large optical thicknesses of the layer.
for trapped spectral lines
(Adams 1972; Harrington 1973; Hummer & Kunasz 1980). Hummer (1968) investigated
in detail the
special functions arising in radiative transfer due to nonresonance
scattering and the numerical
solution of the transport equation for the case of scattering with complete
frequency redistribution. Subject to consideration in Hummer's work (1968) was radiative
transfer in a plane-parallel layer with radiation sources both in a line spectrum
and in a continuous spectrum. In addition, the source of the line radiation in Hummer's work
contained some part due to the absorption of photons as a result of electron
collisions with the excited atom. The radiative transfer process in a medium
with non-resonant absorption in the case of partial frequency redistribution
was investigated both numerically and asymptotically in (Hummer & Kunasz 1980;
Frisch 1980),
where effective scaling laws were found for the case of small absorption
coefficients and large optical thicknesses of the layer.
In the present work, the transport equations have a somewhat different form, because
the only source of radiation in the UV lines is the spontaneous emission of the FeII
ions excited by the wide-band Ly![]() radiation at different wavelength.
Furthermore, the optical thickness
radiation at different wavelength.
Furthermore, the optical thickness
![]() of the
of the
![]() transition,
which is responsible for the intense UV radiation, is substantial
transition,
which is responsible for the intense UV radiation, is substantial
![]() (Johansson & Letokhov 2001b), but not so great that it is
necessary to take into account the scattering in the Lorentzian wings, i.e. the
parameter
(Johansson & Letokhov 2001b), but not so great that it is
necessary to take into account the scattering in the Lorentzian wings, i.e. the
parameter
![]() ,
where the damping parameter
,
where the damping parameter
![]() for the FeII lines of interest. And finally, the
geometry of the passive region of blob B exposed to the Ly
for the FeII lines of interest. And finally, the
geometry of the passive region of blob B exposed to the Ly![]() radiation is more spherical than plane, even though it is a convenient assumption
to simplify the calculations. Thus, for the present problem with the anomalous
Fe II lines it would be desirable
to calculate the radiative transfer in an optically dense medium
featuring nonresonant absorption in a spherical geometry.
radiation is more spherical than plane, even though it is a convenient assumption
to simplify the calculations. Thus, for the present problem with the anomalous
Fe II lines it would be desirable
to calculate the radiative transfer in an optically dense medium
featuring nonresonant absorption in a spherical geometry.
Copyright ESO 2002