5 Validation

To ensure that this program would work with our sample of A-F type stars, synthetic, Vega and solar spectra were used.

  
5.1 Comparison with another spectrum synthesis code

  

Table 2: Abundance determination for a synthetic spectrum computed with SYNSPEC and known abundances.

$${ \begin{tabular}{c r @{.}l r @{.} l} \hline Element & \mul... ...$-$6&01\\ Ni & $-$5 & 89 & $-$5&91\\ \hline \end{tabular}}$$

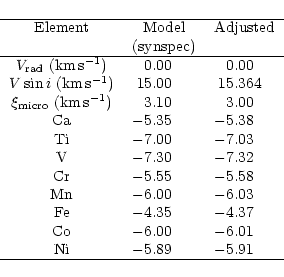
In order to check the modifications of the spectral synthesis part, a spectrum was produced using SYNSPEC (Hubeny et al. 1994) with a given model ( $T_{\rm eff} = 7500~{\rm K}$, $\log{g} = 4.0$), line list, abundances, radial and rotational velocities (see Table 2). The same input parameters were used to produce a spectrum with our code. Both codes give almost the same spectrum as can be judged by eye when looking at the ratio of both spectra. That validated the spectrum synthesis part.

In order to check the minimization routine, the spectrum from SYNSPEC was used as the one to be analyzed. Since the routine needs a starting point, solar abundances were used.

The agreement between the input and converged abundances is very good (see Table 2). The difference is always $\leq$0.03 dex. Moreover, all velocities ( $V_{\rm rad}, V\sin{i}, \xi_{\rm micro}$) were very well adjusted, even starting from very different values.

  
5.2 Vega

G.M. Hill provided us with a spectrum of Vega going from 4460 to 4530 Å, that was used to debug the modifications of the code. Then a spectrum was obtained with ELODIE. As there were a lot of changes, it is no longer possible to reproduce the abundances exactly as Hill's original program, essentially because of the change of the model atmosphere and lines list sources. However, the abundances estimated after the modifications are in agreement with the ones of HL93 within 0.2 dex except for Y where only one line was used.

For Vega, we used the model computed especially for this star by Kurucz and available on his web page http://cfaku5.harvard.edu/. This model is computed without convection and with stellar parameters as follows: $T_{\rm eff}=9400$K, $\log{g}=3.90$ and $\xi_{\rm micro}=0~{\rm km\,s^{-1}}$.

The whole procedure was run on the ELODIE spectrum and the results are given in Table 3.

   

Table 3: Derived abundances ( $\log{\left[\frac{N}{N_{\rm H}}\right]}$) and velocities $({\rm km\,s^{-1}})$ for Vega compared with works of HL93, Adelman & Gulliver (1990), Lemke (1989, 1990 and references therein), and Qiu et al. (2001).

Elt	Abund	HL93	Adelman	Lemke	Qiu
He	-1.36	-1.20	-1.52
C	-3.51	-3.53		-3.51	-3.54
O	-3.34				-2.99
Na	-5.69	<-5.1			-5.55
Mg	-4.84	-4.69	-5.09		-5.27
Si	-5.11	-5.14		-5.06	-5.04
Ca	-6.10	-6.11	-6.21	-6.18	-6.67
Sc	-9.58		-9.62		-9.67
Ti	-7.55	-7.36	-7.47	-7.50	-7.42
Cr	-6.91	-6.81	-6.76		-6.81
Fe	-5.14	-5.03	-5.08	-5.03	-5.07
Sr	-10.03	<-7.6		-9.93	-10.72
Y	-9.96	-10.38			-10.35
Ba	-10.51	-10.51	-10.58	-10.57	-11.19
$T_{\rm eff}$	9400	9560	9400	9500	9430
$\log{g}$	3.90	4.05	4.03	3.90	3.95
$V_{\rm rad}$	-13.25	-13.1	-13.26
$V\sin{i}$	23.2	22.4	22.4
$\xi_{\rm micro}$	1.9	1.0	0.6	2.0	1.5

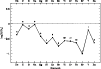Figure 7: Logarithmic abundances of Vega with respect to the Sun. The numbers indicate the numbers of lines with an equivalent width bigger that 10 mÅ.

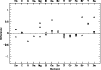Figure 8: Difference for Vega between this paper and different authors ($\times$ HL93, $\blacksquare$ Adelman, $\square$ Lemke, and $\vartriangle$ Qiu).

Our estimates are in good agreement with the values available from the literature (see Fig. 8 and Table 3). However, it is difficult to compare the abundance pattern for Vega directly because of the differences in the choice of fundamental parameters (see Table 3). For this star, a difference of some tenths of dex is not surprising. These differences are the main problem when it comes to compare results from different authors. Moreover, for some elements, only a few lines (sometimes only one, see number in Fig. 7) are available and it implies that these elements are much more sensitive to errors on the line parameters such as $\log{gf}$. Finally, in Vega, NLTE effects are not negligible for some elements. For example, a correction of 0.29 dex for barium was calculated by Gigas (1988). This paper is limited to LTE analysis, but it will be important to check for NLTE effects when looking for trends in element abundances.

  
5.3 The Sun

Even if it is not easy to compare studies of various authors on Vega, it has the advantage to be easy to observe and it is one of the "standard'' A0 stars even though it is underabundant. Moreover, the original spectrum synthesis code was intended for A-type stars so it is important to check its validity for cooler stars since we want to use it on F-type stars too. Therefore in order to carry out a much stronger comparison, a solar spectrum was used (see Sect. 2 for observation details). The solar spectrum is much more crowded than the Vega one. It is not always easy to find continuum points, and the abundance that will be determined will show not only whether our minimization method is efficient but also how well the continuum was placed. In any case, a careful comparison with the Solar Atlas was done on the whole spectral range. Figure 5 shows an example of the comparison on a small spectral range.

For the Sun, we computed a model with solar parameters ( $T_{\rm eff}=5777$ K, $\log{g}=4.44$ and $\xi_{\rm micro}=1~{\rm km\,s^{-1}}$) without overshooting.

As explained in Sect. 4.2.1, it was necessary to adjust some $\log{gf}$ values in order to get "canonical'' solar values for some elements. The biggest problem was with Si. A lot of its lines turned out to have intensities very different from the ones observed when computed with VALD $\log{gf}$ (for Vega, the only useful Si lines had correct gf values). Moreover, the errors were very important and could not come from a wrong placement of the continuum. One can wonder why the estimated Si abundance differs by more than 0.05 dex from the canonical one, while $\log{gf}$ values were adjusted. In fact, we tried to adjust as few lines as possible. It is always possible that small differences between observed and synthesized spectra result from unresolved lines or weak lines that are not in the line list and therefore not computed. A special care was brought in the computation of lines that were not strong enough in the computed spectrum to check how far a sum of weak lines might explain the gap. An interrogation of VALD around such lines was done, showing that the difference was never coming from forgotten lines.

Figure 9: Top: superposition of a part of the observed spectrum (thin line) and the synthetic one (thick line) for the Sun. Bottom: ratio synthetic to observed.

   

Table 4: Derived abundances for the Sun, difference with values from Grevesse & Sauval (1998) and number of lines with an equivalent width bigger than 10 mÅ.

Elt	Abundance	difference	# lines
	$\log{\left[\frac{N}{N_{\rm H}}\right]}+12$
C	8.56	0.04	3
Na	6.31	-0.02	18
Mg	7.52	-0.06	22
Al	6.42	-0.05	6
Si	7.48	-0.07	76
S	7.22	-0.11	3
Ca	6.34	-0.02	69
Sc	3.18	0.01	26
Ti	5.01	-0.01	361
V	4.04	0.04	87
Cr	5.71	0.04	368
Mn	5.49	0.10	81
Fe	7.52	0.02	1507
Co	4.91	-0.01	84
Ni	6.22	-0.03	292
Cu	4.23	0.02	5
Zn	4.69	0.09	3
Ga	2.84	-0.04	1
Sr	2.95	0.02	3
Y	2.20	-0.04	20
Zr	2.67	0.07	19
Ba	2.15	0.02	7
La	1.16	-0.01	5
Ce	1.66	0.08	20
Nd	1.56	0.06	12
Sm	1.08	0.07	3
Eu	0.55	0.04	2

Figure 10: Same as Fig. 7, but with the difference for the Sun between this paper and Grevesse & Sauval (1998).

In the solar case, the initial abundances were chosen different from the canonical one by some tenths of dex. The result of our analyzis is shown in Table 4 and in Fig. 10. A microturbulent velocity $\xi_{\rm micro}=0.79~{\rm km\,s^{-1}}$ was found, which is compatible with the value found by Blackwell et al. (1995, $\xi_{\rm micro}=0.775~{\rm km\,s^{-1}}$) when using the model from ATLAS9. Concerning the rotational velocities, it is important to note that the code does not implement macroturbulence treatment. Therefore, it is not possible to distinguish macroturbulent and rotational velocities. A value of $3.8~{\rm km\,s^{-1}}$ for the "rotational'' velocity was found. If we assume that the macroturbulence is isotropic, it is possible to get a more realistic value of the rotational velocity by doing a quadratic subtraction of the macroturbulent velocity. Takeda (1995b) found that the macroturbulence change from 2 to 4 $~{\rm km\,s^{-1}}$ depending of the choice of strong or weak lines. If we take a mean value of 3, we get $2.33~{\rm km\,s^{-1}}$ for the rotational velocity, which is slightly larger than the synodic value of $1.9~{\rm km\,s^{-1}}$.

The agreement for the abundances is always better than 0.1 dex except for S and Mn. The difference for S results from the value of $\log{\left[\frac{N({\rm el})}{N_{\rm H}}\right]}+12 = 7.33$ in Grevesse & Sauval (1998). However, both elements have photospheric abundances different from the meteoritic ones by as much as 0.1 dex. The meteoritic abundances are 7.20 and 5.53 for S and Mn respectively. Moreover, Rentzsch-Holm (1997) found an abundance of 7.21 for S, and in previous papers of Anders & Grevesse (1989), the S abundance is also 7.21, which is in perfect agreement with our value. Finally, the line list contains only 3 weak lines of about 15 mÅ, and therefore very sensitive to the continuum. Let us just stress that we do not maintain that our value is the correct one, but that for this element, the uncertainty is high. Concerning Mn, our value is close to the meteoritic value too. On the other hand, hyperfine splitting can have a significant impact and may lead to abundance overestimate of about 0.1 dex.