

Up: Automated spectroscopic abundances of
Subsections
This section presents the method for abundance analysis. In
the first part (Sect. 4.1), the spectrum synthesis
program is described. In the second (Sect. 4.2), the
minimization method is explained.
This method adjusts the
abundances using synthetic spectra. The starting point was the program
described in Hill & Landstreet (1993), which was used to determine
detailed abundances in A-type stars and has been kindly provided by
Dr. G. M. Hill. The modifications made to this
program will be presented in this section.
4.1 spectrum synthesis
The spectral synthesis code used here is similar to the one described in
HL93. It is an LTE synthesis code (see HL93 for details). Various
modifications were done:
-
The code from HL93 used the model atmospheres ATLAS5 of Kurucz
(1979). It was modified to allow the use of ATLAS9
models. However, the format of the models has changed. In ATLAS5,
there was a column containing the geometrical depth X and another
containing the optical depth at 5000 Å,
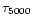 ,
and the
code of HL93 uses it to compute the optical depth at each wavelength of
the spectrum (
,
and the
code of HL93 uses it to compute the optical depth at each wavelength of
the spectrum (
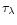 ). However, in ATLAS9 the depth is only
given in the
"rhox'' parameter which is the
density integrated as far as the geometrical depth X. In order to modify
the code as little as possible, we only changed the way
). However, in ATLAS9 the depth is only
given in the
"rhox'' parameter which is the
density integrated as far as the geometrical depth X. In order to modify
the code as little as possible, we only changed the way
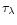 is computed. A subroutine of the ADRS code
(Y. Chmielewski 2000) was used to reformat the model as a
function of
is computed. A subroutine of the ADRS code
(Y. Chmielewski 2000) was used to reformat the model as a
function of
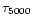 .
Then it was easy to use
.
Then it was easy to use
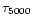 instead of X and the following
equation was used for the calculation of the optical depth at each
wavelength step.
instead of X and the following
equation was used for the calculation of the optical depth at each
wavelength step.
ATLAS9 was installed on a SunBlade100 computer (Sun UltraSparcII
machine). The Unix version adapted by M. Lemke![[*]](/icons/foot_motif.gif) was used
because the version of Kurucz (1993) is adapted to
VAX-VMS. It will allow to compute models with the right effective
temperature, gravity, metallicity and microturbulent
velocity. Models will be computed without overshooting as it appears
that they are best adapted to abundances
analysis (see for example Castelli et al. 1996);
was used
because the version of Kurucz (1993) is adapted to
VAX-VMS. It will allow to compute models with the right effective
temperature, gravity, metallicity and microturbulent
velocity. Models will be computed without overshooting as it appears
that they are best adapted to abundances
analysis (see for example Castelli et al. 1996);
-
The second modification allows the use of the VALD database (Piskunov
et al. 1995, Kupka et al. 1999 and Ryabchikova et al. 1999 ) as the source
of line list parameters. This
database provides
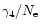 and
and
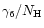 at 10000 K for the Stark and van der Waals
damping parameters respectively instead of C4 and C6 used by HL93.
In case these values are not available, the damping parameters are
calculated using the formulae described in HL93;
at 10000 K for the Stark and van der Waals
damping parameters respectively instead of C4 and C6 used by HL93.
In case these values are not available, the damping parameters are
calculated using the formulae described in HL93;
-
The polynomial partition functions were completed for
as many elements as possible, using data from Irwin
(1981) and Sauval & Tatum (1984). In case that the
function is unavailable, the program uses the statistical weight of the
lowest energy level. However, for some elements like Co and Ba, using
a partition function or the approximate value may result in abundance
changes as high as 0.2 dex;
- Finally, there were several other changes, including the introduction
of dynamical memory allocation. However, the theoretical
assumptions used in the initial code do not change.
4.2 Abundances determination
4.2.1 Line list
Instead of using a set of meticulously selected lines, the first
hope was to use the line list as it comes from the VALD database, using
the "extract stellar'' option. This choice was motivated by the large
spectral range of ELODIE. The idea was to use a large number of lines
with parameters not necessarily well known, but considering a
large number, the effect of poor 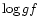 should
disappear and the mean value for an element should be
correct. This idea is justified for elements of the iron peak, but not
for elements as Si, Sr, Ba, and heavier
elements. For these elements (except
for Si), only one or a few lines are present, and it is easy to understand
that if there are
only a few lines, the abundance is very sensitive to the line
parameters.
should
disappear and the mean value for an element should be
correct. This idea is justified for elements of the iron peak, but not
for elements as Si, Sr, Ba, and heavier
elements. For these elements (except
for Si), only one or a few lines are present, and it is easy to understand
that if there are
only a few lines, the abundance is very sensitive to the line
parameters.
Although VALD-2 provides the most recent collection of oscillator
strength data, it appears that for some elements with few lines (and Si),
the 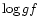 values had to be examined
individually and adjusted whenever possible (i.e. when the line was
not blended). To achieve good adjustment, lines of problematic elements
were checked individually and 2 methods were used to adjust the
oscillator strength using the Sun spectrum:
values had to be examined
individually and adjusted whenever possible (i.e. when the line was
not blended). To achieve good adjustment, lines of problematic elements
were checked individually and 2 methods were used to adjust the
oscillator strength using the Sun spectrum:
-
The line was checked for presence in the line list coming from
the SPECTRUM package of
Gray (1994, and available at http://www.phys.appstate.edu/spectrum/spectrum.html) that contains
adjusted
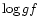 for some lines. If such was the case, and if the
value was different, this value was tried. Then if it gave good results
it was retained;
for some lines. If such was the case, and if the
value was different, this value was tried. Then if it gave good results
it was retained;
-
In case of failure of the first method, the value was adjusted on the
Solar spectrum with an
iterative procedure until the abundance was correct within 0.05 dex.
Finally, instead of using directly the VALD result, a
reference line list covering our spectral domain was compiled, and
used for all the stars to be analyzed. It is
to be noticed that this line list may still contain erroneous 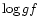 values
because every line is not necessarily visible in the solar spectrum, and also
because this parameter was only adjusted for problematic elements when
the line was clearly
identifiable. Moreover, lines can be individually erroneous, but when
all lines of an element are used together, the individual errors
seems to cancel out. This is the case in particular for iron where
statistically, the abundance is correct while a lot of lines have
inaccurate
values
because every line is not necessarily visible in the solar spectrum, and also
because this parameter was only adjusted for problematic elements when
the line was clearly
identifiable. Moreover, lines can be individually erroneous, but when
all lines of an element are used together, the individual errors
seems to cancel out. This is the case in particular for iron where
statistically, the abundance is correct while a lot of lines have
inaccurate 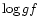 values. For other elements, it is not
obvious that these errors should average, but the application of the
method for the Sun seems to indicate that it is the case
(see Sect. 5.3).
values. For other elements, it is not
obvious that these errors should average, but the application of the
method for the Sun seems to indicate that it is the case
(see Sect. 5.3).
The program of HL93 uses the technique known as "downhill simplex
method''. This method is certainly the best if the goal is
"to get something working quickly'', in the sense that it does not have
strong initial constraints. Another advantage is that it does
not require derivatives. However, it is not the fastest
one. Moreover, in our case, the function to be evaluated requires
computation of a synthetic spectrum. The major improvement in time will come
from lowering the number of spectra to be computed. Looking for
minimization methods of multidimensional functions in
"Numerical Recipes'' (Press et al. 1992), we
decided to implement a direction set method in multidimensions known
as Powell's method. This method can be summarized as
follows. Given a set of N directions (where N is the number of free variables), the method
performs a quadratic minimization along each direction and tries to
define a new one as the direction of the largest
decrease. We simply adapt the Numerical Recipies code by
adding some tests to avoid looping that may
occur if the program tries to adjust lines of an element that are too
faint to be of any significance.
Initial conditions: in order to use this method an initial set of
directions has to be defined. The goal is to
adjust radial, rotational and microturbulent velocities as well as
abundances. In order to be efficient even in the first iteration,
it appears that the best choice of directions is to adjust
successively radial velocity (which is fixed when it is available from
ELODIE online
reduction), rotational velocity,
the abundances starting from the element with the maximum of
significant lines, and finally microturbulent velocity.
As we do not know a priori the abundance pattern, the starting
point is the solar one. Note that the solar abundances will always
refer to Grevesse & Sauval (1998). The order proposed is
justified by the following example.
Let us consider a blend of two lines of different elements;
the element with the largest number of lines will be adjusted
first. As it has other lines, it is less sensitive to the blend and
the program does not try to fill the blend by increasing the abundance
of this element only, as it would happen if the element with only one
or two lines was adjusted first. Then
the second element is adjusted in order to fill up the blend.
Procedure of analysis: it is important to retain only the lines from the reference list
that contribute to the spectrum.
Therefore lines were sorted using the
equivalent width computed with a reduced version of the program. Only
lines with an equivalent width larger than 10 mÅ (when computed with
an atmosphere model corresponding to the stellar parameters and solar
abundances) are used for the first abundance determination. The results
of this first minimization are used to re-sort out
the lines with the same equivalent width criterion. Then a second
computation is done with the new line list, using the result of the
first computation as a starting point for the velocities and
abundances. That speeds up the second adjustment.
This analysing procedure allows to
eliminate a lot of lines that are significant for
solar abundances but are no longer visible when it comes to abundances
of the star. Conversely, it may also allow to gain lines that were
too weak for solar abundances but are strong enough with the stellar
value.
Speed optimization: during abundance analysis, a synthetic spectrum is computed at each
step of the minimization procedure. It is important to find a way
to reduce the time of analysis as much as possible.
The spectral range of ELODIE is wide (3900-6820 Å). In order to have
the best possible abundance estimates, it is important to use the
largest number of lines i.e. the widest possible spectral
range. However it is not possible, with this
method, to use the whole spectral range at once for various reasons:
-
The program does not implement the computation of Balmer lines because
HL93 only used small spectral windows. It
only implements H
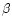 but this
line is just treated as a correction to the continuum. The other Balmer
lines are not computed. Only H
but this
line is just treated as a correction to the continuum. The other Balmer
lines are not computed. Only H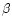 was included by HL93 because the HeI
was included by HL93 because the HeI
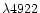 line lies in its red wing, and it was an important line
for the stars they studied;
line lies in its red wing, and it was an important line
for the stars they studied;
-
Running the program on a spectrum from 5000 to 6500 is much slower
than adjusting 4 parts of 400 Å successively on the same
computer. This is surprising, but may come from inadequate
programming as would be the case if looping in an array using the bad
order of indices (one index is going much faster than another);
-
The memory used by the program has to be kept within reasonable values
because it is important to be able to dispatch the task on a large number of
computers as the sample of stars to study is large. However if the
required memory is too large, the use of a given computer is no longer
possible or the program has to be stopped during working
hours
![[*]](/icons/foot_motif.gif) ;
;
- Because of the strong lines of hydrogen and calcium and the resulting
shape of the spectrum in the range 3900 to 4100 Å(see
Fig. 3), it is very difficult to define the continuum
there. The difficulty is enhanced by the small efficiency of ELODIE in
the blue.
Therefore the spectra were cut in the 7 parts defined in
Table 1.
Table 1:
Definition of the 7 parts in Å.
| spectral range |
| 4125-4300 |
| 4400-4800 |
| 4950-5300 |
| 5300-5700 |
| 5700-6100 |
| 6100-6500 |
| 6580-6820 |
![\begin{figure}
\par\includegraphics[width=16.3cm]{1986f6.eps}
\end{figure}](/articles/aa/full/2002/07/aa1986/Timg32.gif) |
Figure 6:
Top: superposition of a part of the observed spectrum
(thin line)
and the synthetic one (thick line) for Vega. The atomic numbers and
ionization stages (1 for singly ionized) of the species are indicated
under the lines. Bottom: ratio
synthetic to observed. |
Working with 7 parts, however, implies that we have 7 different
estimates for each
abundance. The final abundance is obtained by a weighted mean of the
7 individual estimates. Each individual value is weighted by the number of
lines having a synthetic equivalent width larger than 10 mÅ.
It is important to note that telluric lines were not corrected for before
analysis. Two of the seven parts contain a large number of these
lines. They are the two parts going from 5700 to 6500 Å. It
appears that given the width of the parts, there are enough lines for
each element so that the minimization routine is not
misled by the telluric lines. The exception may come in some slowly
rotating stars from elements with only one or two lines which are well
superposed with telluric lines.
Finally, it appears that this method is much more efficient than the
downhill simplex one when it comes to adjust abundances of
element with only a few lines. In the first iteration, the
abundance of each element is adjusted in turn even if the
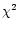 value does not change a lot, whereas with the downhill
simplex method, a step in the direction of an element with only a
few lines
is unlikely. Moreover, it takes less
computer time. One reason is that a test was added to the
minimization routine so that an element, the abundance of which does
not change by more than 0.1% in two
successive iterations, is no longer adjusted.
value does not change a lot, whereas with the downhill
simplex method, a step in the direction of an element with only a
few lines
is unlikely. Moreover, it takes less
computer time. One reason is that a test was added to the
minimization routine so that an element, the abundance of which does
not change by more than 0.1% in two
successive iterations, is no longer adjusted.


Up: Automated spectroscopic abundances of
Copyright ESO 2002
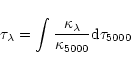
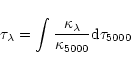
![]() should
disappear and the mean value for an element should be
correct. This idea is justified for elements of the iron peak, but not
for elements as Si, Sr, Ba, and heavier
elements. For these elements (except
for Si), only one or a few lines are present, and it is easy to understand
that if there are
only a few lines, the abundance is very sensitive to the line
parameters.
should
disappear and the mean value for an element should be
correct. This idea is justified for elements of the iron peak, but not
for elements as Si, Sr, Ba, and heavier
elements. For these elements (except
for Si), only one or a few lines are present, and it is easy to understand
that if there are
only a few lines, the abundance is very sensitive to the line
parameters.
![]() values had to be examined
individually and adjusted whenever possible (i.e. when the line was
not blended). To achieve good adjustment, lines of problematic elements
were checked individually and 2 methods were used to adjust the
oscillator strength using the Sun spectrum:
values had to be examined
individually and adjusted whenever possible (i.e. when the line was
not blended). To achieve good adjustment, lines of problematic elements
were checked individually and 2 methods were used to adjust the
oscillator strength using the Sun spectrum:
![]() value does not change a lot, whereas with the downhill
simplex method, a step in the direction of an element with only a
few lines
is unlikely. Moreover, it takes less
computer time. One reason is that a test was added to the
minimization routine so that an element, the abundance of which does
not change by more than 0.1% in two
successive iterations, is no longer adjusted.
value does not change a lot, whereas with the downhill
simplex method, a step in the direction of an element with only a
few lines
is unlikely. Moreover, it takes less
computer time. One reason is that a test was added to the
minimization routine so that an element, the abundance of which does
not change by more than 0.1% in two
successive iterations, is no longer adjusted.