

Up: Stationary equatorial MHD flows
Subsections
4 Efficiency of the magnetic to kinetic energy transfer
To study the efficiency of the winds computed in the previous section,
we need to express the different components of the energy flux along
the flow:
Notice that the matter part is made up of the rest-mass, kinetic and
internal energy of the matter. We define two parameters: the initial
baryonic load 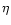
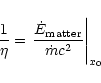 |
(73) |
and the ratio of the initial power injected in the electromagnetic
field over the initial power injected in the matter
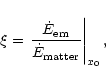 |
(74) |
where x0 is the radius where the wind starts. The value of 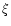 depends only weakly on x0, and we have arbitrary chosen x0=6m(or r0=6rg). One sees that
depends only weakly on x0, and we have arbitrary chosen x0=6m(or r0=6rg). One sees that 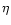 will be fixed by
will be fixed by 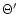 [via
the initial value of
[via
the initial value of
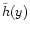 ]
whereas
]
whereas 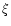 depends strongly on
depends strongly on
 .
Along the flow, the internal energy is converted into
kinetic energy which accelerates the wind. Therefore if there were no
magnetic field, the Lorentz factor at infinity would be
.
Along the flow, the internal energy is converted into
kinetic energy which accelerates the wind. Therefore if there were no
magnetic field, the Lorentz factor at infinity would be
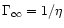 .
However, the magnetic field can also
contribute to the acceleration (when coupled with the rotation) and
depending on the efficiency of the conversion of electromagnetic into
kinetic energy, the terminal Lorentz factor can be larger than
.
However, the magnetic field can also
contribute to the acceleration (when coupled with the rotation) and
depending on the efficiency of the conversion of electromagnetic into
kinetic energy, the terminal Lorentz factor can be larger than
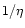 ,
with a maximum value (complete conversion) given by
,
with a maximum value (complete conversion) given by
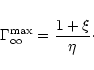 |
(75) |
In reality the conversion will never be complete and will be estimated
by the following fraction
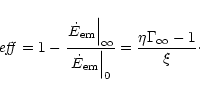 |
(76) |
In the pressureless case (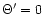 )
it is well known that the
magnetic to kinetic energy transfer is very inefficient for high
terminal Lorentz factors (Michel 1969)
)
it is well known that the
magnetic to kinetic energy transfer is very inefficient for high
terminal Lorentz factors (Michel 1969)
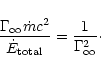 |
(77) |
The curves for constant terminal Lorentz factor in
Fig. 3 show clearly that for highly relativistic
winds (
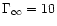 ,
100 and 1000) the terminal Lorentz
factor
,
100 and 1000) the terminal Lorentz
factor
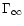 is independent of
is independent of 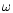 (or equivalently of
(or equivalently of
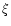 )
which means that there can only be a tiny magnetic to kinetic
energy conversion. When
)
which means that there can only be a tiny magnetic to kinetic
energy conversion. When 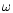 is very close to the maximal allowed
value and the outflow is Poynting flux dominated (corresponding to the
case where the Alfvén point is at the light surface radius) this
tendency is not valid anymore. In this region the terminal Lorentz
factor
is very close to the maximal allowed
value and the outflow is Poynting flux dominated (corresponding to the
case where the Alfvén point is at the light surface radius) this
tendency is not valid anymore. In this region the terminal Lorentz
factor
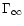 depends strongly on
depends strongly on 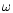 and is almost
independent of
and is almost
independent of 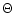 (or equivalently of
(or equivalently of 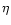 ). However, even in
this case only a tiny fraction of the magnetic energy is converted
into kinetic energy. The converted energy amount is great compared to
the initial energy in the matter part and therefore leads to a greater
increase in
). However, even in
this case only a tiny fraction of the magnetic energy is converted
into kinetic energy. The converted energy amount is great compared to
the initial energy in the matter part and therefore leads to a greater
increase in 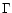 and
and
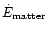 throughout the flow.
The efficiency
throughout the flow.
The efficiency
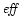 of the conversion is maximal in the
pressureless case (
of the conversion is maximal in the
pressureless case (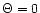 )
but is still rather small. In this
case the parameters
)
but is still rather small. In this
case the parameters 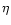 and
and 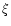 are given by
are given by
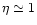 and
and
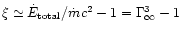 which corresponds to
which corresponds to
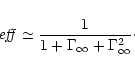 |
(78) |
These tendencies are still present in mildly relativistic winds, as
can be seen in Fig. 3 for
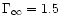 where
we have indicated the evolution of
where
we have indicated the evolution of
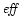 along the curve. It
is only within the classical limit that the conversion becomes
important. This is shown in Fig. 3 (The case
along the curve. It
is only within the classical limit that the conversion becomes
important. This is shown in Fig. 3 (The case
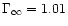 (
(
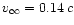 )). Here the efficiency of
conversion reaches
)). Here the efficiency of
conversion reaches 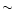 60% in the pressureless case, which is in
agreement with the classical study of Sakurai (1985).
60% in the pressureless case, which is in
agreement with the classical study of Sakurai (1985).
All wind solutions showing (except in the classical limit) a very bad
efficiency of the electromagnetic to kinetic energy conversion have
been calculated for a particular geometry corresponding to
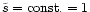 in our dimensionless units. This
corresponds to magnetic flux tubes of constant opening angle. Under
the assumption that the velocity is purely radial and constant at
infinity it is possible to predict analytically the asymptotic
behavior of the flow for any kind of geometry
in our dimensionless units. This
corresponds to magnetic flux tubes of constant opening angle. Under
the assumption that the velocity is purely radial and constant at
infinity it is possible to predict analytically the asymptotic
behavior of the flow for any kind of geometry
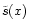 :
:
so that the asymptotic expressions of the energy fluxes are
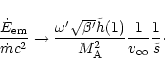 |
(80) |
From the last equation, one sees that the magnetic to kinetic energy
conversion depends strongly on 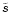 .
At infinity
.
At infinity
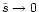 is unphysical because it would mean that the energy diverges. The
case where the opening angle is constant at infinity corresponds to
is unphysical because it would mean that the energy diverges. The
case where the opening angle is constant at infinity corresponds to
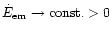 at infinity so that the
conversion is not complete and the case where the opening angle
diverges (
at infinity so that the
conversion is not complete and the case where the opening angle
diverges (
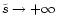 )
gives
)
gives
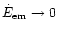 so
that the conversion is complete. These results indicate that all
models considered in the previous section are inefficient due to a
particular choice of the geometry:
so
that the conversion is complete. These results indicate that all
models considered in the previous section are inefficient due to a
particular choice of the geometry:
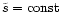 .
This
assumption is certainly correct at very large distance from the source
but the opening angle may have variations at smaller radii.
Equation (80) indicates that every region where the
opening angle increases is a region of efficient magnetic to kinetic
energy transfer. This is in agreement with the results of
Begelman & Li (1994).
.
This
assumption is certainly correct at very large distance from the source
but the opening angle may have variations at smaller radii.
Equation (80) indicates that every region where the
opening angle increases is a region of efficient magnetic to kinetic
energy transfer. This is in agreement with the results of
Begelman & Li (1994).
To check that the geometry is really the key parameter governing the
efficiency of such winds we have computed some models using various
laws for the evolution of the opening angle
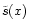 .
The
results are shown in Fig. 4 and confirm the previous
analysis. We have considered a Schwarzschild metric with m=0.01 and
a wind model characterized by
.
The
results are shown in Fig. 4 and confirm the previous
analysis. We have considered a Schwarzschild metric with m=0.01 and
a wind model characterized by
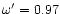 and
and
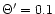 (so the
energy flux is initially dominated by the electromagnetic energy
flux). We plot the different energy fluxes and the "Lorentz
factor
(so the
energy flux is initially dominated by the electromagnetic energy
flux). We plot the different energy fluxes and the "Lorentz
factor![[*]](/icons/foot_motif.gif) ''
''
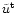 as well as the geometrical function
as well as the geometrical function
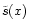 we have used in each case. Figure 4a
corresponds to the inefficient case
we have used in each case. Figure 4a
corresponds to the inefficient case
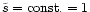 .
Figure 4b corresponds to the case where
.
Figure 4b corresponds to the case where 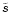 increases in a region located between x1=10 and x2=18: the
magnetic to kinetic energy conversion is immediately better. The
efficiency
increases in a region located between x1=10 and x2=18: the
magnetic to kinetic energy conversion is immediately better. The
efficiency
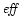 increases also in geometries with different
shapes (Figs. 4d, f, g, h) and different locations of the
increases also in geometries with different
shapes (Figs. 4d, f, g, h) and different locations of the
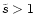 -region, provided that this region lies beyond the fast
point as shown by Begelman & Li (1994). In this case
-region, provided that this region lies beyond the fast
point as shown by Begelman & Li (1994). In this case
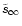 is the only relevant quantity which governs
is the only relevant quantity which governs
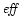 .
A
.
A
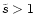 -region within the fast point like in
Fig. 4e does not increase
-region within the fast point like in
Fig. 4e does not increase
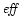 and is similar
to the purely radial case.
and is similar
to the purely radial case.
![\begin{figure}
\par\includegraphics[height=10cm,width=18cm,clip]{h2857f4} \end{figure}](/articles/aa/full/2002/03/aah2857/Timg298.gif) |
Figure 4:
Effect of the geometry on the efficiency of the
magnetic to kinetic energy conversion: we consider a
Schwarzschild metric with m=0.01 and a wind solution
characterized by
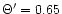 and
and
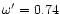 .
This
corresponds to an initial energy flux which is dominated by the
electromagnetic part: .
This
corresponds to an initial energy flux which is dominated by the
electromagnetic part: 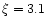 for all models so that initially
for all models so that initially
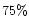 of the energy is magnetic. All solutions presented here
have
of the energy is magnetic. All solutions presented here
have
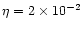 except for cases e) (
except for cases e) (
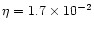 )
and h) ( )
and h) (
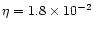 ). The slow and fast critical points are
located at ). The slow and fast critical points are
located at
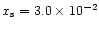 and
and
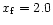 except for cases d)
(
except for cases d)
(
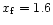 )
and h) ( )
and h) (
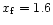 ). On each figure ). On each figure
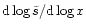 , ,
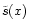 and
the different components of the energy flux (matter/em and total)
are presented as functions of the radius x. The "Lorentz
factor''
and
the different components of the energy flux (matter/em and total)
are presented as functions of the radius x. The "Lorentz
factor''
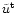 is also shown (dotted line). Three
vertical dotted lines show the location of the slow (s), the
Alfvén (A) and the fast point (f). Case a)
is also shown (dotted line). Three
vertical dotted lines show the location of the slow (s), the
Alfvén (A) and the fast point (f). Case a)
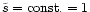 .
For this particular choice of the
geometry, the conversion is extremely inefficient
( .
For this particular choice of the
geometry, the conversion is extremely inefficient
(
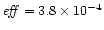 )
and the terminal Lorentz factor
equals )
and the terminal Lorentz factor
equals
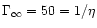 .
Case b) .
Case b) 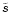 increases between x1=10 and x2=18 reaching a maximal
slope
increases between x1=10 and x2=18 reaching a maximal
slope
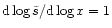 .
The
efficiency improves a lot: .
The
efficiency improves a lot:
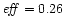 and
and
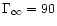 .
Case c) same as b) but .
Case c) same as b) but 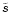 increases between
x1=1000 and
x2=1800 (
x2/x1 is
the same). It changes neither the efficiency nor the terminal
Lorentz factor. Case d) same as b) but
increases between
x1=1000 and
x2=1800 (
x2/x1 is
the same). It changes neither the efficiency nor the terminal
Lorentz factor. Case d) same as b) but 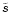 increases between x1=1.5 and x2=2.7 (
x2/x1 is
the same), i.e. before the position of the fast point in the
reference solution a). Again the efficiency
increases between x1=1.5 and x2=2.7 (
x2/x1 is
the same), i.e. before the position of the fast point in the
reference solution a). Again the efficiency
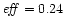 and the terminal Lorentz factor
and the terminal Lorentz factor
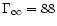 are almost
unchanged. Notice that the fast critical point has moved to be
almost at x1. Case e) same as b) but
are almost
unchanged. Notice that the fast critical point has moved to be
almost at x1. Case e) same as b) but 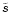 increases between x1=0.1 and
x2=0.18 (
x2/x1 is
the same), i.e. before the Alfvén point. The efficiency is
again very low:
increases between x1=0.1 and
x2=0.18 (
x2/x1 is
the same), i.e. before the Alfvén point. The efficiency is
again very low:
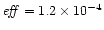 and
and
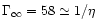 .
Case f) same as b) but
with a maximal slope of .
Case f) same as b) but
with a maximal slope of
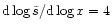 .
The efficiency is
better: .
The efficiency is
better:
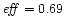 and
and
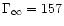 .
Case g) same as b) but the region where .
Case g) same as b) but the region where 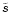 increases is larger: x1=10 and x2=100. Again the
efficiency is better:
increases is larger: x1=10 and x2=100. Again the
efficiency is better:
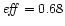 and
and
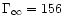 .
Case h) we have considered a case
where .
Case h) we have considered a case
where 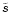 increases from x1=0.1 to
x2=104 with a maximal slope
increases from x1=0.1 to
x2=104 with a maximal slope
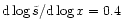 .
Almost 90%
of the magnetic energy is converted into kinetic energy
( .
Almost 90%
of the magnetic energy is converted into kinetic energy
(
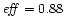 )
so that )
so that
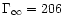 . . |
![\begin{figure}
\par\includegraphics[width=7.4cm,clip]{h2857f5} \end{figure}](/articles/aa/full/2002/03/aah2857/Timg299.gif) |
Figure 5:
The influence of the geometry, gravitation and
thermal energy upon the electromagnetic energy conversion. The
solid, dotted and dashed lines correspond to different
gravitational field strengths, m=0.001, m=0.01 and m=0.1.
a) The case for
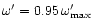 , ,
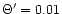 which is a cold Poynting-flux dominated outflow.
b) Thermal energy dominated fireball:
which is a cold Poynting-flux dominated outflow.
b) Thermal energy dominated fireball:
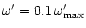 , ,
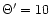 .
The dotted
line lies very close to the solid line and is not visible.
c) Non-relativistic case where the rest mass dominates
with .
The dotted
line lies very close to the solid line and is not visible.
c) Non-relativistic case where the rest mass dominates
with
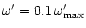 , ,
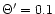 . . |
Begelman & Li (1994) showed that the electromagnetic energy flux
decreases like
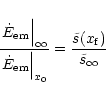 |
(81) |
for a cold flow in Minkowski metric. If the asymptotic regime is
already reached in the region where the opening angle increases,
Eq. (80) shows that this relation should still be valid in
the most general case, independent of the gravitational field or of
the initial amount of thermal energy. To check the validity of this
result we consider 9 different
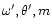 combinations,
illustrating all possible situations and for each of them we compute
the evolution of the efficiency when varying
combinations,
illustrating all possible situations and for each of them we compute
the evolution of the efficiency when varying
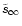 .
As
Fig. 4 shows, the exact shape of the geometry is not
important, so we adopt a particular choice where
.
As
Fig. 4 shows, the exact shape of the geometry is not
important, so we adopt a particular choice where 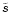 rises
from
rises
from
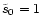 to
to
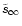 between x1=100 and
x2=200. This region lies always in the super-Alfvénic region,
which as discussed above is the condition for magnetic to kinetic
energy conversion. Figure 5 shows the quantity
between x1=100 and
x2=200. This region lies always in the super-Alfvénic region,
which as discussed above is the condition for magnetic to kinetic
energy conversion. Figure 5 shows the quantity
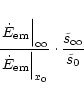 |
(82) |
plotted over
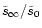 for the 9 different
cases. Notice that with our choice of geometry
for the 9 different
cases. Notice that with our choice of geometry
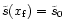 .
One sees that gravity and
pressure changes the simple picture a bit. In the cold cases
(Figs. 5a and c) the converted
energy fraction decreases for a stronger gravitational field and high
values of m. On the other hand the gravitational field increases
the energy conversion by a small amount in the hot thermal dominated
case as seen in Fig. 5b. But (81)
remains still valid within a factor of 2. For the cases of low
gravity and low thermal energy (solid lines in Figs. 5a
and c) the quantity (82) approaches 1as expected.
.
One sees that gravity and
pressure changes the simple picture a bit. In the cold cases
(Figs. 5a and c) the converted
energy fraction decreases for a stronger gravitational field and high
values of m. On the other hand the gravitational field increases
the energy conversion by a small amount in the hot thermal dominated
case as seen in Fig. 5b. But (81)
remains still valid within a factor of 2. For the cases of low
gravity and low thermal energy (solid lines in Figs. 5a
and c) the quantity (82) approaches 1as expected.
We can therefore conclude that the flow geometry always
dominates the energy conversion and all other parameters play an only
minor role.


Up: Stationary equatorial MHD flows
Copyright ESO 2002
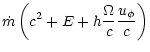
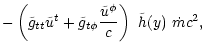
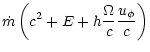
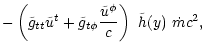
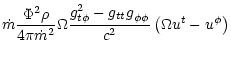
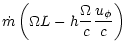
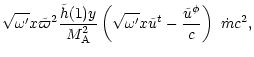
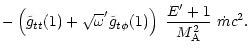
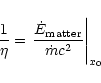
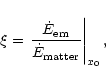
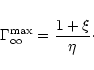
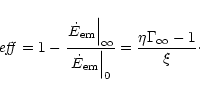
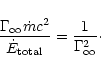
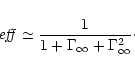
![]() in our dimensionless units. This
corresponds to magnetic flux tubes of constant opening angle. Under
the assumption that the velocity is purely radial and constant at
infinity it is possible to predict analytically the asymptotic
behavior of the flow for any kind of geometry
in our dimensionless units. This
corresponds to magnetic flux tubes of constant opening angle. Under
the assumption that the velocity is purely radial and constant at
infinity it is possible to predict analytically the asymptotic
behavior of the flow for any kind of geometry
![]() :
:
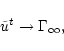
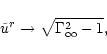
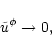
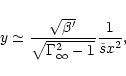
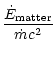
![]() .
The
results are shown in Fig. 4 and confirm the previous
analysis. We have considered a Schwarzschild metric with m=0.01 and
a wind model characterized by
.
The
results are shown in Fig. 4 and confirm the previous
analysis. We have considered a Schwarzschild metric with m=0.01 and
a wind model characterized by
![]() and
and
![]() (so the
energy flux is initially dominated by the electromagnetic energy
flux). We plot the different energy fluxes and the "Lorentz
factor
(so the
energy flux is initially dominated by the electromagnetic energy
flux). We plot the different energy fluxes and the "Lorentz
factor![]() ''
''
![]() as well as the geometrical function
as well as the geometrical function
![]() we have used in each case. Figure 4a
corresponds to the inefficient case
we have used in each case. Figure 4a
corresponds to the inefficient case
![]() .
Figure 4b corresponds to the case where
.
Figure 4b corresponds to the case where ![]() increases in a region located between x1=10 and x2=18: the
magnetic to kinetic energy conversion is immediately better. The
efficiency
increases in a region located between x1=10 and x2=18: the
magnetic to kinetic energy conversion is immediately better. The
efficiency
![]() increases also in geometries with different
shapes (Figs. 4d, f, g, h) and different locations of the
increases also in geometries with different
shapes (Figs. 4d, f, g, h) and different locations of the
![]() -region, provided that this region lies beyond the fast
point as shown by Begelman & Li (1994). In this case
-region, provided that this region lies beyond the fast
point as shown by Begelman & Li (1994). In this case
![]() is the only relevant quantity which governs
is the only relevant quantity which governs
![]() .
A
.
A
![]() -region within the fast point like in
Fig. 4e does not increase
-region within the fast point like in
Fig. 4e does not increase
![]() and is similar
to the purely radial case.
and is similar
to the purely radial case.