Since the discovery of their optical afterglows gamma-ray bursts
(hereafter GRBs) have been known to be located at cosmological
distance. More than ten redshifts have been measured from z=0.43(GRB990712) to z=4.5 (GRB000131). The corresponding radiated
energy in the gamma-ray domain (20-20000keV) ranges from
![]() erg (GRB970228) to
erg (GRB970228) to
![]() erg
(GRB990123) assuming isotropic emission. Most sources that have
been proposed to explain such a huge release of energy in a few
seconds involve a rapidly rotating compact stellar-mass core. Among
them the two most popular are mergers of compact objects (neutron
stars binary or neutron star - black hole systems) or collapses of
very massive stars to a black hole (collapsars)
(Mészáros & Rees 1992; Narayan et al. 1992; Mochkovitch et al. 1993; Woosley 1993; Paczynski 1998).
In both cases, the resulting system is a stellar mass black hole
surrounded by a thick torus made of stellar debris or of infalling
stellar material partially supported by centrifugal forces. An other
interesting proposition (Usov 1992; Kluzniak & Ruderman 1998; Spruit 1999)
associates GRBs with highly magnetized millisecond pulsars. The
location of the detected optical counterparts, well inside their host
galaxy and possibly associated with star-forming regions, seems to
favor the collapsar scenario. However the other propositions cannot be
ruled out, at least for short bursts, for which no optical counterpart
has been detected yet.
erg
(GRB990123) assuming isotropic emission. Most sources that have
been proposed to explain such a huge release of energy in a few
seconds involve a rapidly rotating compact stellar-mass core. Among
them the two most popular are mergers of compact objects (neutron
stars binary or neutron star - black hole systems) or collapses of
very massive stars to a black hole (collapsars)
(Mészáros & Rees 1992; Narayan et al. 1992; Mochkovitch et al. 1993; Woosley 1993; Paczynski 1998).
In both cases, the resulting system is a stellar mass black hole
surrounded by a thick torus made of stellar debris or of infalling
stellar material partially supported by centrifugal forces. An other
interesting proposition (Usov 1992; Kluzniak & Ruderman 1998; Spruit 1999)
associates GRBs with highly magnetized millisecond pulsars. The
location of the detected optical counterparts, well inside their host
galaxy and possibly associated with star-forming regions, seems to
favor the collapsar scenario. However the other propositions cannot be
ruled out, at least for short bursts, for which no optical counterpart
has been detected yet.
Whatever the source is, the released energy must initially be injected
in a wind which eventually becomes relativistic. The existence of such
a relativistic wind has been directly inferred from the observations
of radio scintillation in GRB970508 (Frail et al. 1997) and is also
needed to avoid photon-photon annihilation. The absence of signature
of this last process in the BATSE spectra of GRBs implies very high
Lorentz factor for the wind:
![]() -1000(Goodman 1986; Baring 1995). The second step consists in the
conversion of a fraction of the wind kinetic energy into gamma-rays,
probably via the formation of shocks within the wind itself
(Rees & Mészáros 1994; Daigne & Mochkovitch 1998). Such internal shocks are expected if the
wind is generated with a highly non uniform distribution of the
Lorentz factor so that rapid layers catch up with slower ones. In the
last step, the wind is decelerated when it interacts with the
environment of the source and the resulting external shock is
responsible for the afterglow observed in X-ray, optical and radio
bands.
-1000(Goodman 1986; Baring 1995). The second step consists in the
conversion of a fraction of the wind kinetic energy into gamma-rays,
probably via the formation of shocks within the wind itself
(Rees & Mészáros 1994; Daigne & Mochkovitch 1998). Such internal shocks are expected if the
wind is generated with a highly non uniform distribution of the
Lorentz factor so that rapid layers catch up with slower ones. In the
last step, the wind is decelerated when it interacts with the
environment of the source and the resulting external shock is
responsible for the afterglow observed in X-ray, optical and radio
bands.
The origin of the relativistic wind is the most complex of the three
steps in this scenario. Several proposals have been made but only few
calculations have been performed so that none appears to be fully
conclusive. However it is suspected that large magnetic fields play an
important role. In a previous paper (Spruit et al. 2001) we have
considered different possible geometries of magnetic fields in GRB
outflows and we have proposed that in many cases, dissipation of
magnetic energy by reconnection should occur. The model we have
presented in this paper allows us to investigate these questions in
more details. In particular we focus on the case where the outflow
generated by the central engine is initially Poynting flux dominated
(in the following, we assume that only ![]() of the energy is
initially injected in the matter). To be consistent with the
observations showing that at the beginning of the afterglow emission,
the matter flow is highly relativistic, we also impose that the
terminal Lorentz factor has a large value (in the following, we will
adopt
of the energy is
initially injected in the matter). To be consistent with the
observations showing that at the beginning of the afterglow emission,
the matter flow is highly relativistic, we also impose that the
terminal Lorentz factor has a large value (in the following, we will
adopt
![]() ). This implies a reasonable efficiency of
the magnetic to kinetic energy conversion. The goal of the study
presented in this section is to illustrate that there are geometries
allowing such an efficiency and to discuss the possibility of magnetic
reconnection in this scenario.
). This implies a reasonable efficiency of
the magnetic to kinetic energy conversion. The goal of the study
presented in this section is to illustrate that there are geometries
allowing such an efficiency and to discuss the possibility of magnetic
reconnection in this scenario.
Spruit et al. (2001) have shown that for typical GRB outflows the MHD
approximation is valid to very large distance (
![]()
![]() cm)
which is the main assumption of our calculations. The second main
assumption - the stationarity of the flow - is of course less
justified in the case of GRBs. However we can estimate the time scale
to reach the stationary regime in our wind solutions as the time
needed by a particle starting from the basis of a flow line to reach
the Alfvén point:
cm)
which is the main assumption of our calculations. The second main
assumption - the stationarity of the flow - is of course less
justified in the case of GRBs. However we can estimate the time scale
to reach the stationary regime in our wind solutions as the time
needed by a particle starting from the basis of a flow line to reach
the Alfvén point:
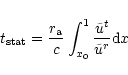 |
(83) |
On the solution we present in Fig. 6, the
acceleration occurs in two phases. First the initial thermal energy is
converted into kinetic energy, the magnetic energy remaining
unchanged. This phase ends at
![]() cm where
cm where
![]() .
The second phase occurs in
the region where the opening angle increases. Here a magnetic to
kinetic energy conversion takes place. We define the acceleration
radius
.
The second phase occurs in
the region where the opening angle increases. Here a magnetic to
kinetic energy conversion takes place. We define the acceleration
radius
![]() as the radius where the flow reaches a Lorentz
factor of
as the radius where the flow reaches a Lorentz
factor of
![]() and the acceleration can be
considered as finished. The value of this radius is completely
dominated by the unknown flow geometry and equals
and the acceleration can be
considered as finished. The value of this radius is completely
dominated by the unknown flow geometry and equals
![]() cm in this case. Even if the location of the
region where the opening angle diverges would extend to higher radii
up to 1010-
cm in this case. Even if the location of the
region where the opening angle diverges would extend to higher radii
up to 1010-![]() cm, this radius is well below two other
important radii: the photosphere radius
cm, this radius is well below two other
important radii: the photosphere radius
![]() where the wind
becomes transparent and the reconnection radius
where the wind
becomes transparent and the reconnection radius
![]() where
the reconnection of the magnetic field should occur. These two radii
have been estimated in Spruit et al. (2001). The photosphere radius is
the solution of
where
the reconnection of the magnetic field should occur. These two radii
have been estimated in Spruit et al. (2001). The photosphere radius is
the solution of
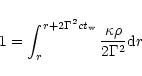 |
(84) |
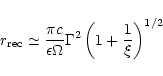 |
(85) |
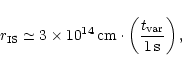 |
(86) |
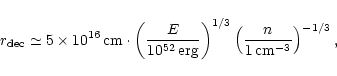 |
(87) |
![\begin{figure}
\par\includegraphics[width=6.5cm,clip]{h2857f6} \end{figure}](/articles/aa/full/2002/03/aah2857/Timg352.gif) |
Figure 6: Geometry, "Lorentz factor'' and energy fluxes for our example. The vertical dotted lines mark the radii of the slow-, the Alfvén-, fast point and the acceleration radius. |
Copyright ESO 2002