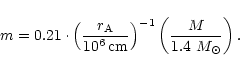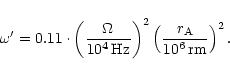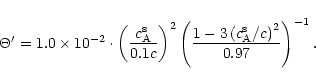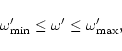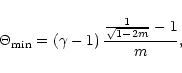Up: Stationary equatorial MHD flows
Subsections
3 Description of the solutions
![\begin{figure}
\par\includegraphics[width=6.8cm,clip]{h2857f1.eps} \end{figure}](/articles/aa/full/2002/03/aah2857/Timg200.gif) |
Figure 1:
Solution plane of the wind equations.
The gray region corresponds to the domain where the Bernoulli
function is well defined. In the sub-Alfvénic region (y>1), it
is limited by the light surface. The thick line (Alfvén mode)
separates the sub- and the super-Alfvénic modes. The dashed
line indicates the slow (y>1) and fast (y<1) mode Mach curves
and the dotted line the gravitational throat curve. The
gravitational throat curve is very close to the fast mode Mach
curve for this particular case. The slow (S) and fast (F)
critical points are the intersections of the Mach and throat
curves. The Alfvén point is indicated by A. |
![\begin{figure}
\par\includegraphics[width=6.8cm,clip]{h2857f2.eps} \end{figure}](/articles/aa/full/2002/03/aah2857/Timg201.gif) |
Figure 2:
A few level contours of the Bernoulli
function are shown. The physical solution (thick line) starts in
the sub-Alfvénic region, crosses the slow mode Mach curve at the
slow critical point (S) then reaches the Alfvén point (A) and
enters the super-Alfvénic region where it crosses the fast mode
Mach curve at the fast critical point (F). This calculation has
been made for a Schwarzschild black hole with m=0.01 and the
parameters (
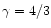 , ,
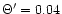 and
and
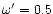 )
have
been chosen so that the different points are well separated. )
have
been chosen so that the different points are well separated. |
As described by Sakurai (1985) in the classical case, the
Bernoulli function
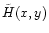 has the following properties:
has the following properties:
- 1.
- At y=1 (
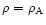 )
)
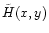 diverges if
diverges if
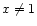 and remains finite if x=1 (
and remains finite if x=1 (
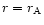 ). It means
that all solutions going from the sub-Alfvénic region (y>1) to
the super-Alfvénic region (y<1) must pass through the Alfvén
point x=y=1 which is the only "hole'' in the infinite "wall''
y=1.
). It means
that all solutions going from the sub-Alfvénic region (y>1) to
the super-Alfvénic region (y<1) must pass through the Alfvén
point x=y=1 which is the only "hole'' in the infinite "wall''
y=1.
- 2.
- Two important curves in the x-y plane are the so called
slow/fast mode Mach curve defined by
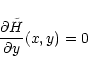 |
(61) |
(the slow mode corresponds to the sub-Alfvénic region y>1 and
the fast mode to the super-Alfvénic region y<1) and the
gravitational throat curve (so called by analogy with the de Laval
nozzle) defined by
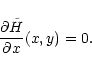 |
(62) |
At the intersections of these two curves, the function
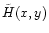 is locally flat, corresponding to an X-type
critical point (or O-type point).
is locally flat, corresponding to an X-type
critical point (or O-type point).
- 3.
- All level contours of
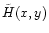 going from
going from
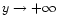 in the sub-Alfvénic region to
in the sub-Alfvénic region to 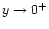 in the super-Alfvénic
region must cross these critical lines. They have to cross
them simultaneously to be not interrupted. This means that the solution
must pass through two critical points defined as the slow
(respectively fast) critical point
in the super-Alfvénic
region must cross these critical lines. They have to cross
them simultaneously to be not interrupted. This means that the solution
must pass through two critical points defined as the slow
(respectively fast) critical point
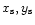 (resp.
(resp.
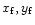 ), intersection of the slow
(resp. fast) mode Mach curve and the gravitational throat curve.
This imposes two new conditions for the solution:
), intersection of the slow
(resp. fast) mode Mach curve and the gravitational throat curve.
This imposes two new conditions for the solution:
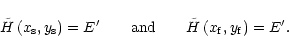 |
(63) |
Figure 1 shows the x-y plane for a particular
choice of the parameters with the slow/fast mode Mach curve, the
gravitational throat curve. Different level contours of the function
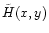 are shown in Fig. 2. The solution is
one of the level contours and passes through the slow and fast
critical points. These figures are very similar to Fig. 1 of
Sakurai (1985) obtained in the classical case. Notice that
Begelman & Li (1994) restrict their study to cold flows. A consequence
of this assumption is that a purely radial flow is a singular case
where the fast critical point is at infinite radius. The fast point
moves inward to finite radii only if the flow diverges over-radially,
like in the situations we will study in the next section. This is not
a necessary condition in our more general model. Because we include
gravity and thermal pressure the fast point is always located at
finite distances even in a purely radial flow.
are shown in Fig. 2. The solution is
one of the level contours and passes through the slow and fast
critical points. These figures are very similar to Fig. 1 of
Sakurai (1985) obtained in the classical case. Notice that
Begelman & Li (1994) restrict their study to cold flows. A consequence
of this assumption is that a purely radial flow is a singular case
where the fast critical point is at infinite radius. The fast point
moves inward to finite radii only if the flow diverges over-radially,
like in the situations we will study in the next section. This is not
a necessary condition in our more general model. Because we include
gravity and thermal pressure the fast point is always located at
finite distances even in a purely radial flow.
![\begin{figure}
\par\includegraphics[width=6.8cm,clip]{h2857f3.eps} \end{figure}](/articles/aa/full/2002/03/aah2857/Timg213.gif) |
Figure 3:
Parameter space: there are no wind solutions in the
lower left part ("Static'': the limits are only approximatively
indicated). The upper left part ("Centrifugal'') corresponds to
winds where the thermal pressure is negligible whereas in the
lower right part ("Thermal'') the centrifugal force plays no
essential role. For a Schwarzschild metric with m=0.01 (so
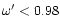 and
and 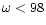 )
we have computed several series of
solutions with constant terminal Lorentz factor )
we have computed several series of
solutions with constant terminal Lorentz factor
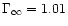 ,
1.5, 10, 100 and 1000 (solid
lines). For ,
1.5, 10, 100 and 1000 (solid
lines). For
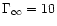 we show also the case where
m=0.1 (dashed line:
we show also the case where
m=0.1 (dashed line: 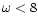 )
and m=0.001 (dotted line: )
and m=0.001 (dotted line:
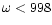 ). The dotted horizontal line corresponds to ). The dotted horizontal line corresponds to 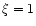 (initially the electromagnetic and the matter energy fluxes are
equal) for m=0.01. For m=0.01 and
(initially the electromagnetic and the matter energy fluxes are
equal) for m=0.01. For m=0.01 and
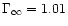 and
1.5 we indicate at different positions the value of the
efficiency
and
1.5 we indicate at different positions the value of the
efficiency
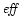 of the magnetic to kinetic energy
conversion.
of the magnetic to kinetic energy
conversion. |
Equation (56) can formally be written as
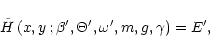 |
(64) |
where m stands for the parameters defining the metric (see
Appendix A for the definition of m in usual cases) and
g stands for the parameters fixing the geometry of the flux tubes
(i.e. defining
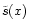 ). We will for the moment restrict our
study to the case where
). We will for the moment restrict our
study to the case where
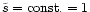 and we fix the
adiabatic index to
and we fix the
adiabatic index to
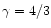 for the rest of this paper. From the
two conditions at the slow/fast critical points (63) we
can fix two parameters. In practice, following Sakurai (1985), we
adjust
for the rest of this paper. From the
two conditions at the slow/fast critical points (63) we
can fix two parameters. In practice, following Sakurai (1985), we
adjust 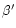 so that the value of
so that the value of 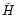 is the same at the
two critical points and this value gives E'. Therefore all solutions
are determined by only three independent parameters:
is the same at the
two critical points and this value gives E'. Therefore all solutions
are determined by only three independent parameters:  ,
,
 and m. Compared to the classical case studied by
Sakurai (1985), there is one supplementary parameter: m. This is
due to the presence of a characteristic length scale related to the
structure of the space-time (typically the gravitational radius
GM/c2) which has no classical counterpart.
and m. Compared to the classical case studied by
Sakurai (1985), there is one supplementary parameter: m. This is
due to the presence of a characteristic length scale related to the
structure of the space-time (typically the gravitational radius
GM/c2) which has no classical counterpart.
The signification of these three parameters is clear: m measures the
intensity of the gravitational field,  gives the strength of
the thermal pressure (the pressureless case which is often considered
corresponds to
gives the strength of
the thermal pressure (the pressureless case which is often considered
corresponds to 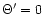 )
and
)
and  measures the strength of the
centrifugal force in accelerating the wind, or equivalently the effect
of the magnetic field.
measures the strength of the
centrifugal force in accelerating the wind, or equivalently the effect
of the magnetic field.
In the limit of the flat space-time (Minkowski metric) it is well
known that the slow point does not exist anymore and that the solution
cannot start at an arbitrary small radius because it cannot cross the
slow mode Mach curve without having an infinite derivative . We
therefore cannot describe the region near the source but this is
clearly because gravity influences the solution significantly at small
radii and the Minkowski approximation breaks down. In the case
without gravity, as in the classical case, a supplementary parameter
(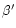 )
must be fixed (for instance by fixing the mass flux). In
many cases the physical conditions at the basis of the wind are a
complex and not well understood question, and some assumptions made
everywhere else in the flow are probably not valid here (like the
adiabaticity). In this context, just adopting a Minkowski metric and
including in the
)
must be fixed (for instance by fixing the mass flux). In
many cases the physical conditions at the basis of the wind are a
complex and not well understood question, and some assumptions made
everywhere else in the flow are probably not valid here (like the
adiabaticity). In this context, just adopting a Minkowski metric and
including in the 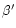 parameter all the unknown physics fixing the
mass flux at the basis of the wind is more elegant than adopting a
Schwarzschild (or Kerr) metric and applying the solution up to the
source.
parameter all the unknown physics fixing the
mass flux at the basis of the wind is more elegant than adopting a
Schwarzschild (or Kerr) metric and applying the solution up to the
source.
Before exploring the three-parameters space we have defined, it is
useful to express the relation between m,  and
and 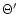 and more usual physical quantities. If m is the ratio of the
gravitational radius of the source over the Alfvén radius, we have
and more usual physical quantities. If m is the ratio of the
gravitational radius of the source over the Alfvén radius, we have
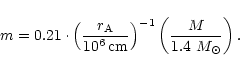 |
(65) |
The angular frequency 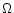 can be identified with the rotation
rate of the source and fixes the value of
can be identified with the rotation
rate of the source and fixes the value of  :
:
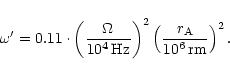 |
(66) |
The local sound speed is defined by
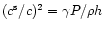 so that
so that 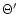 can be related to the ratio of the sound speed at
the Alfvén point
can be related to the ratio of the sound speed at
the Alfvén point
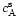 over the speed of light
(for
over the speed of light
(for
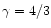 ):
):
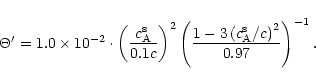 |
(67) |
The three parameters 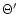 ,
,
 and m being fixed, the
solution of the wind equations is simply found by adjusting
and m being fixed, the
solution of the wind equations is simply found by adjusting 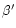 so that the condition (63) is fulfilled. For each step
with
so that the condition (63) is fulfilled. For each step
with 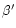 fixed, the slow and fast critical points are determined
by a simple Newton-Raphson procedure. The exact expressions of
fixed, the slow and fast critical points are determined
by a simple Newton-Raphson procedure. The exact expressions of
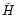 and its derivatives are used. We have explored in detail
the parameter space and the results are presented in
Fig. 3. Notice that for a given m,
and its derivatives are used. We have explored in detail
the parameter space and the results are presented in
Fig. 3. Notice that for a given m,  is
limited to the interval
is
limited to the interval
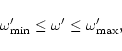 |
(68) |
where
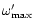 is due to the condition that the Alfvén
point lies inside the light surface and
is due to the condition that the Alfvén
point lies inside the light surface and
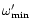 is non
vanishing only in the case of the Kerr metric. In this metric there
are no solutions without rotation (
is non
vanishing only in the case of the Kerr metric. In this metric there
are no solutions without rotation (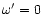 )
because the matter is
forced to rotate in the vicinity of the central source. The analytical
expressions of
)
because the matter is
forced to rotate in the vicinity of the central source. The analytical
expressions of
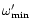 and
and
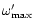 are
given in Appendix A. Here we have considered a
Schwarzschild metric with different values of m. We show the results
in
are
given in Appendix A. Here we have considered a
Schwarzschild metric with different values of m. We show the results
in 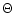 -
-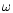 coordinates, where
coordinates, where
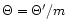 and
and
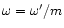 are the parameters used by Sakurai (1985).
Like in the classical case, there are no wind solutions in the lower
left part of the plane ("Static'') because neither the centrifugal
force (magnetic acceleration) nor the thermal pressure are sufficient
to power the wind. The limits of this region are only approximatively
indicated. For a pure thermal wind (
are the parameters used by Sakurai (1985).
Like in the classical case, there are no wind solutions in the lower
left part of the plane ("Static'') because neither the centrifugal
force (magnetic acceleration) nor the thermal pressure are sufficient
to power the wind. The limits of this region are only approximatively
indicated. For a pure thermal wind (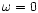 )
and a Schwarzschild
metric, the minimal value of
)
and a Schwarzschild
metric, the minimal value of 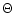 is given by
is given by
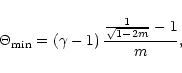 |
(69) |
tending towards 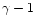 for
for 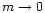 ,
in agreement with the
classical case. In the pressureless case (
,
in agreement with the
classical case. In the pressureless case (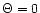 )
the minimal
value of
)
the minimal
value of 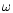 tends towards
(3/2)3/2 for
tends towards
(3/2)3/2 for 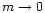 ,
which also
corresponds to the limit given by Sakurai (1985). The upper left
part corresponds to winds where the centrifugal force dominates and
the lower right part corresponds to pure thermal winds. In
Fig. 3 we have plotted several solutions with
constant terminal Lorentz factor
,
which also
corresponds to the limit given by Sakurai (1985). The upper left
part corresponds to winds where the centrifugal force dominates and
the lower right part corresponds to pure thermal winds. In
Fig. 3 we have plotted several solutions with
constant terminal Lorentz factor
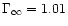 ,
1.5, 10,
100 and 1000 for m=0.01 and in the particular case
,
1.5, 10,
100 and 1000 for m=0.01 and in the particular case
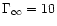 we have also plotted the same curves for m=0.1and m=0.01 to show the effect of varying the gravitational field.
we have also plotted the same curves for m=0.1and m=0.01 to show the effect of varying the gravitational field.


Up: Stationary equatorial MHD flows
Copyright ESO 2002
![]() has the following properties:
has the following properties:
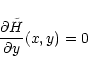
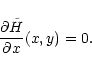
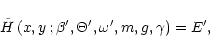
![]() gives the strength of
the thermal pressure (the pressureless case which is often considered
corresponds to
gives the strength of
the thermal pressure (the pressureless case which is often considered
corresponds to ![]() )
and
)
and ![]() measures the strength of the
centrifugal force in accelerating the wind, or equivalently the effect
of the magnetic field.
measures the strength of the
centrifugal force in accelerating the wind, or equivalently the effect
of the magnetic field.
![]() )
must be fixed (for instance by fixing the mass flux). In
many cases the physical conditions at the basis of the wind are a
complex and not well understood question, and some assumptions made
everywhere else in the flow are probably not valid here (like the
adiabaticity). In this context, just adopting a Minkowski metric and
including in the
)
must be fixed (for instance by fixing the mass flux). In
many cases the physical conditions at the basis of the wind are a
complex and not well understood question, and some assumptions made
everywhere else in the flow are probably not valid here (like the
adiabaticity). In this context, just adopting a Minkowski metric and
including in the ![]() parameter all the unknown physics fixing the
mass flux at the basis of the wind is more elegant than adopting a
Schwarzschild (or Kerr) metric and applying the solution up to the
source.
parameter all the unknown physics fixing the
mass flux at the basis of the wind is more elegant than adopting a
Schwarzschild (or Kerr) metric and applying the solution up to the
source.
![]() and
and ![]() and more usual physical quantities. If m is the ratio of the
gravitational radius of the source over the Alfvén radius, we have
and more usual physical quantities. If m is the ratio of the
gravitational radius of the source over the Alfvén radius, we have