

Up: Stationary equatorial MHD flows
Subsections
2 The wind equations
The conservation laws of the general-relativistic magnetohydrodynamics
have been derived by Bekenstein & Oron (1978). Camenzind (1986b)
used these results to obtain the equations governing a stationary
axisymmetric wind. In this section, we first recall these equations
and we apply them to the particular case of a flow occurring in the
equatorial plane. Then we derive a new formulation for this problem
where the wind solution is a level contour of a Bernoulli-like
function. A very similar formulation was earlier studied by
Sakurai (1985) for the non-relativistic case. The similarity
allows us to compare our results with those of the classical case.
Any stationary and axisymmetric space-time can be represented by the
following metric:
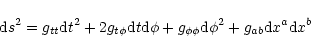 |
(1) |
where the coordinates t and 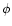 correspond to the two symmetries
of the space-time defined by the two Killing fields
correspond to the two symmetries
of the space-time defined by the two Killing fields
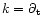 (stationarity) and
(stationarity) and
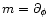 (axisymmetry). The metric coefficients gab depend only on the two
remaining coordinates xa (a=1,2). Note that in the whole paper
we will make use of the (-+++) signature for the metric. The
electromagnetic field is described by the field tensor
(axisymmetry). The metric coefficients gab depend only on the two
remaining coordinates xa (a=1,2). Note that in the whole paper
we will make use of the (-+++) signature for the metric. The
electromagnetic field is described by the field tensor
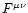 and the dual field tensor
and the dual field tensor
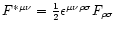 (
(
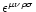 being the Levi-Civita alternating
tensor) which satisfy the Maxwell equations
being the Levi-Civita alternating
tensor) which satisfy the Maxwell equations
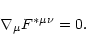 |
(2) |
The motion of the plasma is governed by the energy- and momentum
conservation equation
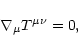 |
(3) |
where the energy-momentum tensor
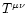 is made up of the fluid
part
is made up of the fluid
part
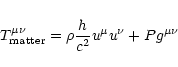 |
(4) |
and of the electromagnetic part
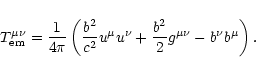 |
(5) |
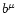 is the magnetic field according to a comoving observer,
written as
is the magnetic field according to a comoving observer,
written as
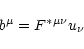 |
(6) |
with
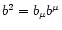 .
In the comoving frame
.
In the comoving frame 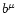 reduces to the
common magnetic field
reduces to the
common magnetic field
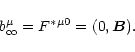 |
(7) |
All dissipative effects (heat conduction, viscosity, cooling by
radiation, etc.) have been neglected so that the flow is adiabatic.
Ideal MHD is also assumed, which means that the proper electric field
as seen in the plasma frame vanishes
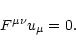 |
(8) |
The following quantities appear in these equations: 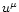 is the
4-velocity,
is the
4-velocity, 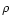 is the comoving mass density, P is the pressure
and h is the specific enthalpy, which is given by (assuming a
constant adiabatic index
is the comoving mass density, P is the pressure
and h is the specific enthalpy, which is given by (assuming a
constant adiabatic index 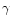 )
)
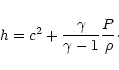 |
(9) |
The last assumption is that the particle number (or mass) is conserved
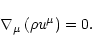 |
(10) |
Before writing the wind equations, it is useful to define the specific
angular momentum of the flow
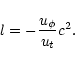 |
(11) |
As a consequence of the symmetries, the non vanishing elements of the
electromagnetic tensor are given by
| Ft1 |
= |
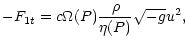 |
(12) |
| Ft2 |
= |
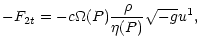 |
(13) |
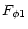 |
= |
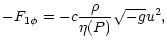 |
(14) |
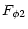 |
= |
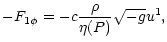 |
(15) |
| F12 |
= |
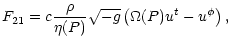 |
(16) |
where the angular frequency of the streamline 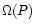 at its
footpoint and the mass flux per unit flux tube
at its
footpoint and the mass flux per unit flux tube 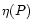 are constant
along each flow line P. The corresponding magnetic field is
are constant
along each flow line P. The corresponding magnetic field is
| bt |
= |
![$\displaystyle \frac{\rho}{\eta(P)} \left[
1+\frac{{u_t u^t}}{{c^2}} \left(
1-\frac{{\Omega(P)l}}{{c^2}}
\right)
\right] ,$](/articles/aa/full/2002/03/aah2857/img88.gif) |
(17) |
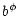 |
= |
![$\displaystyle \frac{\rho}{\eta(P)} \left[
\Omega(P) + \frac{{u_t u}^\phi}{{c^2}} \left(
1-\frac{{\Omega(P) l}}{{c^2}}
\right)
\right],$](/articles/aa/full/2002/03/aah2857/img90.gif) |
(18) |
| b1 |
= |
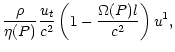 |
(19) |
| b2 |
= |
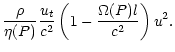 |
(20) |
It is also useful to give the expression of the classical magnetic
field in the frame of the central object for the comparison with the
classical case. In this frame, it is related to the dual field tensor
by
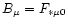 .
Then
.
Then
| Bt |
= |
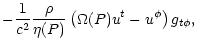 |
(21) |
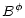 |
= |
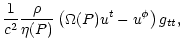 |
(22) |
| B1 |
= |
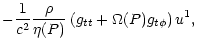 |
(23) |
| B2 |
= |
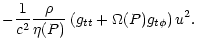 |
(24) |
Because the flow is stationary and axisymmetric, the total angular
momentum L(P) and the total energy
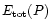 are also
conserved along each flow line P which provides us with two new
equations
are also
conserved along each flow line P which provides us with two new
equations
![$\displaystyle L(P) = -\frac{{u_t}}{{c^2}}\cdot
\biggl\lbrace \frac{{h}}{{c^2}} ...
...^2}} l
+\left( g_{t\phi} + \Omega(P) g_{\phi\phi} \right)
\right]
\biggr\rbrace$](/articles/aa/full/2002/03/aah2857/img100.gif) |
|
|
(25) |
and
![$\displaystyle E_{\rm tot}(P)
= -\frac{{u_t}}{{c^2}}\cdot\biggl\lbrace
h + \Omeg...
...2}} l
+ \left( g_{t\phi} + \Omega(P) g_{\phi\phi}\right)
\right]\biggr\rbrace .$](/articles/aa/full/2002/03/aah2857/img101.gif) |
|
|
(26) |
It is convenient to write the total energy as
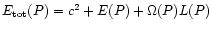 so that the energy conservation can
have the simpler form:
so that the energy conservation can
have the simpler form:
![\begin{displaymath}
E(P) + {c^2} =
-h \frac{{u_t}}{{c^2}}
\left[1-\frac{{\Omega(P)l}}{{c^2}}\right].
\end{displaymath}](/articles/aa/full/2002/03/aah2857/img103.gif) |
(27) |
Each flow line P is completely determined by the four constants
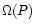 ,
,
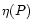 ,
L(P) and E(P). The light surface is
defined by
,
L(P) and E(P). The light surface is
defined by
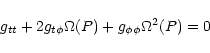 |
(28) |
and the Alfvén point is fixed by two conditions
![\begin{displaymath}\frac{{1}}{{c^2}} \left[
g_{tt} + 2 g_{t\phi}\Omega(P) + g_{\phi\phi}\Omega^2(P)
\right]_{\rm A} =
- M_{\rm A}^2,
\end{displaymath}](/articles/aa/full/2002/03/aah2857/img105.gif) |
(29) |
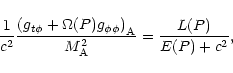 |
(30) |
where the "Mach'' number M is given by
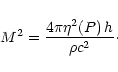 |
(31) |
One sees immediately from (28) and (29) that the
Alfvén point stays always inside the light surface (because of
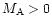 ).
).
We use now the spherical coordinates (x1=r and
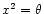 )
and
limit our study to the equatorial plane
)
and
limit our study to the equatorial plane
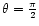 .
The
specification of the flow line P is dropped from here on and
.
The
specification of the flow line P is dropped from here on and
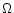 ,
,
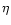 ,
E, and L are used instead of
,
E, and L are used instead of 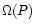 ,
,
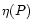 ,
E(P), and L(P). Because of the symmetry,
,
E(P), and L(P). Because of the symmetry, 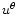 and
and 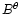 vanish in this plane but this is not necessarily the
case for their derivatives. Then the conservation of mass
(10) can be written
vanish in this plane but this is not necessarily the
case for their derivatives. Then the conservation of mass
(10) can be written
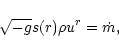 |
(32) |
where the function s(r) depends on the geometry of the flux tubes.
In the simple case where
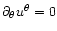 and
and
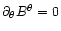 ,
we have
,
we have
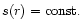 (constant
opening angle). Otherwise we have
(constant
opening angle). Otherwise we have
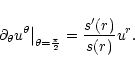 |
(33) |
The conservation of angular momentum (25) and the
conservation of energy (27) read
![$\displaystyle L =
\left[
g_{\phi\phi}\frac{h}{c^2}
- \frac{{g}_{{t}\phi}^{{2}} ...
...}} - {g_{tt} g}_{\phi\phi}}{{c^2}}
\frac{\Phi^2\rho}{4\pi\dot{m}^2}
\right] u^t$](/articles/aa/full/2002/03/aah2857/img120.gif) |
|
|
(34) |
and
E + c2 =![$\displaystyle -h \left[\frac{{g_{tt}} +{\Omega g}_{{t}\phi}}{{c^2}} u^t
+ \frac{{g}_{{t}\phi} + {\Omega g}_{\phi\phi}}{{c^2}} u^\phi
\right],$](/articles/aa/full/2002/03/aah2857/img121.gif) |
(35) |
where instead of using 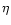 we have introduced the magnetic flux
we have introduced the magnetic flux
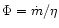 .
The Eqs. (32), (34) and (35)
are completed by the normalization of the four velocity
.
The Eqs. (32), (34) and (35)
are completed by the normalization of the four velocity
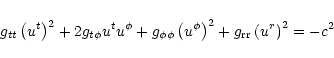 |
(36) |
and the equation of state. We assume here, like in Sakurai (1985),
a polytropic relation
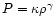 so that the specific
enthalpy is given by
so that the specific
enthalpy is given by
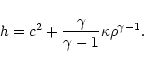 |
(37) |
The system of Eqs. (32), (34)-(37) describes entirely the flow determined by the six
constants
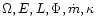 and the free function
s(r). In addition the two supplementary conditions
and the free function
s(r). In addition the two supplementary conditions
and
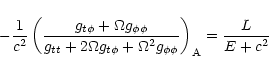 |
(39) |
(all quantities with index A are computed at the Alfvén point) must
be fulfilled, so that the flow remains regular at the Alfvén point.
The classical limit (for a weak gravitational field and for velocities
small compared to the speed of light) of this system of equations in
the case where
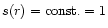 gives exactly the Eqs. (1) to (6) in Sakurai (1985). Notice that E,
gives exactly the Eqs. (1) to (6) in Sakurai (1985). Notice that E, 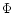 and
and 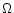 have
the same meaning in both papers whereas we use here different
notations for the mass flux
have
the same meaning in both papers whereas we use here different
notations for the mass flux 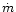 ,
the total angular momentum Land the polytropic constant
,
the total angular momentum Land the polytropic constant 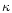 which are respectively f,
which are respectively f,
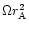 and K in Sakurai (1985). Notice also
that the relation (39) between L and
and K in Sakurai (1985). Notice also
that the relation (39) between L and 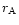 tends
towards
tends
towards
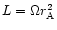 in the classical limit, so that all
notations are fully consistent.
in the classical limit, so that all
notations are fully consistent.
Following Sakurai (1985) we use the dimensionless variables
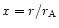 and
and
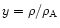 .
The metric
coefficients are also normalized to become dimensionless
.
The metric
coefficients are also normalized to become dimensionless
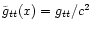 ,
,
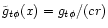 ,
,
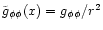 ,
,
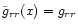 and
and
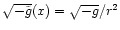 .
These coefficients may be
not only functions of x but also of some parameters defining the
metric (they are given for the Minkowski, Schwarzschild and Kerr
metric in Appendix A). We define
.
These coefficients may be
not only functions of x but also of some parameters defining the
metric (they are given for the Minkowski, Schwarzschild and Kerr
metric in Appendix A). We define
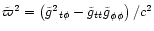 .
We normalize s by
.
We normalize s by
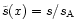 and define a dimensionless specific
enthalpy by
and define a dimensionless specific
enthalpy by
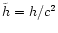 .
Concerning four-vectors like
.
Concerning four-vectors like 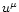 or
or 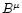 we will use the definitions
we will use the definitions
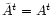 ,
,
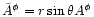 ,
,
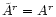 and
and
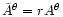 so that the spatial part of these
vectors is now given in the usual basis
so that the spatial part of these
vectors is now given in the usual basis
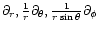 ,
where all components have the same dimension. We introduce four
normalized parameters
,
where all components have the same dimension. We introduce four
normalized parameters
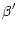 |
= |
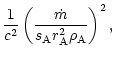 |
(40) |
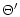 |
= |
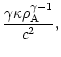 |
(41) |
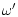 |
= |
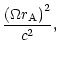 |
(42) |
| E' |
= |
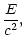 |
(43) |
and we are now able to rewrite the system of Eqs. (32) and
(34) to (37):
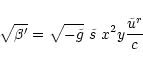 |
(44) |
![$\displaystyle \frac{K_{\rm A}}{M_{\rm A}^2}\left(E'+1\right) =
x\left\lbrace
\l...
...tilde{h}(1)}{M_{\rm A}^2}
\tilde{\varpi}^2 x y\right]
\tilde{u}^t
\right\rbrace$](/articles/aa/full/2002/03/aah2857/img162.gif) |
|
|
(45) |
![$\displaystyle E'+1 =
- \tilde{h}\left[\left(
\tilde g_{tt} + \sqrt{\omega'}\til...
...i} + \sqrt{\omega'}\tilde g_{\phi\phi} x
\right)\frac{\tilde{u}^\phi}{c}\right]$](/articles/aa/full/2002/03/aah2857/img163.gif) |
|
|
(46) |
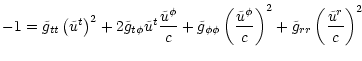 |
|
|
(47) |
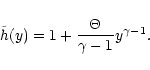 |
(48) |
In (46) and (45) the constants
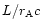 and
and
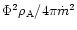 have been eliminated using the
conditions (38) and (39) at the Alfvén point, which
now read
have been eliminated using the
conditions (38) and (39) at the Alfvén point, which
now read
and
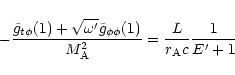 |
(50) |
so that
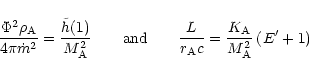 |
(51) |
with
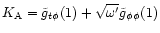 .
.
The component
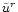 can be expressed from (44) and
substituted into (47) to provide a first relation between
can be expressed from (44) and
substituted into (47) to provide a first relation between
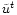 and
and
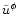 .
A second relation between these
two components is given by (45) when subtracting
.
A second relation between these
two components is given by (45) when subtracting
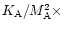 (46). It allows us to
express all components of the four velocity as functions of only xand y. Then the remaining Eq. (46) becomes a Bernoulli-like
equation
(46). It allows us to
express all components of the four velocity as functions of only xand y. Then the remaining Eq. (46) becomes a Bernoulli-like
equation
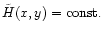 as (10) of
Sakurai (1985). We do not further elaborate on the different
steps which lead to this final expressions:
as (10) of
Sakurai (1985). We do not further elaborate on the different
steps which lead to this final expressions:
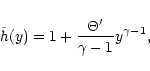 |
(52) |
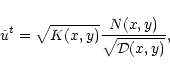 |
(53) |
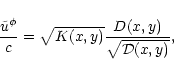 |
(54) |
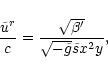 |
(55) |
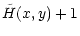 |
= |
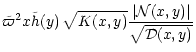 |
|
| |
= |
E'+1, |
(56) |
where we have introduced the following auxiliary functions:
| K(x,y) |
= |
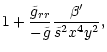 |
(57) |
| N(x,y) |
= |
![$\displaystyle \left[
\left(M_{\rm A}^2+\sqrt{\omega'}K_{\rm A}\right)
\tilde g_...
...\rm A} \tilde g_{t\phi}
\right] \tilde{h}(y)
-\tilde{h}(1)\tilde{\varpi}^2 x y,$](/articles/aa/full/2002/03/aah2857/img185jal.gif) |
(58) |
| D(x,y) |
= |
![$\displaystyle -\left[
\left(M_{\rm A}^2+\sqrt{\omega'}K_{\rm A}\right)
\tilde g...
... g_{tt}
\right] \tilde{h}(y)
-\sqrt{\omega'}\tilde{h}(1)\tilde{\varpi}^2 x^2 y,$](/articles/aa/full/2002/03/aah2857/img186jal.gif) |
|
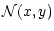 |
= |
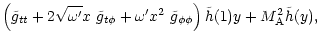 |
(59) |
 |
= |
![$\displaystyle -\left[
\tilde g_{\phi\phi} D^2(x,y) + 2\tilde g_{t\phi} D(x,y) N(x,y)
+\tilde g_{tt} N^2(x,y)\right].$](/articles/aa/full/2002/03/aah2857/img190jal.gif) |
(60) |
Equation (56) is the Bernoulli equation we will now
consider. The solution y(x) of the wind equations appears as the
level contour E' of the surface H(x,y). Notice that the classical
limits of 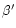 ,
,
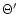 and
and  are not exactly the
corresponding
are not exactly the
corresponding 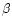 ,
,
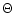 and
and 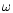 parameters used by
Sakurai (1985), who made the choice of normalizing
these quantities with the value of the gravitational potential at the
Alfvén point
parameters used by
Sakurai (1985), who made the choice of normalizing
these quantities with the value of the gravitational potential at the
Alfvén point
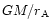 (see Eqs. (11a), (11b) and (11c) of
Sakurai 1985) whereas we used c2 to make the definition of
these parameters more general. However a simple relation applies
between Sakurai's and our parameters:
(see Eqs. (11a), (11b) and (11c) of
Sakurai 1985) whereas we used c2 to make the definition of
these parameters more general. However a simple relation applies
between Sakurai's and our parameters:
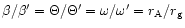 where
where
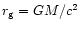 is the gravitational radius. This is also valid
for the classical limit of the Bernoulli function
is the gravitational radius. This is also valid
for the classical limit of the Bernoulli function
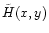 and the definition used by Sakurai (1985).
and the definition used by Sakurai (1985).
Before studying
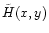 in the following section, we have to
note that this function is not defined everywhere in the region x>0,
y>0 as it is the case in the classical limit. The function
in the following section, we have to
note that this function is not defined everywhere in the region x>0,
y>0 as it is the case in the classical limit. The function
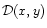 must be strictly positive so that
must be strictly positive so that
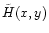 is well defined and the velocities are not imaginary. The domain
where this condition applies is determined in
Appendix C. In the sub-Alfvénic region (y>1) this
domain lies always inside the light surface, its location is given
more precisely in Appendix B.
is well defined and the velocities are not imaginary. The domain
where this condition applies is determined in
Appendix C. In the sub-Alfvénic region (y>1) this
domain lies always inside the light surface, its location is given
more precisely in Appendix B.


Up: Stationary equatorial MHD flows
Copyright ESO 2002
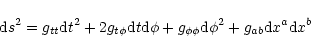
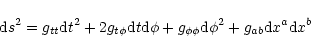
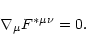
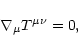
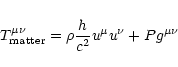
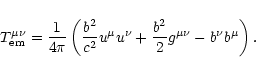
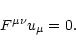
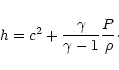
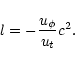
![$\displaystyle \frac{\rho}{\eta(P)} \left[
1+\frac{{u_t u^t}}{{c^2}} \left(
1-\frac{{\Omega(P)l}}{{c^2}}
\right)
\right] ,$](/articles/aa/full/2002/03/aah2857/img88.gif)
![$\displaystyle \frac{\rho}{\eta(P)} \left[
\Omega(P) + \frac{{u_t u}^\phi}{{c^2}} \left(
1-\frac{{\Omega(P) l}}{{c^2}}
\right)
\right],$](/articles/aa/full/2002/03/aah2857/img90.gif)
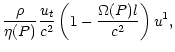
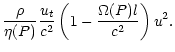
![$\displaystyle E_{\rm tot}(P)
= -\frac{{u_t}}{{c^2}}\cdot\biggl\lbrace
h + \Omeg...
...2}} l
+ \left( g_{t\phi} + \Omega(P) g_{\phi\phi}\right)
\right]\biggr\rbrace .$](/articles/aa/full/2002/03/aah2857/img101.gif)
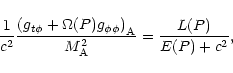
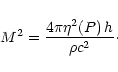
![]() )
and
limit our study to the equatorial plane
)
and
limit our study to the equatorial plane
![]() .
The
specification of the flow line P is dropped from here on and
.
The
specification of the flow line P is dropped from here on and
![]() ,
,
![]() ,
E, and L are used instead of
,
E, and L are used instead of ![]() ,
,
![]() ,
E(P), and L(P). Because of the symmetry,
,
E(P), and L(P). Because of the symmetry, ![]() and
and ![]() vanish in this plane but this is not necessarily the
case for their derivatives. Then the conservation of mass
(10) can be written
vanish in this plane but this is not necessarily the
case for their derivatives. Then the conservation of mass
(10) can be written
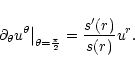
![]() gives exactly the Eqs. (1) to (6) in Sakurai (1985). Notice that E,
gives exactly the Eqs. (1) to (6) in Sakurai (1985). Notice that E, ![]() and
and ![]() have
the same meaning in both papers whereas we use here different
notations for the mass flux
have
the same meaning in both papers whereas we use here different
notations for the mass flux ![]() ,
the total angular momentum Land the polytropic constant
,
the total angular momentum Land the polytropic constant ![]() which are respectively f,
which are respectively f,
![]() and K in Sakurai (1985). Notice also
that the relation (39) between L and
and K in Sakurai (1985). Notice also
that the relation (39) between L and ![]() tends
towards
tends
towards
![]() in the classical limit, so that all
notations are fully consistent.
in the classical limit, so that all
notations are fully consistent.
![]() and
and
![]() .
The metric
coefficients are also normalized to become dimensionless
.
The metric
coefficients are also normalized to become dimensionless
![]() ,
,
![]() ,
,
![]() ,
,
![]() and
and
![]() .
These coefficients may be
not only functions of x but also of some parameters defining the
metric (they are given for the Minkowski, Schwarzschild and Kerr
metric in Appendix A). We define
.
These coefficients may be
not only functions of x but also of some parameters defining the
metric (they are given for the Minkowski, Schwarzschild and Kerr
metric in Appendix A). We define
![]() .
We normalize s by
.
We normalize s by
![]() and define a dimensionless specific
enthalpy by
and define a dimensionless specific
enthalpy by
![]() .
Concerning four-vectors like
.
Concerning four-vectors like ![]() or
or ![]() we will use the definitions
we will use the definitions
![]() ,
,
![]() ,
,
![]() and
and
![]() so that the spatial part of these
vectors is now given in the usual basis
so that the spatial part of these
vectors is now given in the usual basis
![]() ,
where all components have the same dimension. We introduce four
normalized parameters
,
where all components have the same dimension. We introduce four
normalized parameters
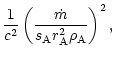
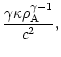
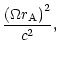
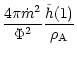
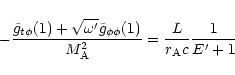
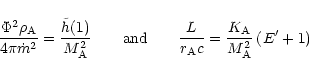
![]() can be expressed from (44) and
substituted into (47) to provide a first relation between
can be expressed from (44) and
substituted into (47) to provide a first relation between
![]() and
and
![]() .
A second relation between these
two components is given by (45) when subtracting
.
A second relation between these
two components is given by (45) when subtracting
![]() (46). It allows us to
express all components of the four velocity as functions of only xand y. Then the remaining Eq. (46) becomes a Bernoulli-like
equation
(46). It allows us to
express all components of the four velocity as functions of only xand y. Then the remaining Eq. (46) becomes a Bernoulli-like
equation
![]() as (10) of
Sakurai (1985). We do not further elaborate on the different
steps which lead to this final expressions:
as (10) of
Sakurai (1985). We do not further elaborate on the different
steps which lead to this final expressions:
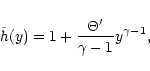
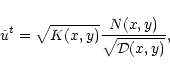
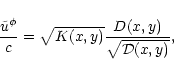
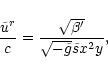
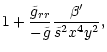
![]() in the following section, we have to
note that this function is not defined everywhere in the region x>0,
y>0 as it is the case in the classical limit. The function
in the following section, we have to
note that this function is not defined everywhere in the region x>0,
y>0 as it is the case in the classical limit. The function
![]() must be strictly positive so that
must be strictly positive so that
![]() is well defined and the velocities are not imaginary. The domain
where this condition applies is determined in
Appendix C. In the sub-Alfvénic region (y>1) this
domain lies always inside the light surface, its location is given
more precisely in Appendix B.
is well defined and the velocities are not imaginary. The domain
where this condition applies is determined in
Appendix C. In the sub-Alfvénic region (y>1) this
domain lies always inside the light surface, its location is given
more precisely in Appendix B.