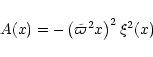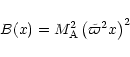![\begin{figure}
\par\mbox{\includegraphics[width=8.6cm]{h2857fa1}\hspace*{2mm}
\...
...m]{h2857fa2} }
\mbox{\includegraphics[width=8.8cm]{h2857fa3} }
\end{figure}](/articles/aa/full/2002/03/aah2857/Timg368.gif) |
Figure C.1:
Domain of definition of the
Bernoulli function: we consider a Schwarzschild black hole
and draw this domain for different values of m and  (variations of
(variations of 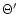 correspond only to a contraction or a
dilatation of the domain along the y axis. We adopt here
correspond only to a contraction or a
dilatation of the domain along the y axis. We adopt here
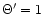 ). Cases a) and b):
m=0.2<m*. There are
three possible configurations depending on the value of ). Cases a) and b):
m=0.2<m*. There are
three possible configurations depending on the value of
 .
Case a) corresponds to .
Case a) corresponds to
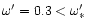 and
case b to
and
case b to
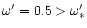 .
The case .
The case
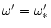 looks very similar to case b) and is not plotted. We added the
fast/slow mode Mach curves (dotted line) and the gravitational
throat curve (dashed line) with the corresponding slow (S) and
fast (F) critical point. The thick line is the solution passing
through S, F and the Alfvén point A. Case c)
m=m*=1/3. This is the critical case where it is still
possible to find a solution (here
looks very similar to case b) and is not plotted. We added the
fast/slow mode Mach curves (dotted line) and the gravitational
throat curve (dashed line) with the corresponding slow (S) and
fast (F) critical point. The thick line is the solution passing
through S, F and the Alfvén point A. Case c)
m=m*=1/3. This is the critical case where it is still
possible to find a solution (here
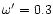 and
and
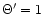 ). ). |