3 Propagation, slow-down and capture of neutrons in the atmosphere of the secondary

A fraction of the neutron flux emitted by the accretion disk irradiates the atmosphere of the secondary star. Some of these neutrons get thermalized; some are captured by nuclei, others decay or escape the secondary if after several scatterings their kinetic energies become larger than the gravitational potential energy binding them to the star. The 2.22 MeV photons resulting from the capture of neutrons by protons escape the secondary atmosphere if they are not absorbed or Compton scattered in the surrounding gas. Consequently, the probability of escape of 2.22 MeV photons depends on the depth of their creation site (in the atmosphere) and on their direction of emission with respect to the surface.

These processes have all been modeled, in the aim of determining the rate of 2.22 MeV radiation emitted by the secondary. The transport of neutrons in the secondary has been simulated using the code GEANT/GCALOR, which takes into account elastic and inelastic interactions as well as the neutrons' decay and capture by nuclei. The radiative transfer of 2.22 MeV photons in the atmosphere and the fraction of neutrons falling back onto the secondary are then modeled separately, using the results of the previous simulations. The total emissivity at 2.22 MeV is estimated by integrating over the whole secondary surface irradiated by neutrons. In the following paragraphs details of the method are presented.

The secondary star has a mass and a radius denoted hereafter by $M_{\rm s}$ and $R_{\rm s}$. (There should be no confusion between the Schwarzchild radius ($R_{\rm S}$) of the primary and the radius ($R_{\rm s}$) of the secondary star.) The star's atmosphere is characterized by a temperature $T_{\rm s}$, a density $\rho_{\rm s}$ and an abundance in H and in He of [H] and [He], respectively. The isotopic abundance of these elements are taken from Anders & Grevesse (1989). We have disregarded all other elements in the atmosphere. The distance between the accretion disk and the center of the secondary (also called separation) is parametrized by $d_{\rm s}$. This distance $d_{\rm s}$ and the radius of the star determine the fraction of the neutron flux emitted by the accretion disk that irradiates the secondary. The secondary's mass and radius allow us to calculate the gravitational potential and therefore the fraction of escaping neutrons, which also depends on their energy and direction. The temperature, the density, and the composition of the atmosphere are parameters for the simulation of neutron tracks in the secondary. The abundance of ³He is a crucial parameter for the intensity of the 2.22 MeV line emission since, though it is estimated to be $\approx$10⁵ less abundant than H, it has a cross section for neutron capture $1.61 \times 10^4$ times that of H. Consequently, this isotope is able to remove neutrons from the atmosphere rather efficiently, thereby reducing the rate of their capture by protons. The density and the composition also determine the mean free path of 2.22 MeV photons in the atmosphere.

Simulations of neutrons with an energy $E_{\rm n}$ impinging on the atmosphere at a zenith angle $\psi$ have also been performed. For each assumption of $E_{\rm n}$ and $\psi$, a depth distribution of neutron capture by H ( ${\rm d}f_{\rm d}(z;E_{\rm n},\psi)/{\rm d}z$) and an energy and zenithal distribution of neutrons leaving the atmosphere ( ${\rm d}F(E,\theta;E_{\rm n},\psi) /({\rm d}E {\rm d}\theta)$) are computed. These distributions are normalized to the number of impinging neutrons. Figure 2 shows the depth distribution of the sites of neutron capture by protons for neutrons impinging with an angle of 40 degrees. For neutron energies lower than $\approx$0.01 MeV, the depth distribution of neutron capture sites and the energy and zenithal distribution of neutrons leaving the atmosphere are rather constant (with respect to energy) for a given initial zenith angle. In fact, at these energies, the neutrons are quickly thermalized in the vicinity of the surface and all follow the same thermal diffusion.

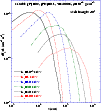Figure 2: Distributions of the neutron capture sites in the secondary's atmosphere for several impinging neutron energies.

Depending on their energy and direction, some of the neutrons that are ejected out of the atmosphere get decelerated gravitationally and fall back onto the secondary's surface; some of them decay in the process. This fraction ( $F_{\rm r}(E_{\rm n},\psi)$) of neutrons returning to the atmosphere depends on the energy and zenith angle of the impinging neutrons. Indeed, the larger the neutrons' energy, the deeper they can go, and the smaller the zenith angle of the impinging neutrons the deeper they will also go. Consequently, the probability for a neutron to leave the atmosphere decreases with increasing energy and decreasing zenith angle. The fraction $F_{\rm r}(E_{\rm n},\psi)$ is calculated using Eq. (19) of Hua & Lingenfelter (1987), which determines the time required for a neutron to return to the atmosphere as a function of its energy and zenith angle. This time is used to determine the fraction of neutrons decaying in flight before they return to the atmosphere. The spectrum of the escaping and returning neutrons has a cut-off value below the escape energy ( $E_{\rm n}^{({\rm esc})} = {GMm_{\rm n} \over R} \approx 2\ {\rm keV} {{M/M_{\odot}} \over {R/R_{\odot}}}$) because even if a neutron has a kinetic energy a little less than the escaping energy, the time spent to return to the atmosphere can be larger than its lifetime.

The angular distribution of the returning neutrons is very close to an isotropic distribution. Simulations have thus been performed to derive the depth distribution of 2.22 MeV creation sites ( ${\rm d}f_r(z)/{\rm d}z$) due to returning neutrons. As previously stated, this distribution is flat for low neutron energies. A fraction $F_{\rm r,0}$ of these returning neutrons can again leave the secondary. However they all return to the atmosphere, since their energies are smaller than the escaping energy, and they can then again undergo one of the following: generate 2.22 MeV photons, decay, be captured by ³He, or leave again the secondary atmosphere (with a fraction given by $F_{\rm r,0}$).

The total depth distribution for the radiative capture of neutrons is obtained by adding to the "direct" depth distribution (without taking into account the returning neutrons) the returning-neutrons component. This component is obtained by calculating the sum of the geometric series of the fraction $F_{\rm r,0}$. The total depth distribution of 2.22 MeV creation site is then:

$$\frac{{\rm d}f(z;E_{\rm n},\psi)}{{\rm d}z} = \frac{{\rm d}f_... ...rm d}z} \frac{F_{\rm r}(E_{\rm n},\psi)}{(1-F_{\rm r,0})}\cdot$$ (12)

The angular distribution of the escaping 2.22 MeV photons is computed using the total depth distribution of 2.22 MeV photon creation sites. Let $\xi$ and $\chi$ be the zenithal and azimutal direction angles of the 2.22 MeV photon. The angular distribution of escaping 2.22 MeV photons induced by a neutron of energy $E_{\rm n}$ impinging on the atmosphere with a zenith angle of $\psi$ is:

$$\frac{{\rm d}\epsilon_{2.2}(\xi,\chi;E_{\rm n},\psi)}{{\rm d}... ... d}z} \, {\rm e}^{\frac{-z}{\lambda_{2.2}\cos\xi}} \, {\rm d}z$$ (13)

with $\lambda_{2.2}$ being the mean free path of 2.22 MeV photons in the secondary's atmosphere. This angular distribution, expressed in photons steradian^-1 neutron^-1, is independent of the azimuth. Figure 3 shows an example of 2.22 MeV photons angular distribution for neutrons impinging with various $E_{\rm n}$'s at a zenith angle of 0$^{\rm o}$.

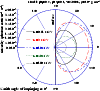Figure 3: Angular distributions of the 2.22 MeV photons emitted from the secondary atmosphere for several impinging neutron energies.

The total 2.22 MeV intensity depends on the direction of observation with respect to the binary system frame. Indeed, the 2.22 MeV photons are emitted only from the surface of the secondary that is irradiated by neutrons. Therefore, the observable gamma-ray flux comes only from the fraction of the secondary area that is irradiated by neutrons and is visible for the observer (see Fig. 4). So we can expect to observe a periodic 2.2 MeV line flux due to the rotation of the binary system. The total 2.22 MeV intensity $I_{2.2}(\alpha,\delta)$ (photons s^-1sr^-1) in a direction ($\alpha$, $\delta$) can be obtained by estimating the integral:

$$I_{2.2}(\alpha,\delta) = \frac{N_{\rm n}}{4\pi} \int_{D} \int... ..._{2.2}(\xi,\chi;E,\psi)}{{\rm d}\Omega} {\rm d}\Omega {\rm d}E$$ (14)

where ${\rm d}F(E)/{\rm d}E$ is the energy distribution of neutrons reaching the secondary, $N_{\rm n}$ is the neutron rate (in n s^-1) emitted by the accretion disk, $\varphi$ and $\theta$ the direction of the emitted neutrons (see Fig. 4) and D is the integration domain ( $\varphi , \theta \in D$) defined as the intersection of the irradiated area (delimited in a cone of angle $\varphi_{\rm max}$) and the visible area in the direction $\alpha$ and $\delta$. In this equation, $\xi$ is a function of $\varphi$, $\theta$, $\alpha$ and $\delta$. The zenith angle $\psi$ depends only on $\varphi$. The integration domain depends not only on the direction of emission but also on the radius of the secondary and on its distance with respect to the neutron source.

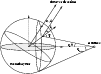Figure 4: Schematic view of the irradiation of the secondary star by neutrons. The binary system frame is represented by the dashed axes.