4 Results

We have considered two models for the composition and the geometrical characteristics of the secondary star (see Table 6). The values shown in the table have been chosen so as to compare neutron capture efficiency in helium-enriched and non-enriched ("normal'') atmospheres. Calculations of the 2.22 MeV emissivity with specific, accurate secondary star parameters of known binary systems will be presented in a separate publication (Jean et al. 2001, in preparation).

  

Table 6: Characteristics of the secondary star for the two models.

Calculations based on the method presented in the previous section have been performed in the aim of deriving the expected flux in the 2.22 MeV line from the binary system. The energy distribution of neutrons was assumed to be a Maxwellian with kT = 10 MeV, truncated at 5 MeV ($E_{\rm c}$ in Eq. (14)) because the gravitationnal potential of the primary compact object retains the neutrons of lower energy (see Sect. 2). Since we are dealing with close binary systems, the separation is less than 40 $R_{\odot }$, which is the mean free path of 5 MeV neutrons in the vacuum. Therefore, the energy distribution does not necessitate an additionnal cut to account for the loss of neutrons by decay during their trip to the secondary star.

  
4.1 Fraction of escaping 2.22 MeV photons

The fraction of escaping 2.22 MeV radiation (f_2.2) is defined as the ratio of 2.22 MeV photons that reach the secondary star surface (outward) without scattering to the total number of incident neutrons. This fraction is calculated by integrating the angular distribution of escaping 2.22 MeV photons (see Eq. (4)) over all the possible angles. The 2.22 MeV photons produced by the returning neutrons are also taken into account. The fraction f_2.2 depends on the zenith angles and energies of incident neutrons. It gives an idea of the efficiency of neutrons in producing an observable 2.22 MeV line. Figures 5 show the escaping 2.22 MeV fraction for the two models of the secondary star. The difference in the neutron capture rate between the two models is principally due to the difference in the composition of the atmosphere. Indeed the abundance of ³He in the second model is such that a large fraction of neutrons are captured by this nucleus and thus lost. Consequently, the neutrons capture rate decreases by a factor $\approx$17 between the two models. In Model-2 the 2.22 MeV photons are emitted deeper in the atmosphere, and so their shorter mean free path lowers the fraction of escaping photons by a factor 1.5 compared to Model-1. Finally, the gravitational escaping energy of neutrons in Model-2 is slighty lower than in Model-1, increasing the fraction of escaping neutrons and further reducing the 2.22 MeV emissivity in Model-2. All these effects lead to a decrease of f_2.2 by a factor $\approx$30 for Model-2 with respect to Model-1 at low $E_{\rm n}$.

The fraction of escaping 2.22 MeV photons depends not only on the neutron capture rate but also on the transmission of 2.22 MeV photons in the atmosphere. In Model-1 (see Fig. 5a), where the neutron energy is lower than the escaping energy, the neutrons thermalize quickly and stay in the upper layer of the atmosphere. If they leave the atmosphere, they cannot escape the secondary but a fraction of them decay before returning in the atmosphere. The fraction of escaping neutrons increases with the zenith angle. Indeed, high-zenith-angle incident neutrons can more easily escape since they scatter close to the surface. This is not the case for low-zenith-angle incident neutrons that go deeper in the atmosphere: even if they scatter toward the surface, their energies are rarely above the escape value. This explains why the f_2.2 fraction decreases with increasing zenith angle below 5 MeV. Above 5 MeV, neutrons penetrate and are captured deeper in the atmosphere. The fraction of escaping neutrons is reduced, as well as the transmission of 2.22 MeV photons. However, for large zenith angles, the neutron captures happen closer to the surface in zones allowing the 2.22 MeV photons to escape more easily from the star.

The variation of the 2.22 MeV photon escaping fraction as a function of the angle and the energy of impinging neutrons in Model-2 is similar to that in Model-1. However, a resonance in the elastic scattering of neutrons with ⁴He at 1.1 MeV is at the origin of the drop around 1 MeV (see Fig. 5b). At this resonance, the angular distribution of ⁴He-scattered neutrons is peaked for backward directions. Consequently, around 1 MeV, incident neutrons are more likely to backscatter and to be ejected out of the atmosphere with kinetic energies too high to allow them to return. This effect reduces the number of MeV neutrons that can thermalize and produce 2.2 MeV photons, hence the trough seen in Fig. 5b.

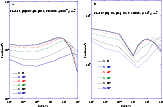Figure 5: Fraction of escaping 2.2 MeV photons as a function of the impinging neutron energies for several impinging zenith angle. The two models are presented separately.

  
4.2 Flux versus model and irradiation geometry

The distance between the accretion disk (the source of neutrons) and the center of the secondary star, and the angles $\alpha$ and $\delta$, which specify the direction of Earth (see Fig. 4), are the basic parameters of this calculation. Since the binary system is rotating, $\alpha$ varies with time and the observed flux becomes periodic. Intensities have been calculated as a function of the direction of emission for different values of the distance between the primary and secondary stars. Assuming parameters of the binary system (separation and masses), it has been possible to derive light curves of the 2.22 MeV line emission, depending on $\delta$. However, the range of interesting separations is limited since the secondary radius needs to fill its Roche lobe in order to allow the accretion of its matter by the compact object. Using a study by Paczynski (1971) that calculated the critical radius of a star in a binary system that allows the outward flow of its matter, we estimated the upper limit of the separation to be between 3.5-6 $R_{\odot }$ for a secondary star of 1 $M_{\odot }$ (Model-1) and 7.5-11 $R_{\odot }$ for a secondary star of 10 $M_{\odot }$ (Model-2), providing compact object masses ranging from 3 to 20 $M_{\odot }$. With this type of close binary systems, the period of rotation is less than a day.

Figure 6 shows phasograms of the 2.22 MeV intensity as a function of the separation for Model-1. As expected, the intensity is maximum when the neutron-irradiated area of the secondary star atmosphere faces the observer. The maximum value of the intensity decreases with increasing separation values because the neutrons flux impinging on the atmosphere decreases with increasing distance between the accretion disk and the secondary. In Fig. 6, the intensity is equal to zero at a phase value of 0.5 only for a separation of 1.5 $R_{\odot }$, because for this value of $\delta$ the irradiated area is hidden by the star. For larger separations, the irradiated area becomes larger and a fraction of this area is always visible by the observer.

Figure 6: Example of phasogram of the 2.2 MeV emission for the Model-1 with a compact object mass of 3 $M_{\odot }$. $\delta$ is the angle between the binary system plan and the direction of the observer. D is the distance between the accretion disk and the secondary star in solar radius unit. The period of the binary system change from 0.1 to 0.4 days.

The mean and the root-mean-square (rms) fluxes are commonly used for the analysis of periodic emissions. They have been estimated for our 2.22 MeV intensity as a function of the separation and the direction of the observer. Both the mean and the rms intensities decrease with increasing separation values as a power law with slope around -2 (between -1.8 and -2.3). Figures 7 and 8 show the variation of the mean and rms intensities as a function of the binary separation for the two models.

  

Table 7: Mean 2.22 MeV flux vs. accretion disk models (at 1 kpc for a separation of 2 $R_{\odot }$ and an initial 90% H and 10% He composition).

The mean intensity does not vary significantly with the angle of the Observer's direction with respect to the binary system plane. The rms intensity decreases, however, showing a reduction of the modulation of the visible photon flux with increasing $\delta$. The modulation obviously disappears for a direction of observation of the binary system perpendicular to the plane of the latter ( $\delta=90^{\rm o}$).

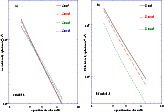Figure 7: Normalized mean a) and rms b) intensities for Model-1 as a function of the separation of the binary. Several values of $\delta$ are shown.

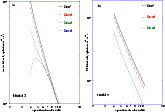Figure 8: Normalized mean a) and rms b) intensities for Model-2 as a function of the separation of the binary. Several values of $\delta$ are shown.

The flux at 2.22 MeV can be derived using the formula:

$$F_{2.2} = 10^{-5} \, \frac{R_{\rm n}}{10^{40} \, {\rm n} \, {... ...sr}^{-1}} \, d^{-2}_{\rm kpc} \, {\rm s}^{-1} \, {\rm cm}^{-2}$$ (15)

where $R_{\rm n}$ is the rate of neutrons emitted by the accretion disk, I_2.2 is the normalized intensity and $d_{\rm kpc}$ the distance of the binary system to the observer in kpc. For Model-1, the flux at 1 kpc is found to be in the range 10^-7-10^-5 photons s^-1 cm^-2depending on the accretion disk model. For Model-2, it is found to be in the range 10^-8 to 10^-6 photons s^-1 cm^-2depending on the accretion disk model. Combining the results of $R_{\rm n}$ from Sect. 2 (Tables 1a, b to 5a, b) with the calculations in this section, we obtain the final fluxes F_2.2, which we present succinctly in Tables 7 and 8. The separations have been chosen to be 2 $R_{\odot }$ and 8 $R_{\odot }$for Model-1 and Model-2 respectively, since for these values the mean fluxes do not change significantly with the binary system inclination (see Figs. 7 and 8).

  

Table 8: Mean 2.22 MeV flux vs. accretion disk models (at 1 kpc for a separation of 8 $R_{\odot }$ and an initial 10% H and 90% He composition).

The rotation of the binary system leads to a shift in the centroid of the 2.22 MeV line. This Doppler shift changes with the phase and depends on the observer's direction ($\delta$). Using classical relations in binary systems (e.g. Franck et al. 1992) we derive a relation (Eq. (16)) for the spectral shift of the 2.22 MeV line which depends on the masses of the compact object and the secondary ($M_{\rm c}$ and $M_{\rm s}$, respectively, in solar masses), the separation between the two objects ($d_{\rm s}$ in solar radii), the phase ($\phi$), and the angle between the observer's direction and the binary system ($\delta$).

$$\Delta E = 3.2 \, \frac{M_{\rm c}}{\sqrt{d_{\rm s}(M_{\rm c}+M_{\rm s})}} \, \cos\delta \, \sin\phi \; {\rm keV}.$$ (16)

The estimated spectral shift is mesurable with SPI, the spectrometer onboard the INTEGRAL satellite. Using Eq. (16) and the intensity variation as a function of the phase (as presented in Fig. 6) we have obtained the 2.22 MeV line profiles for Model-1 (Figs. 9) with a compact companion of 3 $M_{\odot }$ and for two values of the binary system
inclination. The line is broadened and double-peaked due to the rotation of the secondary star. Figures 10 show the shape of the line as it could be measured by SPI (assuming a spectral resolution of 2.9 keV at 2.22 MeV). For an inclination of 80$^{\rm o}$ the double-peak shape is clearly visible, whereas for a 10$^{\rm o}$ inclination that is not the case.

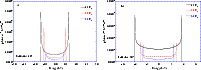Figure 9: Shape of the neutron capture line for Model-1. The inclination of the binary system is 10$^{\rm o}$ a) and 80$^{\rm o}$ b). Several values of the binary separation are shown.

Figure 10: Estimation of the neutron capture line shape for Model-1 as it could be measured by the spectrometer SPI of INTEGRAL. The inclination of the binary system is 10$^{\rm o}$ a) and 80$^{\rm o}$ b). Several values of the binary separation are shown.