2 Neutron production in the accretion disk

Neutrons are produced by means of nuclear breakup reactions involving hydrogen and helium nuclei. Once produced, the neutrons can escape or carry part of the angular momentum outward by collisions with the infalling nuclei, thereby participating in the viscous dissipation, as they are not affected by the presence of any magnetic fields. In fact, the escape of the neutrons from the gravitational attraction of the compact object can be computed quite accurately in the assumption of thermal conditions (Aharonian & Sunyaev 1984; Guessoum & Kazanas 1990). So, at least in principle, the calculation of the flux of neutrons irradiating the surface of the companion star is quite feasible. In practice, however, there are a number of factors which intervene and make the task somewhat more complicated: the temperature and density distribution of matter in the accretion disk is model-dependent, the composition and nuclear abundances of the plasma depends on stellar evolution conditions, and cross sections for the various reactions are not always known accurately (and this depends also on the extent of the nuclear reactions network taken into account in the computation).

Since the nuclear reactions relevant to our problem and to the production of gamma rays require energies of about 10 MeV per nucleus, our interest is limited to the inner regions of the accretion flow, i.e. regions around the compact object between about 100 Schwarzschild radii) and either the surface of the neutron star or the horizon of the black hole, depending on the nature of the compact object. For general purposes, we assume a mass of $1 \, M_{\odot}$ for the compact object, unless a specific case is considered.

In this work we consider a number of relatively simple accretion disk models:

• 1 - The Advection-Dominated Accretion Flow (ADAF) model proposed by Narayan and co-workers (Narayan & Yi 1994; Chen et al. 1995; Narayan et al. 1995; Narayan & Yi 1995), which has the added appeal that its temperature and density function are very simple and analytical expressions (Yi & Narayan 1997):
  

$$T_{\rm i} = 1.11 \times 10^{12} \, r^{-1}\ {\rm K} = 95.68 \, r^{-1} \; {\rm ~MeV}$$ (1)

where r is the dimensionless radial variable $r = R / R_{\rm S}$;

$$n = 6.4 \times 10^{18} \; \alpha^{-1} \; m^{-1} \; \dot m \; r^{-3/2} \; {\rm cm}^{-3}$$ (2)

where m is the dimensionless mass measured in units of a solar mass ( $m = M / M_{\odot}$), $\dot m$ is the dimensionless accretion rate measured in units of the Eddington accretion rate $\dot m = \dot M / \dot M_{\rm Edd} = {\dot M} / {1.4 \times 10^{17} m}~~ {\rm g/s}$ (in this work we will consider values of $\dot M$ in the range of $10^{-10} \ M_{\odot}/\rm yr$- $10^{-8} \ M_{\odot}/\rm yr$), taking $\beta$ (the ratio of gas pressure to total pressure) to equal 1/2 (as in Yi & Narayan 1997); the central factor $\alpha$ is taken to equal either 0.3 or 0.1 (following Narayan & Yi 1994).

Furthermore, it must be noted that in this model the value of the electron temperature does not affect our results, which depend mainly on the profile of the ion temperature $T_{\rm i}$(r).




• 2 - The Advection-Dominated Inflow-Outflow Solutions proposed by Blandford and Begelman (1998), which consist of a "generalized" ADAF model where only a small fraction of the gas initially supplied ends up falling onto the compact object, and where the energy released is transported radially outward and effectively becomes a wind, driving away the rest of the accreted material.

  In this family of solutions, a central assumption is the radial dependence of the accretion rate as ${\dot m(r) \propto r^p, \, 0 \le p < 1 \; }$. In the present work, we take the "gasdynamical wind" (case iv of Blandford & Begelman 1998) solution, i.e. $p = 1/2, \, \epsilon = 1/2$, which leads to a density function $n \propto r^{-1}$; more precisely:

  
  

$$n = 2.18 \times 10^{19} \; \alpha^{-1} \; \frac{(4.52 \times 10^{8}) \times \dot M} {m r} \; \rm cm^{-3} \; .$$ (3)

Note that this special form of the density function also corresponds to the solution obtained by Kazanas et al. (1997) in fitting the time lags in similar, compact X-ray accreting sources.

Another important equation is that of the disk height h (in units of $R_{\rm S}$), which in the particular solution adopted here, is given by:

$$h = 0.447 \, \times 3 \, m \, r.$$ (4)

Also, the radial velocity is

$$v_{\rm r} = 0.52 \; \alpha \; r^{- \frac{1}{2}} \; c \; \rm cm/s.$$ (5)

Finally, the ion temperature profile is the same as in ADAF.




• 3 - The Two-Temperature Shapiro-Lightman-Eardley (1976) Model, for which the expressions are given by:

  
  

$$T_{\rm i} = 5 \times 10^{11} \; M_*^{- \frac{5}{6}} \, \dot M... ...ac{7}{6}} \, \phi^{\frac{5}{6}} \, r_*^{- \frac{5}{4}} \;\rm K$$ (6)

$$T_{\rm e} = 7 \times 10^8 \; M_*^{\frac{1}{6}} \, \dot M_*^{-... ...ac{1}{6}} \, \phi^{- \frac{1}{6}} \, r_*^{\frac{1}{4}} \;\rm K$$ (7)

$$h = 10^5 \; M_*^{\frac{7}{12}} \, \dot M_*^{- \frac{5}{12}} \... ...{7}{12}} \, \phi^{\frac{7}{12}} \, r_*^{\frac{7}{8}} \; \rm cm$$ (8)

$$\rho = 5 \times 10^{-5} \; M_*^{- \frac{3}{4}} \, \dot M_*^{-... ...} \, \phi^{- \frac{1}{4}} \, r_*^{- \frac{9}{8}} \;\rm g/cm^3,$$ (9)

where $M_* = M /3 ; \phi = 1 -\sqrt{3R_{\rm S}/R} = 1 - \sqrt{3/r} ; \dot M_* = \dot M / 10^{17} {\rm g/s} ; r_* = 2R/R_{\rm S} = 2 r.$




• 4 - The uniform-temperature model, similar to the one used in the Guessoum & Kazanas (1990) neutron-viscosity model, where $T_{\rm i}$ is set by a viscosity condition but is taken to be uniform in the disk, and $T_{\rm e}$ is chosen arbitrarily (usually between 0.1 and 0.5 MeV); the density is then obtained from an energy balance requirement (viscous heating of the ions equal to Coulomb energy transfer from the ions to the electrons). In the Guessoum & Kazanas model, the following relations were derived:
  

$$n = \frac{3.375 \times 10^{25}}{r^2} \sqrt{\frac{\dot m}{m^3 \, f_{\rm th}}}$$ (10)

where $f_{\rm th}$ is the ion-electron Coulomb energy transfer function (Dermer 1986),

and

$$t_{\rm visc} = \frac{4\pi}{3} m_{\rm i} \, R^3 \frac{n}{\dot m}$$ (11)

where $m_{\rm i}$ is the mass of the ion.

Finally we note that in each case the system is taken to be in steady-state, whereby the accretion and in-fall are constant in time, and thus the neutron production and gamma-ray emission are steady.

  
2.1 The nuclear reactions

Assuming an initial composition for the accreting plasma, that is some initial fractions of hydrogen and helium (90% H, 10% He in the "normal'' case, and 10% H, 90% He in the "helium-rich case", which would correspond to a Wolf-Rayet secondary star companion), we compute the rates of the main nuclear reactions which the ions (the protons, alphas, ³He and ²H nuclei) can undergo:

$${\rm p} + \alpha \longrightarrow {}^3{\rm He} + {}^2{\rm H}$$

$$\alpha + \alpha \longrightarrow {}^7{\rm Li} + {\rm p}$$

$${\rm p} + {}^3{\rm He} \longrightarrow 3{\rm p} + {\rm n}$$

$$\alpha + \alpha \longrightarrow {}^7{\rm Be} + \rm n$$

$$\alpha + {}^3{\rm He} \longrightarrow \alpha + 2{\rm p} + {\rm n}$$

$${\rm p} + {}^2{\rm H} \longrightarrow 2{\rm p} + {\rm n}.$$

The first two reactions contributing to the destruction of helium (our source of neutrons), and the last four reactions are the actual neutron-producing processes. We disregard all high-energy neutron-production from proton-proton collisions. The cross sections are essentially the same as those used in Guessoum & Kazanas (1999), and the reaction rates are calculated through the usual non-relativistic expression for binary processes ( $r_{ij} = n_i n_j/(1 + \delta_{ij}) <\sigma_{ij} v_{ij}>$, the averaging here is performed over thermal distributions for the ions).

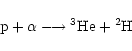
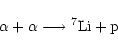
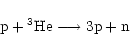
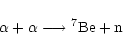
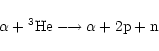
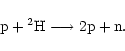
We then let the plasma evolve over the dynamical timescale $t_{\rm d}$, with its temperature and density set by the disk structure equations given above for each model, as the material sinks in the gravitational well. We use a simple numerical scheme of explicit finite-differencing to follow the abundances of the various species (the neutrons in particular). This calculation is performed for various values of the model parameters: $\dot M = 10^{-10}, \; 10^{-9} \;$ and $10^{-8} \; M_{\odot}/ {\rm yr}$; $\alpha = 0.3$ and 0.1; M = 1; etc. Note that since we are only interested in neutron production in the disk and not in any radiative processes, the electron temperature $T_{\rm e}$, whenever needed, is taken as a free parameter, usually equal to either 100 or 500 keV.

The escape of the neutrons is handled in the same way as in Aharonian & Sunyaev (1984) or Guessoum & Kazanas (1990), that is by computing the fraction of neutrons that have kinetic energies sufficient to overcome the gravitational binding to the compact object: $1/2 m_{\rm n} ({v_{\rm flow}} + {v_{\rm thermal}})^2 > G M m_{\rm n} / R$; this translates into a fraction of escaping neutrons given by Eqs. (13)-(15) of Guessoum & Kazanas (1990).

One final important aspect of the neutrons produced is their energy distribution. This aspect was addressed briefly in Guessoum & Kazanas (1999), where it was concluded that a thermal distribution of the neutrons with a temperature equal to that of the ions in the disk is reasonable. This point proves to be important not only for the escape fraction, but also for the interaction of those neutrons that reach the secondary star's atmosphere, since their various interactions there depend strongly on their kinetic energies.

  
2.2 Neutron production results in various disks

Before presenting results of neutron production for the various disk models, we first show the main characteristics of these models. Figures 1 show the plasma density n (in units of 10¹⁵ cm^-3), the ion temperature $T_{\rm i}$ (in units of MeV), the escape fraction of neutrons $f_{\rm esc}$, and the abundance of neutrons achieved in the disk, all as a function of $r = R / R_{\rm S}$, in the ADAF, ADIOS, SLE, and Uniform-$T_{\rm i}$(10 and 30 MeV), respectively, for disks with solar composition (90% H and 10% He) and an accretion rate of 10^-9 $M_{\odot }$/yr; for ADAF, ADIOS, and SLE the value of $\alpha$ in the figures is 0.1, and for the Uniform-$T_{\rm i}$ models the electron-temperature used for the figures is 0.5 MeV.

Figure 1: Plasma characteristics (density, ion temperature, escape fraction of neutrons, and abundance of neutrons) as a function of r, in the ADAF, ADIOS, SLE, and Uniform-$T_{\rm i}$ (10 and 30 MeV), assuming ${\dot M} = 10^{-9}~M_{\odot}$/yr, $\alpha = 0.1$, and $T_{\rm e} = 0.1$ MeV.

Table 1 presents the results of these calculations, showing the rates of neutron production in the ADAF-model case for various values of the viscosity parameter $\alpha$ and the mass accretion rate $\dot M$ (1a corresponds to a "normal'' composition; 1b corresponds to the "helium-rich" case). All the results shown correspond to $M = 1 \, M_{\odot}$ and $R \approx 100 \ R_{\rm S} \approx 10^7$ cm, though the actual results are mostly insensitive to the value of the outer radius of the disk, as most of the nuclear reactions and neutron production take place in the inner part (less than about 10 $R_{\rm S}$) of the accretion flow where the ion temperature is several tens of MeV.

Table 2 is equivalent to Table 1 in the ADIOS model. Table 3 corresponds to the SLE model; Tables 4 and 5 correspond to the uniform-$T_{\rm i}$ model, with $T_{\rm i}$ = 30 MeV and $T_{\rm i}$ = 10 MeV. Respectively.

It is interesting to note that the resulting neutron fluxes depend strongly on the models considered, but also are quite sensitive to the 3 disk parameters considered, namely $\alpha$, $\dot M$, and the initial composition of the plasma.

  

Table 1: Neutron production rate (in neutrons/s) in the ADAF Model, for initial a) 90% H and 10% He and b) 10% H and 90% He compositions.

  

Table 2: Neutron production rate in the ADIOS Model, for initial a) 90% H and 10% He and b) 10% H and 90% He compositions.

  

Table 3: Neutron production rate in the SLE Model, for initial a) 90% H and 10% He and b) 10% H and 90% He compositions.

  

Table 4: Neutron production rate in the uniform ion temperature model with $kT_{\rm i}$ = 30 MeV, for initial a) 90% H and 10% He and b) 10% H and 90% He compositions.

  

Table 5: Neutron production rate in the uniform ion temperature model with $kT_{\rm i}$ = 10 MeV, for initial a) 90% H and 10% He and b) 10% H and 90% He compositions.