The adapted SEI model reproduces the HM-effect in HD 77581/Vela X-1, and naturally explains the lack of any (clear) HM-effect observed in the dense wind system HD 153919/4U1700-37. Absorption components that are seen both in the strong wind lines and additional weaker lines in the UV spectrum of HD 77581/Vela X-1 and that could not be reproduced by the adapted SEI model can be explained by a photo-ionization wake. The orbital modulation of the resonance lines in the UV spectra of the five HMXBs studied here shows a clear trend of the size of the Strömgren zone to increase with higher X-ray luminosity.
The terminal velocity ![]() may be estimated from a comparison of an
appropriate model line profile with the observed line profile. It is best
derived from moderately saturated profiles, in which case the maximum
absorption in the
may be estimated from a comparison of an
appropriate model line profile with the observed line profile. It is best
derived from moderately saturated profiles, in which case the maximum
absorption in the ![]() line profile occurs at the terminal velocity.
line profile occurs at the terminal velocity.
The terminal velocity for HD 77581/Vela X-1 is thus estimated to be
![]() kms-1, much slower than previously reported (1105 kms-1 Prinja et al. 1990). For HD 153919/4U1700-37 we estimate
kms-1, much slower than previously reported (1105 kms-1 Prinja et al. 1990). For HD 153919/4U1700-37 we estimate
![]() kms-1 (Prinja et al. 1990: 1820 kms-1). These
values should be correct to within 100 kms-1. The low resolution IUE
spectra show that the wind in HDE 226868/Cyg X-1 is faster (marginally
resolved:
kms-1 (Prinja et al. 1990: 1820 kms-1). These
values should be correct to within 100 kms-1. The low resolution IUE
spectra show that the wind in HDE 226868/Cyg X-1 is faster (marginally
resolved:
![]() kms-1) than in Sk-Ph/LMC X-4 and Sk
160/SMC X-1 (unresolved:
kms-1) than in Sk-Ph/LMC X-4 and Sk
160/SMC X-1 (unresolved:
![]() kms-1, see also
Hammerschlag-Hensberge et al. 1984 for Sk 160/SMC X-1). HST/STIS spectra of
the N V, Si IV and C IV lines in Sk-Ph/LMC X-4 around
kms-1, see also
Hammerschlag-Hensberge et al. 1984 for Sk 160/SMC X-1). HST/STIS spectra of
the N V, Si IV and C IV lines in Sk-Ph/LMC X-4 around ![]() suggest a
terminal velocity of
suggest a
terminal velocity of ![]() kms-1, even though wind velocities up to
kms-1, even though wind velocities up to
![]() kms-1 occur (Kaper et al. in preparation).
kms-1 occur (Kaper et al. in preparation).
Single (galactic) O-type and early-B-type stars are known to have a fairly
constant ratio of terminal over escape velocity
![]() ,
where
,
where
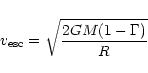 |
(20) |
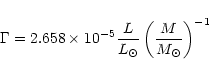 |
(21) |
The Strömgren zone could inhibit acceleration of the stellar wind material flowing through it, not only resulting in an ionization wake but possibly also leading to a slower terminal velocity of the wind. This scenario only works if the Strömgren zone is sufficiently large and the orbital period sufficiently short that all wind material leaving the star passes through the Strömgren zone before having reached the terminal velocity. The magellanic systems indeed must have very extended Strömgren zones leaving only a small region at the opposite side of the primary unaffected by the X-ray source (i.e. a shadow wind), and their orbital periods are rather short. However, the Strömgren zones in HD 77581/Vela X-1 and HD 153919/4U1700-37 are closed surfaces, and certainly do not occupy more than half of the circumstellar space. Within half their orbital periods of 4.5 and 1.7 days, respectively, their stellar winds ought to already have accelerated to velocities approaching the terminal velocity as if it were from a single star.
A viable alternative is that the ![]() factors for single stars are not
applicable to stars in interacting binaries. HMXBs primaries may have already
lost a significant fraction of their initial mantle mass, causing them to be
undermassive for their luminosity (Conti 1978; Kaper 2001). This seems to be
confirmed when comparing the primary star masses (Table 1) with Table 3 in
Howarth & Prinja (1989). Hence we may have under-estimated
factors for single stars are not
applicable to stars in interacting binaries. HMXBs primaries may have already
lost a significant fraction of their initial mantle mass, causing them to be
undermassive for their luminosity (Conti 1978; Kaper 2001). This seems to be
confirmed when comparing the primary star masses (Table 1) with Table 3 in
Howarth & Prinja (1989). Hence we may have under-estimated ![]() and
over-estimated
and
over-estimated
![]() .
.
| Primary |
|
|
||
| HDE 226868 | 30500 | 0.34 | 1.8-2.8 | |
| Sk-Ph | 36000 | 0.16 |
|
|
| Sk 160 | 26000 | 0.18 |
|
|
| HD 77581 | 23400 | 0.18 | 1.3 | 0.45 |
| HD 153919 | 37200 | 0.34 | 2.0 | 0.15 |
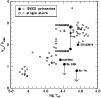 |
Figure 15: Ratio of terminal over escape velocity for the primary stars in the HMXBs studied here (solid dots), compared to single stars (circles) from Lamers et al. (1995). HMXB members have low terminal velocities for their effective temperatures. |
A turbulence description has been employed to account for material at
velocities deviating from the bulk flow that obeys a velocity law according to
standard radiation-driven wind theory. The ![]() is the typical deviation
in units of
is the typical deviation
in units of ![]() .
To approximately describe both the undisturbed wind
and X-ray ionized components in the line profiles of HD 77581/Vela X-1 a very
large value for
.
To approximately describe both the undisturbed wind
and X-ray ionized components in the line profiles of HD 77581/Vela X-1 a very
large value for ![]() needs to be invoked (
needs to be invoked (
![]() ), whereas for
HD 153919/4U1700-37 a much smaller value suffices (
), whereas for
HD 153919/4U1700-37 a much smaller value suffices (
![]() ). In
absolute terms the turbulence in these two HMXBs is very similar, though:
). In
absolute terms the turbulence in these two HMXBs is very similar, though:
![]() and 255 kms-1, respectively. These values are typical
for winds from O-type stars for which
and 255 kms-1, respectively. These values are typical
for winds from O-type stars for which
![]() has been found to be
largely independent of
has been found to be
largely independent of
![]() (Groenewegen et al. 1989). As mentioned
before, we find indications for the deviations from the monotonic velocity law
to resemble a shocked wind structure rather than uniform turbulence.
(Groenewegen et al. 1989). As mentioned
before, we find indications for the deviations from the monotonic velocity law
to resemble a shocked wind structure rather than uniform turbulence.
| Line |
|
T | A |
|
|
|
|
| HD 77581/Vela X-1: | |||||||
| N V | 1238.821 | 0.152 | 3 |
|
|
|
|
| Si IV | 1393.755 | 0.528 | 300 |
|
|
|
|
| C IV | 1548.20 | 0.194 | 200 |
|
|
|
|
| Al III | 1854.716 | 0.560 | 20 |
|
|
0.3 | <1 |
| HD 153919/4U1700-37: | |||||||
| N V | 1238.821 | 0.152 | 30 |
|
|
|
|
| Si IV | 1393.755 | 0.528 |
|
|
|
|
|
| C IV | 1548.20 | 0.194 | 5000 |
|
|
|
|
In principle, the mass-loss rate may be estimated from the integrated optical
depth T of a resonance line:
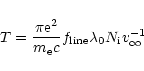 |
(22) |
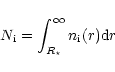 |
(23) |
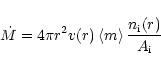 |
(24) |
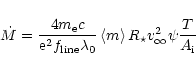 |
(25) |
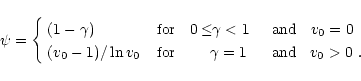 |
(26) |
In practice, however, the limited knowledge of the ionization balance in the
winds of OB supergiants makes the derived mass-loss rates highly unreliable.
Instead, the ionization fractions of the ions may be derived when other, more
reliable estimates for the mass-loss rate are available. For resonance lines
the excitation fraction of the ion that produces the line is unity, and the
ion abundance ![]() is the product of the ionization fraction
is the product of the ionization fraction
![]() and elemental abundance A (by number). Assuming solar
abundances (Anders & Grevesse 1989), the ionization fraction may be derived
using Eq. (25).
and elemental abundance A (by number). Assuming solar
abundances (Anders & Grevesse 1989), the ionization fraction may be derived
using Eq. (25).
Lamers et al. (1999) found
![]() to depend on both radiation
temperature and density, with the radiation temperature scaling approximately
linearly with
to depend on both radiation
temperature and density, with the radiation temperature scaling approximately
linearly with
![]() .
The empirical dependencies of
.
The empirical dependencies of
![]() on
density were contrary to the expected ionization balance, however, and it was
argued that the empirical relations may suffer from selection effects.
Therefore, we only consider their empirical relations between
on
density were contrary to the expected ionization balance, however, and it was
argued that the empirical relations may suffer from selection effects.
Therefore, we only consider their empirical relations between
![]() and
and
![]() .
.
Schröder et al. (in preparation) model the H![]() profiles of OB
supergiants in HMXBs. They derive mass-loss rates for HD 77581
(
profiles of OB
supergiants in HMXBs. They derive mass-loss rates for HD 77581
(
![]() yr-1) and HD 153919
(
yr-1) and HD 153919
(
![]() yr-1), which are comparable to
those derived for single stars of similar spectral type (Howarth & Prinja
1989). Combining their results with the results from the SEI models,
ionization fractions
yr-1), which are comparable to
those derived for single stars of similar spectral type (Howarth & Prinja
1989). Combining their results with the results from the SEI models,
ionization fractions
![]() are estimated for the N4+,
Si3+ and C3+ (and Al2+) ions in the (undisturbed) stellar winds
of HD 77581 and HD 153919 (Table 5). These are then compared with the ionization
fractions estimated from Fig. 3 in Lamers et al. (1999), taking into account
their lower and upper limits.
are estimated for the N4+,
Si3+ and C3+ (and Al2+) ions in the (undisturbed) stellar winds
of HD 77581 and HD 153919 (Table 5). These are then compared with the ionization
fractions estimated from Fig. 3 in Lamers et al. (1999), taking into account
their lower and upper limits.
The ion fractions derived from the SEI modelling for HD 77581/Vela X-1 are in agreement with the predictions for single stars by Lamers et al. (1999), except for the N4+ abundance which is observed to be an order of magnitude higher than predicted. This may be due to either super-ionization or nitrogen over-abundance (or both). Auger ionization (Cassinelli & Olson 1979) is sometimes invoked to explain strong N V resonance lines. Unless the density becomes very high, Auger ionization increases with the velocity in the wind, and may originate in the high-velocity extrema of a shocked wind. This might mimic a moderate increase of ionization fraction with distance, as required to reproduce the observed line profile and variability of the N V line in HD 77581/Vela X-1. On the other hand, nitrogen over-abundance at the surface of HD 77581 may have resulted from (i) the transfer in the past of nitrogen-enriched material from the progenitor of Vela X-1 onto HD 77581, or (ii) strong mass loss exposing deeper layers mixed with the products of nuclear burning. Kaper et al. (1993) note that HD 77581 might be a BN star.
For HD 153919/4U1700-37 the opposite is found: the observed ionization
fraction of N4+ agrees very well with the predictions, whereas the
ionization fractions of Si3+ and C3+ are observed to be (much)
higher than predicted. Perhaps these are the dominant ionization states for
silicon and nitrogen in the stellar wind of HD 153919, rather than Si4+and C4+. Still, an ionization fraction
![]() for
Si3+ is unrealistic for a multi-level atom, and hence the SEI model must
have over-estimated the integrated optical depth of the Si IV line in
HD 153919/4U1700-37. If indeed the degree of ionization in the wind of
HD 153919 is lower than that predicted for single stars, this would mean that
- like in the wind of HD 77581 - N4+ is in fact overabundant in the
wind of HD 153919.
for
Si3+ is unrealistic for a multi-level atom, and hence the SEI model must
have over-estimated the integrated optical depth of the Si IV line in
HD 153919/4U1700-37. If indeed the degree of ionization in the wind of
HD 153919 is lower than that predicted for single stars, this would mean that
- like in the wind of HD 77581 - N4+ is in fact overabundant in the
wind of HD 153919.
The size of the Strömgren zone, indicated by a particular value of the
parameter q, is related to the ionization parameter ![]() as
as
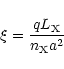 |
(27) |
Accretion of matter onto a star moving through a medium was first described by
Bondi & Hoyle (1944). Their concept was applied to HMXBs by Davidson &
Ostriker (1973). In an HMXB the compact object has a velocity
![]() relative to the stellar wind flow:
relative to the stellar wind flow:
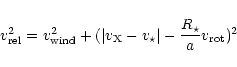 |
(28) |
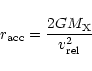 |
(29) |
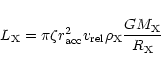 |
(30) |
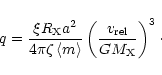 |
(31) |
| HMXB |
|
|
|
| HDE 226868/Cyg X-1 | 1.7 | 1.7-5.0 |
|
| Sk-Ph/LMC X-4 | 2.7 | <1.6-4.5 | <2.7 |
| Sk 160/SMC X-1 | 2.9 | <6.3-17 | |
| HD 77581/Vela X-1 | 2.7 | 10-24 | 2.9 |
| HD 153919/4U1700-37 | 2.0 | 177-215 | >4.0 |
From the time sequence of the integrated line variability (Figs. 1 and 2) and the modelling of the line profile variability it is already clear that the Strömgren zone is largest for Sk-Ph/LMC X-4 and especially Sk 160/SMC X-1: their zones must extend far beyond the primary as seen from the X-ray source, and the stellar wind is undisturbed only in a small shadow region behind the primary. The Strömgren zone is smaller but still very extended for HDE 226868/Cyg X-1 where the variability due to the HM-effect is continuous over the orbit. HD 77581/Vela X-1 has an again smaller and now closed Strömgren zone, but it still occupies a considerable fraction of the wind volume. The (by far) smallest Strömgren zone is found for HD 153919/4U1700-37.
The critical and expected sizes of the Strömgren zones for the five HMXBs
are listed in Table 6. The
![]() is calculated assuming a
velocity law according to Eq. (2) with v0=0.01 and
is calculated assuming a
velocity law according to Eq. (2) with v0=0.01 and ![]() .
The
.
The
![]() is calculated assuming
is calculated assuming ![]() (Hatchett & McCray 1977) for a
typical X-ray spectrum,
(Hatchett & McCray 1977) for a
typical X-ray spectrum, ![]() ,
and
,
and
![]() km for
km for
![]() and
and
![]() .
The range in values results from
either assuming co-rotation of the primary with the orbit or no rotation of
the primary (and the uncertainty about
.
The range in values results from
either assuming co-rotation of the primary with the orbit or no rotation of
the primary (and the uncertainty about ![]() for Cyg X-1, LMC X-4 and SMC
X-1). The observed sizes of the Strömgren zone are in reasonable agreement
with the expected sizes that, in general, seem to have been somewhat
under-estimated. This could easily be solved if for instance the accretion
efficiency
for Cyg X-1, LMC X-4 and SMC
X-1). The observed sizes of the Strömgren zone are in reasonable agreement
with the expected sizes that, in general, seem to have been somewhat
under-estimated. This could easily be solved if for instance the accretion
efficiency ![]() were twice as large. In particular,
were twice as large. In particular, ![]() increases with
larger mass and smaller radius of the compact object (Shakura & Sunyaev
1973), which would yield an accretion efficiency for the black-hole candidate
Cyg X-1 significantly larger than 10%.
increases with
larger mass and smaller radius of the compact object (Shakura & Sunyaev
1973), which would yield an accretion efficiency for the black-hole candidate
Cyg X-1 significantly larger than 10%.
Copyright ESO 2001