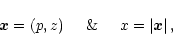 |
(1) |
The high-mass X-ray binary is described as a spheroidal early-type star with a
spherically symmetric radially outflowing wind, and an orbiting X-ray point
source. The used coordinate system is based on the impact parameter p and
the line-of-sight parameter z, in units of the stellar radius and with the
center of the early-type star at (0,0):
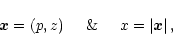 |
(1) |
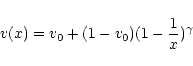 |
(2) |
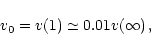 |
(3) |
The X-ray point source at position
![]() affects the normal
abundance q'(x) of a certain ion in the wind. The degree at which the wind
is disturbed is set by the parameter
affects the normal
abundance q'(x) of a certain ion in the wind. The degree at which the wind
is disturbed is set by the parameter
![]() (Hatchett & McCray 1977):
(Hatchett & McCray 1977):
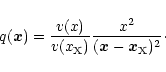 |
(4) |
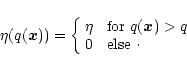 |
(5) |
A negative value for ![]() enhances the abundance of the ion within the
Strömgren zone. The X-ray point source is located inside a closed surface
of constant q if
enhances the abundance of the ion within the
Strömgren zone. The X-ray point source is located inside a closed surface
of constant q if
| (6) |
![\begin{displaymath}%
q_{\rm critical} =\lim_{\begin{array}{c}
\\ [-6mm]
{\scrip...
...le p = 0}
\end{array}}
q({x}) = \frac{1}{v(x_{\rm X})} \cdot
\end{displaymath}](/articles/aa/full/2001/32/aah2663/img94.gif) |
(7) |
| (8) |
| (9) |
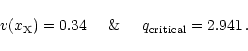 |
(10) |
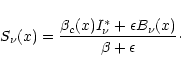 |
(11) |
| (12) |
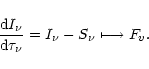 |
(13) |
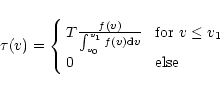 |
(14) |
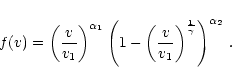 |
(15) |
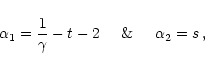 |
(16) |
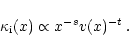 |
(17) |
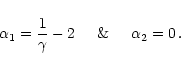 |
(18) |
The intrinsic line profile resembles a Gaussian, with isotropic broadening
![]() due to the thermal and turbulent motions - hereafter referred
to as the "turbulence'' (Lamers et al. 1987):
due to the thermal and turbulent motions - hereafter referred
to as the "turbulence'' (Lamers et al. 1987):
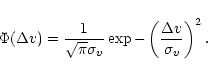 |
(19) |
In the case of doublets (most of the important UV resonance lines are doublets), depending on the doublet separation the source function of the red component includes a contribution from the blue component. Except for this coupling, the principle of the SEI code is the same as for singlets (Lamers et al. 1987). However, since we now include a Strömgren zone we can no longer use a one-dimensional radial grid to calculate the source function of the red component (as is the case for the SEI method). The contribution of the source function of the blue component to the source function of the red component depends on whether the coupled blue component points are situated inside the Strömgren zone. Hence the radial profile of the source function depends on the position of the Strömgren zone. This is solved by replacing the one-dimensional grid when calculating the source function of the red component by a two-dimensional axi-symmetric grid.
The SEI method allows the inclusion of a photospheric component in the input line spectrum, but we did not use this option in the model profiles shown below.
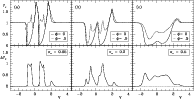 |
Figure 5:
The effect of turbulence: same as Fig. 4, but for q=3.2 and
different levels of wind turbulence
|
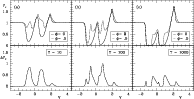 |
Figure 6: From weak to strong: same as Fig. 4, but for q=3.2 and illustrating the effect of increased integrated optical depth T. |
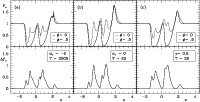 |
Figure 7:
Same as Fig. 4, but for q=3.2 and illustrating the effect of
different parameterisations of the optical depth (via |
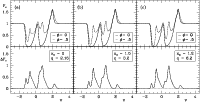 |
Figure 8:
Same as Fig. 4, but for q=3.2 and illustrating the effect of
different distances |
The accuracy of the calculations depends on the grid ![]() ,
which
samples the intrinsic line profile. The number of points used in the grid is
,
which
samples the intrinsic line profile. The number of points used in the grid is
![]() .
In the original code a choice of
.
In the original code a choice of
![]() yields
satisfactory results, but if a Strömgren zone is included this value
should be some two orders of magnitude larger to suppress the numerical noise.
Stronger turbulence demands larger
yields
satisfactory results, but if a Strömgren zone is included this value
should be some two orders of magnitude larger to suppress the numerical noise.
Stronger turbulence demands larger
![]() .
.
To illustrate how the important model parameters affect the shape of the
spectral line profile, model spectra are shown for a hypothetical resonance
doublet of a HMXB system. The canonical model consists of a HMXB with
![]() ,
wind velocity law with
,
wind velocity law with ![]() ,
v0=0.01 and
,
v0=0.01 and
![]() ,
doublet separation of 1.5, integrated optical depth of the blue component of
T=100 (twice that of the red component), dominant ionization stage in the
uniformly ionized undisturbed wind (t,s=0), no additional source of emission
(
,
doublet separation of 1.5, integrated optical depth of the blue component of
T=100 (twice that of the red component), dominant ionization stage in the
uniformly ionized undisturbed wind (t,s=0), no additional source of emission
(
![]() ), no photospheric absorption profile, and a Strömgren zone
of size q=3.2.
), no photospheric absorption profile, and a Strömgren zone
of size q=3.2.
Figures 4 to 8 illustrate the effect of varying several of these parameters.
The top panels present the UV resonance profiles at two orbital phases: at
X-ray eclipse (![]() ,
drawn line) a large fraction of the Strömgren
zone is behind the OB supergiant so that only a small part of the observable
stellar wind is affected. When the X-ray source is located in the absorbing
column in front of the OB supergiant (
,
drawn line) a large fraction of the Strömgren
zone is behind the OB supergiant so that only a small part of the observable
stellar wind is affected. When the X-ray source is located in the absorbing
column in front of the OB supergiant (![]() ), the blue-shifted absorption
trough is reduced in strength. Note that also the emission peak of the P-Cygni
profile is affected, though less pronounced because the wind volume
contributing to the P-Cygni emission is much larger in comparison to the
volume of the absorbing column. The bottom panels show the difference spectra
(
), the blue-shifted absorption
trough is reduced in strength. Note that also the emission peak of the P-Cygni
profile is affected, though less pronounced because the wind volume
contributing to the P-Cygni emission is much larger in comparison to the
volume of the absorbing column. The bottom panels show the difference spectra
(![]() minus
minus ![]() ).
).
The size q of the Strömgren zone strongly affects the spectral line
variability (Fig. 4). Small Strömgren zones (large q) leave little
trace in the spectral line profile, apart from some diminished absorption at
![]() at velocities between about
at velocities between about
![]() and 0 (i.e. not centred
at
and 0 (i.e. not centred
at
![]() ). A larger Strömgren zone enhances the HM-effect
especially near velocities
). A larger Strömgren zone enhances the HM-effect
especially near velocities
![]() ,
also reducing the absorption in the
blue wing of the line profile, and reduces the emission at positive velocities
at
,
also reducing the absorption in the
blue wing of the line profile, and reduces the emission at positive velocities
at ![]() (notably in the red component of the doublet). Saturation is not
maintained for Strömgren zones that cover a significant fraction of the
hemisphere in front of the star. However, open Strömgren zones leave only
a small area behind the primary unaffected (in the most extreme case this is a
shadow wind), and hence cause diminished absorption and emission at all
orbital phases, thereby reducing the contrast in line profile shape between
transit and eclipse of the X-ray source. The appearance of the HM-effect is
most prominent for
(notably in the red component of the doublet). Saturation is not
maintained for Strömgren zones that cover a significant fraction of the
hemisphere in front of the star. However, open Strömgren zones leave only
a small area behind the primary unaffected (in the most extreme case this is a
shadow wind), and hence cause diminished absorption and emission at all
orbital phases, thereby reducing the contrast in line profile shape between
transit and eclipse of the X-ray source. The appearance of the HM-effect is
most prominent for
![]() .
The definition of q allows a
Strömgren zone extending into the X-ray shadow behind the supergiant;
obviously, this can only happen if scattering of X-rays by ions in the stellar
wind is important.
.
The definition of q allows a
Strömgren zone extending into the X-ray shadow behind the supergiant;
obviously, this can only happen if scattering of X-rays by ions in the stellar
wind is important.
The presence of turbulence in the wind causes the line profile to broaden,
which results in less pronounced emission (Fig. 5). The HM-effect is also
smoothed in velocity space. The amplitude of variability at positive
velocities and between 0 and ![]() decreases, whilst the amplitude of
variability in the blue wing (
decreases, whilst the amplitude of
variability in the blue wing (
![]() )
increases. The blue wing
variability becomes dominant in the case of strong turbulence. In the absence
of turbulence it is difficult to hide the HM-effect unless the Strömgren
zone is much smaller than the projected stellar disk.
)
increases. The blue wing
variability becomes dominant in the case of strong turbulence. In the absence
of turbulence it is difficult to hide the HM-effect unless the Strömgren
zone is much smaller than the projected stellar disk.
Greater optical depth enhances the extent to which the absorption is
maintained when the Strömgren zone moves through the line of sight (Fig. 6). Note that for heavily saturated lines with turbulence, as for unsaturated
lines, it is not straightforward to determine the exact value of ![]() ,
and careful modelling is required.
,
and careful modelling is required.
The ionization stage of the ion, relative to the dominant ionization stage in
the (undisturbed) wind is of importance for the parameterisation and
normalisation of the optical depth. If the ion corresponds to an ionization
stage that is one level below the dominant ionization stage, then
![]() instead of -1 in the canonical example (see Eq. (16)). For the
same integrated optical depth, this would yield unsaturated and rather
triangular shaped absorption profiles with little emission. In the opposite
case, if the ion corresponds to one level above the dominant ionization stage,
then
instead of -1 in the canonical example (see Eq. (16)). For the
same integrated optical depth, this would yield unsaturated and rather
triangular shaped absorption profiles with little emission. In the opposite
case, if the ion corresponds to one level above the dominant ionization stage,
then
![]() .
This yields a heavily saturated line profile with stronger
emission and somewhat enhanced HM-effect in the absorption part between
.
This yields a heavily saturated line profile with stronger
emission and somewhat enhanced HM-effect in the absorption part between
![]() and
and ![]() ,
compared to the canonical case. From the
normalisation of the optical depth (Eqs. (14) and (15)) it follows that
,
compared to the canonical case. From the
normalisation of the optical depth (Eqs. (14) and (15)) it follows that ![]() at
at
![]() (=v1) is 0.010, 0.22, or 1.0 for
(=v1) is 0.010, 0.22, or 1.0 for
![]() ,
-1 and 0,
respectively. Scaling the total optical depth T to 2200 and 22 for
,
-1 and 0,
respectively. Scaling the total optical depth T to 2200 and 22 for
![]() and 0, respectively, the line profiles and appearance of the
HM-effect (Fig. 7) are similar to the canonical case. It may therefore be
difficult to distinguish between different values of
and 0, respectively, the line profiles and appearance of the
HM-effect (Fig. 7) are similar to the canonical case. It may therefore be
difficult to distinguish between different values of ![]() ,
and prior
knowledge of the dominant ionization species is required.
,
and prior
knowledge of the dominant ionization species is required.
The parameterisation of the optical depth involves the velocity law, and hence
the parameter ![]() .
Changing
.
Changing ![]() from 1 to 0.5 requires rescaling to
q=1.87,
from 1 to 0.5 requires rescaling to
q=1.87,
![]() and T=22 (Eqs. (4) and (15)). The resulting variability
is not exactly a scaled version of the canonical case (Fig. 7), because qdepends on both v and x. Most notably, the blue wing HM-effect is stronger
and saturation more difficult to maintain.
and T=22 (Eqs. (4) and (15)). The resulting variability
is not exactly a scaled version of the canonical case (Fig. 7), because qdepends on both v and x. Most notably, the blue wing HM-effect is stronger
and saturation more difficult to maintain.
A different distance ![]() of the X-ray source implies that different
parts of the wind are probed. Changing to
of the X-ray source implies that different
parts of the wind are probed. Changing to
![]() and 2.0 requires
rescaling to q=6.2 and 2.15, respectively. Increasing the distance of the
X-ray source enhances the HM-effect in the blue wing at the expense of the
HM-effect in the absorption part between
and 2.0 requires
rescaling to q=6.2 and 2.15, respectively. Increasing the distance of the
X-ray source enhances the HM-effect in the blue wing at the expense of the
HM-effect in the absorption part between
![]() and
and ![]() ,
and
also makes it more difficult for a saturated line to remain saturated (Fig. 8). If the X-ray source is located close to the primary, then the HM-effect in
the emission at positive velocities is less pronounced.
,
and
also makes it more difficult for a saturated line to remain saturated (Fig. 8). If the X-ray source is located close to the primary, then the HM-effect in
the emission at positive velocities is less pronounced.
Copyright ESO 2001