| 1998 | 2000 (except 4-5/02) | 4-5/02/2000 | |||||||||||||
|
|
|
|
|
|
|
||||||||||
|
|
|
|
|
|
|
||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
The statistics used for extracting the Mkn 421 spectra are given in Table B.1. With the same notations used in this paper, we write:
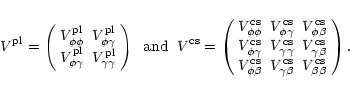
In the power-law hypothesis, the energy ![]() at which the values of
at which the values of
![]() et
et
![]() are decorrelated writes:
are decorrelated writes:
![\begin{displaymath}E_{\rm d}=\exp\left[\frac{V_{\phi\gamma}^{\rm pl}}{\phi_0^{\rm pl}V_{\gamma\gamma}^{\rm pl}}\right]\:{\rm TeV}.
\end{displaymath}](/articles/aa/full/2001/30/aah2794/img407.gif)
In the curved shape hypothesis, the energy-dependent exponent
![]() has a minimal error at the energy
has a minimal error at the energy
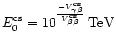 ;
the corresponding value of
;
the corresponding value of
![]() writes
writes
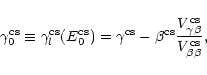
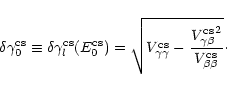
Copyright ESO 2001