The complete data sample consists of observations taken between December, 1996, and June, 2000.
During these periods, the source was systematically observed in a range of zenith angle extending from close to the Zenith up to
![]() .
The intensity of the source did not influence the observation strategy.
However, a selection based on criteria requiring clear moonless nights and stable detector operation has been applied:
this leaves a total of 139 hours of on-source (ON) data, together with 57 hours on control (OFF) regions.
The different light curves of the four observation periods are shown in Fig. 3. We used a
differential index of -2.9, which is representative of all spectral measurements presented in Sect. 3.2,
to estimate the integral flux above
.
The intensity of the source did not influence the observation strategy.
However, a selection based on criteria requiring clear moonless nights and stable detector operation has been applied:
this leaves a total of 139 hours of on-source (ON) data, together with 57 hours on control (OFF) regions.
The different light curves of the four observation periods are shown in Fig. 3. We used a
differential index of -2.9, which is representative of all spectral measurements presented in Sect. 3.2,
to estimate the integral flux above
![]() for all data, especially those taken far from the Zenith: this procedure is
detailed in Appendix A.2.
for all data, especially those taken far from the Zenith: this procedure is
detailed in Appendix A.2.
As can be seen in Fig. 3, the flux of Mkn 421 changed significantly between
1996-97 and 1997-98: almost quiet during the first period (with a mean flux
![]() ),
the source showed a higher mean activity during the second period (
),
the source showed a higher mean activity during the second period (
![]() ), with small bursts
in January and March sometimes showing up in excess of the steady flux from the Crab nebula (which is
), with small bursts
in January and March sometimes showing up in excess of the steady flux from the Crab nebula (which is
![]() above
above
![]() ,
see Piron 2000).
In 1998-99, the mean VHE emission of Mkn 421 (
,
see Piron 2000).
In 1998-99, the mean VHE emission of Mkn 421 (
![]() )
decreased to a level comparable to that of 1996-97. In spite of some activity detected during the winter, the weather conditions
in Thémis caused a very sparse source coverage. Nevertheless in the beginning of 2000
Mkn 421 showed a remarkable increase in activity, exhibiting a series of huge
bursts. As seen in Fig. 3, the bursts recorded in January and February
2000 clearly appear as the highest ever seen by CAT from this source
in four years with a nightly-averaged integral flux culminating at
)
decreased to a level comparable to that of 1996-97. In spite of some activity detected during the winter, the weather conditions
in Thémis caused a very sparse source coverage. Nevertheless in the beginning of 2000
Mkn 421 showed a remarkable increase in activity, exhibiting a series of huge
bursts. As seen in Fig. 3, the bursts recorded in January and February
2000 clearly appear as the highest ever seen by CAT from this source
in four years with a nightly-averaged integral flux culminating at ![]()
![]() and a large night-to-night
variability.
and a large night-to-night
variability.
VHE intra-night variability was also observed on a few occasions. For instance during the night of January 12-13,
the source intensity increased by a factor of 3.8 in ![]() 2 hours, from
2 hours, from ![]()
![]() to
to
![]()
![]() (with a
(with a ![]() per d.o.f of 2.5 for the absence of any variation), as can be seen in Fig. 3.1 (upper-left panel).
At the bottom of this figure, Mkn 421 light curves are also shown for three nights from the
3rd to the 5th February. While the fluxes recorded by CAT
during the first and last nights were stable, respectively
per d.o.f of 2.5 for the absence of any variation), as can be seen in Fig. 3.1 (upper-left panel).
At the bottom of this figure, Mkn 421 light curves are also shown for three nights from the
3rd to the 5th February. While the fluxes recorded by CAT
during the first and last nights were stable, respectively
![]() (over 4 hours) and
(over 4 hours) and
![]() (over 1 hour), the source activity
changed dramatically in a few hours during the second night (February 4-5). The CAT telescope started observation while the
source emission was at a level of
(over 1 hour), the source activity
changed dramatically in a few hours during the second night (February 4-5). The CAT telescope started observation while the
source emission was at a level of
![]() .
This flux is comparable to the historically highest
.
This flux is comparable to the historically highest ![]() flux ever
recorded, i.e., that of Mkn 501 during the night of April 16th, 1997
(Djannati-Ataï et al. 1999). In spite of the low source elevation (
flux ever
recorded, i.e., that of Mkn 501 during the night of April 16th, 1997
(Djannati-Ataï et al. 1999). In spite of the low source elevation (
![]() )
124
)
124 ![]() -ray
events with a signal significance of
-ray
events with a signal significance of
![]() were detected during the first 30 minutes of observation.
This may be compared to the 838
were detected during the first 30 minutes of observation.
This may be compared to the 838 ![]() -ray events and significance of
-ray events and significance of
![]() obtained during the whole night (see Fig. 1). After this first episode, the source intensity was reduced by a
factor of 2 in 1 hour and by a factor of 5.5 in 3 hours. In Fig. 3.1, each point stands for a
obtained during the whole night (see Fig. 1). After this first episode, the source intensity was reduced by a
factor of 2 in 1 hour and by a factor of 5.5 in 3 hours. In Fig. 3.1, each point stands for a
![]()
![]() observation but a finer binning in time does not show any additional interesting features, confirming that CAT
started observation after the flare maximum.
observation but a finer binning in time does not show any additional interesting features, confirming that CAT
started observation after the flare maximum.
 |
Figure 4:
Mkn 421 integral flux above
|
The data used in this section consist of a series of
![]()
![]() acquisitions for which a
acquisitions for which a ![]() -ray signal with significance greater
than
-ray signal with significance greater
than ![]() was recorded, and they have been further limited to zenith angles
was recorded, and they have been further limited to zenith angles
![]() ,
i.e., to a configuration for
which the detector calibration has been fully completed. The spectral study is thus based on 6.2 hours of on-source (ON) data taken in
1998 and 8.4 hours in 2000. Though this data selection reduces somewhat the total number of
,
i.e., to a configuration for
which the detector calibration has been fully completed. The spectral study is thus based on 6.2 hours of on-source (ON) data taken in
1998 and 8.4 hours in 2000. Though this data selection reduces somewhat the total number of ![]() -ray events, it provides a high
signal-to-noise ratio, minimizes systematic effects, and allows a robust spectral determination. Concerning
systematic effects, another favourable factor is the low night-sky background in the field of view due to the lack of
bright stars around the source.
-ray events, it provides a high
signal-to-noise ratio, minimizes systematic effects, and allows a robust spectral determination. Concerning
systematic effects, another favourable factor is the low night-sky background in the field of view due to the lack of
bright stars around the source.
Systematic errors are thus mainly due to the uncertainty on the absolute energy scale, which comes
from possible variations of the atmosphere transparency and light-collection efficiencies during the observation periods.
To a lesser extent, they are also due to limited Monte-Carlo statistics in the determination of the effective detection area.
These errors, assumed to be the same for all spectra, are implicitly considered in the following and they have been estimated from
detailed simulations (Piron 2000):
![]() %,
%,
![]() ,
and
,
and
![]() .
.
The 1998 and 2000 time-averaged spectra are shown in Fig. 5, both in the
power-law and curved shape hypotheses. The statistics used for their extraction are detailed in
Appendix B.1, the spectral parameters are summarized in Table 1, and their
covariance matrices are given in Appendix B.2. In each panel of Fig. 5,
the two lower plots give the ratio, in each bin of estimated energy, of the predicted number
of events to that which is observed both for the ![]() -ray signal (
-ray signal (![]() )
as well as for the hadronic background
(
)
as well as for the hadronic background
(![]() ).
This is another means to check the validity of the parameters estimation, and to compare between the two hypotheses
on the spectral shape.
).
This is another means to check the validity of the parameters estimation, and to compare between the two hypotheses
on the spectral shape.
 |
Figure 5:
Mkn 421 time-averaged spectra between 0.3 and
|
| Period |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
As can be seen in Fig. 5a, the power law accounts very well for the 1998 time-averaged spectrum. The likelihood
ratio value is low (
![]() ,
corresponding to a chance probability of 0.39), and the curvature term is compatible with zero
(
,
corresponding to a chance probability of 0.39), and the curvature term is compatible with zero
(
![]() ). Thus, we find the following differential spectrum:
). Thus, we find the following differential spectrum:
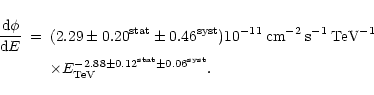
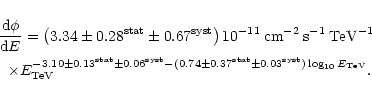
Copyright ESO 2001