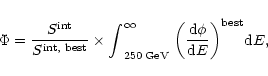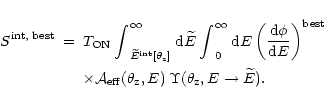Up: Temporal and spectral gamma-ray
Subsections
Appendix A.1: The spectral analysis procedure
Here we give the expression of the likelihood function
 used for spectral reconstruction, using the same notations as in
Sect. 2.3. We start with an assumption on the spectral shape by choosing a given law
used for spectral reconstruction, using the same notations as in
Sect. 2.3. We start with an assumption on the spectral shape by choosing a given law
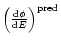 ,
which includes the set
,
which includes the set
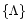 of parameters to fit.
Then, for each 2D-bin
of parameters to fit.
Then, for each 2D-bin
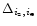 ,
corresponding to the zenith angle interval
,
corresponding to the zenith angle interval
![$[\theta^{{\rm min}}_{i_{\rm z}}, \theta^{{\rm max}}_{i_{\rm z}}]$](/articles/aa/full/2001/30/aah2794/img204.gif) and to the estimated energy interval
and to the estimated energy interval
![$[\widetilde{E}^{{\rm min}}_{i_{\rm e}}, \widetilde{E}^{{\rm max}}_{i_{\rm e}}]$](/articles/aa/full/2001/30/aah2794/img205.gif) ,
let us define:
The observed numbers
,
let us define:
The observed numbers
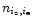 and
and
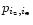 have Poissonian probability distributions
have Poissonian probability distributions
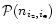 and
and
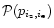 ,
respectively,
and the likelihood function is as follows:
,
respectively,
and the likelihood function is as follows:
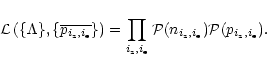 |
(A.2) |
The quantities
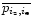 ,
which are unknown, can be determined by maximizing the function
,
which are unknown, can be determined by maximizing the function
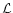 :
the relations
:
the relations
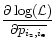
 0 lead to the solutions
0 lead to the solutions
![$\displaystyle\overline{p_{i_{\rm z}, i_{\rm e}}}=\frac{1}{2\beta_{i_{\rm z}}(\b...
...\rm z}}+1)p_{i_{\rm z}, i_{\rm e}}S_{i_{\rm z}, i_{\rm e}}^{{\rm pred}}}\right]$](/articles/aa/full/2001/30/aah2794/img235.gif) ,
with
,
with
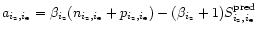 .
.
Finally, we reinject these expressions in Eq. (A.2), eliminate the "constant'' terms which only depend on
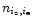 or
or
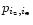 ,
and get:
,
and get:
| |
![$\textstyle \log\left[\mathcal{L}\left(\{\Lambda\}\right)\right]=\sum_{i_{\rm z}...
...\rm e}}^{{\rm pred}}+\beta_{i_{\rm z}}\overline{p_{i_{\rm z},i_{\rm e}}}\right)$](/articles/aa/full/2001/30/aah2794/img237.gif) |
|
|
| |
![$\textstyle +\;\;\;p_{i_{\rm z}, i_{\rm e}}\log\left(\overline{p_{i_{\rm z}, i_{...
...\overline{p_{i_{\rm z}, i_{\rm e}}}-S_{i_{\rm z}, i_{\rm e}}^{{\rm pred}}\Big].$](/articles/aa/full/2001/30/aah2794/img238.gif) |
|
(A.3) |
The
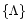 parameters, included in this expression through Eq. (A.1), are the only unknown quantities left: their values
are determined using an iterative procedure of maximization, which leads to the final fitted values and their covariance matrix V.
parameters, included in this expression through Eq. (A.1), are the only unknown quantities left: their values
are determined using an iterative procedure of maximization, which leads to the final fitted values and their covariance matrix V.
Appendix A.2: Integral flux determination
When computing an integral flux, one must again take care of the telescope detection threshold
increase with zenith angle
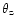 ;
thus, let us denote:
;
thus, let us denote:
-
![$\widetilde{E}^{\rm int}[\theta_{\rm z}]$](/articles/aa/full/2001/30/aah2794/img239.gif) for the unique energy which verifies
for the unique energy which verifies
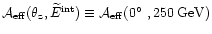 ;
;
-
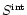 for the total number of
for the total number of 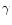 -ray events observed within the selection cuts with an estimated
energy above
-ray events observed within the selection cuts with an estimated
energy above
![$\widetilde{E}^{\rm int}[\theta_{\rm z}]$](/articles/aa/full/2001/30/aah2794/img239.gif) (
(
 is determined by a simple "ON-OFF'' subtraction), and
is determined by a simple "ON-OFF'' subtraction), and
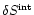 for its error.
for its error.
To convert
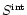 into the corresponding integral flux
into the corresponding integral flux 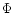 above
above
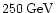 ,
we use the following proportionality relation:
,
we use the following proportionality relation:
where
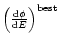 is the source differential spectrum measured as explained in Sect. 2.3,
and
is the source differential spectrum measured as explained in Sect. 2.3,
and
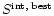 is the number of
is the number of 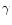 -ray events predicted from this law above
-ray events predicted from this law above
![$\widetilde{E}^{\rm int}[\theta_{\rm z}]$](/articles/aa/full/2001/30/aah2794/img239.gif) :
:
Finally, the error on 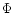 is simply estimated as
is simply estimated as
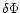 =
=
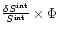 .
.


Up: Temporal and spectral gamma-ray
Copyright ESO 2001
![]() or
or
![]() ,
and get:
,
and get: