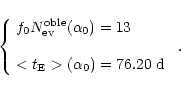Up: Constraints on the slope observables
We show now how it is possible to use the simple technique of the inverse problem to estimate the slope 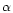 of the lens MF and the dark halo mass fraction f composed by MACHOs for each one of the models labelled by the codes previously explained. We consider data coming from the first 5.7 years of observations towards LMC by the MACHO collaboration (Alcock et al. 2000a), limiting ourselves to the thirteen events selected according to the so-called selection criteria A. These are high S/N events and are spatially distributed in a way which is consistent with the hypothesis that they are due to lenses belonging to our halo and not to LMC self lensing; we will discuss of this problem later on. For this set of events we have
of the lens MF and the dark halo mass fraction f composed by MACHOs for each one of the models labelled by the codes previously explained. We consider data coming from the first 5.7 years of observations towards LMC by the MACHO collaboration (Alcock et al. 2000a), limiting ourselves to the thirteen events selected according to the so-called selection criteria A. These are high S/N events and are spatially distributed in a way which is consistent with the hypothesis that they are due to lenses belonging to our halo and not to LMC self lensing; we will discuss of this problem later on. For this set of events we have
where
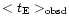 is simply the average value of the duration of the observed events. As a test of the correctness of this estimate we may note that
is simply the average value of the duration of the observed events. As a test of the correctness of this estimate we may note that
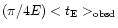 (with
(with
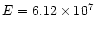 star-years) is exactly equal to
star-years) is exactly equal to
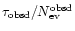 ,
as it has to be for the reasons we are going to explain later. We have then to estimate the uncertainties on the observed quantities. First, we consider the directly observed optical depth, and we simply use a method as similar as possible to the one proposed by the MACHO group itself for a very conservative estimate of the error on
,
as it has to be for the reasons we are going to explain later. We have then to estimate the uncertainties on the observed quantities. First, we consider the directly observed optical depth, and we simply use a method as similar as possible to the one proposed by the MACHO group itself for a very conservative estimate of the error on
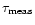 (Alcock et al. 1997a): we divide the observed events according to their duration
(Alcock et al. 1997a): we divide the observed events according to their duration 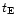 in bin of 10 days; in such a way
in bin of 10 days; in such a way
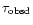 is more or less the same for events in the same bin and the errors are approximately poissonian. For each bin we estimate
is more or less the same for events in the same bin and the errors are approximately poissonian. For each bin we estimate
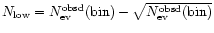 and
and
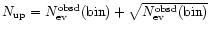 and define
and define
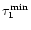 and
and
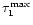 as the minimum and maximum value of
as the minimum and maximum value of 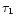 for the events in that bin (being
for the events in that bin (being
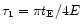 ). Then we estimate
). Then we estimate
At the end we find
The error on the optical depth turns out to be so large (
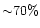 )
because of the limited number of events. Let us turn now to the error on the number of observed events. This simply comes from the low statistics and may be assumed to be poissonian, i.e.
)
because of the limited number of events. Let us turn now to the error on the number of observed events. This simply comes from the low statistics and may be assumed to be poissonian, i.e.
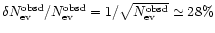 .
Finally, the error on
.
Finally, the error on
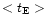 is obtained by propagating the error on
is obtained by propagating the error on
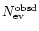 which gives us
which gives us
The observed quantities may be now compared to the theoretical ones evaluated in the previous section, which also take into account the detection efficiency in order to make the comparison meaningful. To do this we must first remember that the theoretical quantities have been calculated under the hypothesis that the dark halo is totally made out by MACHOs, i.e. with f = 1. Actually, the exact value of f is not well known: from the more recent observational constraints it is quite unlikely that f = 1. However to take into account of f is not very difficult: we have simply to multiply by f the expression of the differential rate
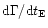 and consequently the ones obtained for
and consequently the ones obtained for
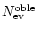 and
and
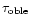 .
Note that
.
Note that
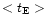 is independent on the value of f.
Then we have the following relations between observable and observed quantities:
is independent on the value of f.
Then we have the following relations between observable and observed quantities:
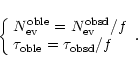 |
(27) |
Dividing these two equations and using the relation
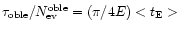 ,
one gets:
,
one gets:
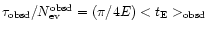 ,
which may be used to test the correctness of our previous estimate of
,
which may be used to test the correctness of our previous estimate of
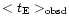 .
For each model, we may solve the system (27) in the unknowns
.
For each model, we may solve the system (27) in the unknowns  and f and estimate them toghether with the errors connected to our analysis. Solving Eqs. (27) is not really useful since the very high error on
and f and estimate them toghether with the errors connected to our analysis. Solving Eqs. (27) is not really useful since the very high error on
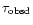 leads us to get no constraints at all on the parameters
leads us to get no constraints at all on the parameters
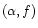 .
We may then use a third relation we have at our disposal, given by
.
We may then use a third relation we have at our disposal, given by
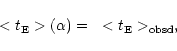 |
(28) |
which is quite easy to solve numerically to get an estimate of the slope 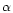 of the MF. Solving Eq. (28), taking into account also the uncertainties, will give us in general more than one solution compatible with the microlensing data. A further selection can be done imposing that
of the MF. Solving Eq. (28), taking into account also the uncertainties, will give us in general more than one solution compatible with the microlensing data. A further selection can be done imposing that 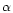 must be in the range
(0.0, 5.0) since values outside this range are reasonably quite unlikely
must be in the range
(0.0, 5.0) since values outside this range are reasonably quite unlikely![[*]](/icons/foot_motif.gif) . In this way, for each model, we have estimated a range
. In this way, for each model, we have estimated a range
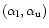 for the slope of the MF simply requiring that
for the slope of the MF simply requiring that
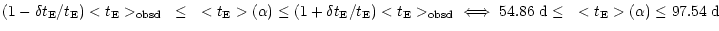 |
|
|
(29) |
being
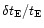 the fractional error on
the fractional error on
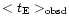 which we have previously estimated to be of order of 28%. These values are summarised in Table 4, where we report also the value of
which we have previously estimated to be of order of 28%. These values are summarised in Table 4, where we report also the value of 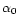 corresponding to the average value
corresponding to the average value
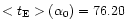 d.
d.
Table 4:
Estimates of the slope 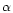 and the dark halo mass fraction f composed by MACHOs for different models labelled as explained before.
and the dark halo mass fraction f composed by MACHOs for different models labelled as explained before.
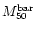 is the mass in MACHOs inside 50 kpc (with
is the mass in MACHOs inside 50 kpc (with
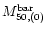 the value corresponding to
the value corresponding to  and f0) measured in units of
and f0) measured in units of
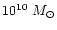 .
Note that the value of
.
Note that the value of
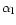 for model B2a differs considerably from the others since the maximum value of
for model B2a differs considerably from the others since the maximum value of
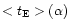 is only 96.2 d, which is lower than the upper limit on the
is only 96.2 d, which is lower than the upper limit on the
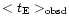 given in Eq. (29).
given in Eq. (29).
| Code |
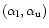 |
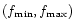 |
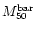 |
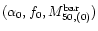 |
| A2a |
(0.50, 1.48) |
(0.12, 0.33) |
4.68 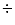 12.87
12.87 |
(1.10, 0.21, 8.19) |
| A2b |
(0.73, 1.50) |
(0.10, 0.30) |
4.02 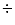 12.06
12.06 |
(1.15, 0.19, 7.63) |
| A2c |
(0.80, 1.50) |
(0.11, 0.32) |
4.63 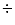 13.47
13.47 |
(1.17, 0.20, 8.42) |
| A2d |
(0.84, 1.56) |
(0.12, 0.35) |
5.18 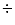 15.12
15.12 |
(1.21, 0.22, 9.50) |
| B2a |
(0.27, 1.69) |
(0.11, 0.33) |
4.29 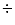 12.87
12.87 |
(1.12, 0.24, 9.36) |
| B2b |
(0.63, 1.80) |
(0.10, 0.30) |
4.02 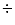 12.06
12.06 |
(1.25, 0.18, 7.24) |
| B2c |
(0.77, 1.89) |
(0.10, 0.32) |
4.21 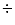 13.47
13.47 |
(1.34, 0.19, 8.00) |
| B2d |
(0.77, 1.90) |
(0.11, 0.34) |
4.75 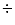 14.79
14.79 |
(1.34, 0.21, 9.07) |
Having estimated 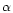 and being
and being
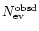 known, we may now get a constraint also on f: on the plot
known, we may now get a constraint also on f: on the plot
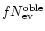 as a function of
as a function of 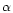 and f we make the contour levels for
and f we make the contour levels for
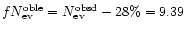 and
and
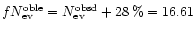 .
On this graph one has to add also the vertical lines corresponding to
.
On this graph one has to add also the vertical lines corresponding to
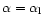 and
and
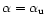 (see Fig. 2). The region
(see Fig. 2). The region  of the parameter space
of the parameter space
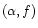 delimited by the two level curves and these two vertical lines is that which is consistent with the constraints on
delimited by the two level curves and these two vertical lines is that which is consistent with the constraints on 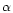 and the ones coming from microlensing observations towards LMC, i.e. the number of observed events and their mean duration. From Fig. 2 one sees that it is possible to define
and the ones coming from microlensing observations towards LMC, i.e. the number of observed events and their mean duration. From Fig. 2 one sees that it is possible to define
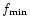 and
and
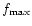 as the minimum and maximum value of f in the region
as the minimum and maximum value of f in the region 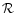 and a value f0 such that
and a value f0 such that
One has then that for each value of
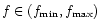 there exists a value of
there exists a value of
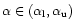 such that
such that
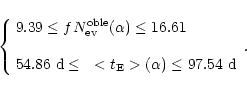 |
(30) |
The values of
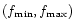 and f0 are summarised in Table 4 for the different models considered
and f0 are summarised in Table 4 for the different models considered![[*]](/icons/foot_motif.gif) . We also give in the same table the range for the mass in MACHOs inside 50 kpc (indicated as
. We also give in the same table the range for the mass in MACHOs inside 50 kpc (indicated as
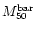 )
which is easily estimated as
)
which is easily estimated as
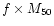 (with M50 given in Table 1) since it is this quantity which is most strongly constrained by microlensing observations.
(with M50 given in Table 1) since it is this quantity which is most strongly constrained by microlensing observations.
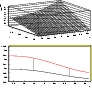 |
Figure 2:
In the upper panel we plot
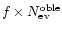 as a function of
as a function of 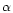 and f; in the lower one, we determine the region
and f; in the lower one, we determine the region 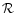 of the parameter space
of the parameter space
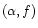 consistent with microlensing observations towards LMC: the upper line in the second panel is the level curve
consistent with microlensing observations towards LMC: the upper line in the second panel is the level curve
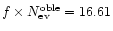 ,
the lower one for ,
the lower one for
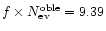 ,
whilst the two dashed lines have been drawn intersecting the level curves with the vertical lines ,
whilst the two dashed lines have been drawn intersecting the level curves with the vertical lines
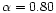 and
and
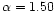 .
The plot is for model A2c; similar plots are obtained for the other models. .
The plot is for model A2c; similar plots are obtained for the other models. |


Up: Constraints on the slope observables
Copyright ESO 2001
![]() of the lens MF and the dark halo mass fraction f composed by MACHOs for each one of the models labelled by the codes previously explained. We consider data coming from the first 5.7 years of observations towards LMC by the MACHO collaboration (Alcock et al. 2000a), limiting ourselves to the thirteen events selected according to the so-called selection criteria A. These are high S/N events and are spatially distributed in a way which is consistent with the hypothesis that they are due to lenses belonging to our halo and not to LMC self lensing; we will discuss of this problem later on. For this set of events we have
of the lens MF and the dark halo mass fraction f composed by MACHOs for each one of the models labelled by the codes previously explained. We consider data coming from the first 5.7 years of observations towards LMC by the MACHO collaboration (Alcock et al. 2000a), limiting ourselves to the thirteen events selected according to the so-called selection criteria A. These are high S/N events and are spatially distributed in a way which is consistent with the hypothesis that they are due to lenses belonging to our halo and not to LMC self lensing; we will discuss of this problem later on. For this set of events we have
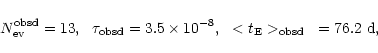
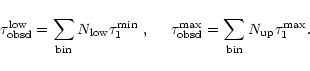
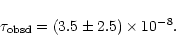
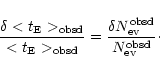
![]() and consequently the ones obtained for
and consequently the ones obtained for
![]() and
and
![]() .
Note that
.
Note that
![]() is independent on the value of f.
Then we have the following relations between observable and observed quantities:
is independent on the value of f.
Then we have the following relations between observable and observed quantities: