We discuss now the problem of the LMC self lensing and show how our results depend quite weakly on the systematics connected with it LMC. As discussed in the introduction, our analysis implicitly assumed that all the observed events are due to lenses belonging to our dark halo. Even if there are different evidencies against a dominant contribution of self lensing, it is still possible that two or three of the 13 events considered are due to LMC self lensing. This means that we have to repeat our analysis excluding from the sample those events which are not caused by MACHOs. Unfortunately, it is not really possible to establish precisely what are these events, due to the well known degeneracy in the lens parameters which does not allow to determine its distance with respect to the observer. However, we may qualitatevely correct our results excluding form the sample some events chosen according to which are more likely to be due to self lensing. To this aim we have used the results on the self lensing events timescale distribution obtained by Gyuk et al. (2000). Their analysis shows that the most likely duration of self lensing events is
![]() d; so we repeated our analysis for different choices of the excluded events. As an example we discuss here the results obtained for the model A2c
d; so we repeated our analysis for different choices of the excluded events. As an example we discuss here the results obtained for the model A2c
![]() ;
similar results are obtained for the other models. As a first test, we have excluded from the sample the events labelled 7, 13 and 14 in Table 7 of Alcock et al. (2000a) which are the longest ones. We have then
;
similar results are obtained for the other models. As a first test, we have excluded from the sample the events labelled 7, 13 and 14 in Table 7 of Alcock et al. (2000a) which are the longest ones. We have then
![]() and
and
![]() ;
the uncertainties on these quantities increase to
;
the uncertainties on these quantities increase to
![]() both on
both on
![]() and on
and on
![]() .
We get
.
We get
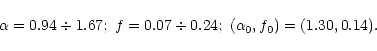
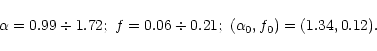
Copyright ESO 2001