

Up: Constraints on the slope observables
In this paper we have analysed a wide class of spheroidal non singular isothermal dark halo models with a homogenous power-law MF by changing the halo flattening q and the lower and upper MACHO mass limits
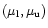 .
Using the simple technique of the inverse problem method we have obtained useful constraints on the slope
.
Using the simple technique of the inverse problem method we have obtained useful constraints on the slope 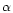 of the MF and the dark halo mass fraction f made out by MACHOs. The results obtained are summarized in Table 4, where we report the estimated ranges for the slope
of the MF and the dark halo mass fraction f made out by MACHOs. The results obtained are summarized in Table 4, where we report the estimated ranges for the slope 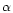 of the lens MF, for the the dark halo mass fraction f made out by MACHOs and for the mass in MACHOs inside 50 kpc. In the same table we also report the values
of the lens MF, for the the dark halo mass fraction f made out by MACHOs and for the mass in MACHOs inside 50 kpc. In the same table we also report the values
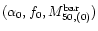 (the latter being the value of
(the latter being the value of
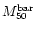 obtained with f = f0) which may be considered as a sort of best fit for each model, since for these values of the parameters the model is consistent with microlensing constraints independently on the estimates of the errors. Having in mind that for each value of
obtained with f = f0) which may be considered as a sort of best fit for each model, since for these values of the parameters the model is consistent with microlensing constraints independently on the estimates of the errors. Having in mind that for each value of
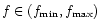 there exists only one value of
there exists only one value of
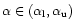 such that the model with these values of
such that the model with these values of
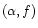 satisfies the constraints (30), we may draw some interesting considerations from Table 4.
satisfies the constraints (30), we may draw some interesting considerations from Table 4.
- 1.
- The first striking feature in Table 4 is that there are no models with
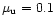 (models A1 and B1 in our notation). This happens because the constraint (29) on
(models A1 and B1 in our notation). This happens because the constraint (29) on
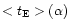 for these models gives values of
for these models gives values of 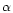 outside the range
(0.0, 5.0). Thus we may conclude that non singular isothermal spheroidal models filled with MACHOs of mass less than
outside the range
(0.0, 5.0). Thus we may conclude that non singular isothermal spheroidal models filled with MACHOs of mass less than
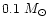 are not consistent with microlensing observations towards LMC. Thus there exist MACHOs with mass greater than the hydrogen burning limit (
are not consistent with microlensing observations towards LMC. Thus there exist MACHOs with mass greater than the hydrogen burning limit (
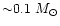 ); such interpretation is consistent with MACHO and EROS result on the most likely MACHO mass (
); such interpretation is consistent with MACHO and EROS result on the most likely MACHO mass (
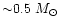 )
and will have important implications on the question of their nature. Actually, if MACHOs weigth more than
)
and will have important implications on the question of their nature. Actually, if MACHOs weigth more than
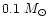 ,
then they should be unusual baryonic objects (e.g. very old white dwarfs) or non baryonic at all (Sazhin et al. 1996; Gurevich et al. 1997). However, data are too few to conclude that this interpretation is correct. We have examined spheroidal non singular isothermal density models, but it is still possible that the halo mass density has a different radial profile with a non flat rotation curve (see, e.g., Wilkinson & Evans 1999) which deserve some attention.
,
then they should be unusual baryonic objects (e.g. very old white dwarfs) or non baryonic at all (Sazhin et al. 1996; Gurevich et al. 1997). However, data are too few to conclude that this interpretation is correct. We have examined spheroidal non singular isothermal density models, but it is still possible that the halo mass density has a different radial profile with a non flat rotation curve (see, e.g., Wilkinson & Evans 1999) which deserve some attention.
- 2.
- The estimated ranges for
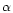 do overlap both for models with the same halo flattening q but different mass limits
do overlap both for models with the same halo flattening q but different mass limits
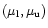 and for models with the same mass limits but different halo flattening. This is encouraging since it means that our estimates do not depend on the halo flattening which is poorly constrained. Considering the whole set of models in Table 4, an estimate of
and for models with the same mass limits but different halo flattening. This is encouraging since it means that our estimates do not depend on the halo flattening which is poorly constrained. Considering the whole set of models in Table 4, an estimate of 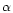 can be given in the range
can be given in the range
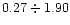 ,
which practically is the widest range of variability. Unfortunately it is not a narrow range because of the high errors connected to the low statistics.
,
which practically is the widest range of variability. Unfortunately it is not a narrow range because of the high errors connected to the low statistics.
It is not very easy to compare this estimate with other results, since the present state of the studies on the dark halo MF is still in progress (Merá et al. 1998). Collecting together results on the nearby halo LF, based on geometric parallax determinations of high velocity faint stars in the solar neighbourhood, and those about the spheroid MF, Chabrier & Méra estimate that the halo MF is a power-law with
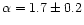 (Chabrier & Méra 1997). We can see from Table 4 that the range for
(Chabrier & Méra 1997). We can see from Table 4 that the range for 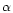 obtained for the B2 models, that is for
obtained for the B2 models, that is for
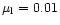 and
and
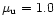 ,
are consistent with the value obtained by Chabrier & Méra (1997).This means to put a constrain on the low mass objects of the dark halo. Another important indication on the halo MF comes from studies of the stellar populations of the globular clusters. The MFs of different clusters observed with the HST have been determined recently by Chabrier & Méra (1997) who found that they are weakly dependent on the metallicity and may be modelled as power-law with slope
,
are consistent with the value obtained by Chabrier & Méra (1997).This means to put a constrain on the low mass objects of the dark halo. Another important indication on the halo MF comes from studies of the stellar populations of the globular clusters. The MFs of different clusters observed with the HST have been determined recently by Chabrier & Méra (1997) who found that they are weakly dependent on the metallicity and may be modelled as power-law with slope
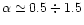 till 0.1
till 0.1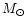 .
With this range for
.
With this range for 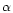 also the A2 models are consistent. Note that we have also consistency with MACHO results.
also the A2 models are consistent. Note that we have also consistency with MACHO results.
- 3.
- The estimated ranges for f are consistent with the recent estimate obtained by MACHO (Alcock et al. 2000a) using a maximum likelihood method and a different set of halo models. The best fit values f0 are constrained in a very narrow range: from 0.19 to 0.24; the analysis of Table 4 shows that the total range for f is quite narrow as well: from 0.10 to 0.35. This shows that it is not possible to increase the dark halo mass fraction flattening the dark halo. The same agreement with MACHO results is found with respect to the baryonic mass inside 50 kpc (
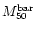 in Table 4). Our estimates range from 4.02 to
in Table 4). Our estimates range from 4.02 to
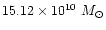 whilst MACHO estimates range from 6 to
whilst MACHO estimates range from 6 to
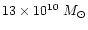 .
Also the best fit values are in good agreement. These are encouraging results and lead us to be quite confident in our analysis. Once again, one should also consider different radial profiles for the mass density before drawing some definitive conclusion.
.
Also the best fit values are in good agreement. These are encouraging results and lead us to be quite confident in our analysis. Once again, one should also consider different radial profiles for the mass density before drawing some definitive conclusion.
Although not definitely conclusive, we obtained constrains on the dark halo parameters on the basis of microlensing observations for a wide class of spheroidal non singular isothermal models. We performed our analysis on the basis of the microlensing data only in one direction, the LMC, and in fact it has been not possible to determine uniquely the properties of the models we considered. In order to investigate the shape of the halo and put more precise constraints on the relative parameters, it will be necessary to have microlensing data relative to observations towards other directions, for example towards globular clusters; they may be used as sources (Gyuk & Holder 1997) or as sites of lenses when observing towards SMC (Jetzer et al. 1998). There are also other possible targets such as spiral arms (Grenacher et al. 1999) which could be investigated. It would be also interesting to compare microlensing results on galactic models parameters with the ones obtained from the rotation curves of other spiral galaxies similar to our Milky Way, in particular those deduced from the universal rotation curve proposed by Persic et al. (1996) upon their analysis of a large homogenous sample of spiral galaxies. All that constitutes material for further work.
Acknowledgements
It is a great pleasure to thank the SLOTT group of Napoli (G. Covone, E. Piedipalumbo, C. Rubano, P. Scudellaro and M. Sereno) and Salerno (V. Bozza, S. Calchi Novati, S. Capozziello, G. Iovane, G. Lambiase, V. Re and G. Scarpetta) and Ph. Jetzer and L. Grenacher for the discussions we had on the manuscript. We also thank the anonymous referee for the usefull comments which have helped to improve the paper.


Up: Constraints on the slope observables
Copyright ESO 2001
![]() .
Using the simple technique of the inverse problem method we have obtained useful constraints on the slope
.
Using the simple technique of the inverse problem method we have obtained useful constraints on the slope ![]() of the MF and the dark halo mass fraction f made out by MACHOs. The results obtained are summarized in Table 4, where we report the estimated ranges for the slope
of the MF and the dark halo mass fraction f made out by MACHOs. The results obtained are summarized in Table 4, where we report the estimated ranges for the slope ![]() of the lens MF, for the the dark halo mass fraction f made out by MACHOs and for the mass in MACHOs inside 50 kpc. In the same table we also report the values
of the lens MF, for the the dark halo mass fraction f made out by MACHOs and for the mass in MACHOs inside 50 kpc. In the same table we also report the values
![]() (the latter being the value of
(the latter being the value of
![]() obtained with f = f0) which may be considered as a sort of best fit for each model, since for these values of the parameters the model is consistent with microlensing constraints independently on the estimates of the errors. Having in mind that for each value of
obtained with f = f0) which may be considered as a sort of best fit for each model, since for these values of the parameters the model is consistent with microlensing constraints independently on the estimates of the errors. Having in mind that for each value of
![]() there exists only one value of
there exists only one value of
![]() such that the model with these values of
such that the model with these values of
![]() satisfies the constraints (30), we may draw some interesting considerations from Table 4.
satisfies the constraints (30), we may draw some interesting considerations from Table 4.
![]() (Chabrier & Méra 1997). We can see from Table 4 that the range for
(Chabrier & Méra 1997). We can see from Table 4 that the range for ![]() obtained for the B2 models, that is for
obtained for the B2 models, that is for
![]() and
and
![]() ,
are consistent with the value obtained by Chabrier & Méra (1997).This means to put a constrain on the low mass objects of the dark halo. Another important indication on the halo MF comes from studies of the stellar populations of the globular clusters. The MFs of different clusters observed with the HST have been determined recently by Chabrier & Méra (1997) who found that they are weakly dependent on the metallicity and may be modelled as power-law with slope
,
are consistent with the value obtained by Chabrier & Méra (1997).This means to put a constrain on the low mass objects of the dark halo. Another important indication on the halo MF comes from studies of the stellar populations of the globular clusters. The MFs of different clusters observed with the HST have been determined recently by Chabrier & Méra (1997) who found that they are weakly dependent on the metallicity and may be modelled as power-law with slope
![]() till 0.1
till 0.1![]() .
With this range for
.
With this range for ![]() also the A2 models are consistent. Note that we have also consistency with MACHO results.
also the A2 models are consistent. Note that we have also consistency with MACHO results.