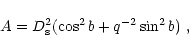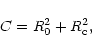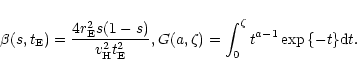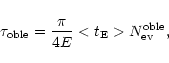Up: Constraints on the slope observables
To apply the method, as we have outlined in the introduction, we have first to calculate the observable quantities in microlensing to which we will compare the observed ones towards LMC. These quantities are the number of events, the observable optical depth and the mean duration. In all this calculation, we will take into account the detection efficiency in order to be sure that the comparison between predicted and observed quantities is meaningful.
The starting point is the general expression of the differential rate (De Rujula et al. 1991)
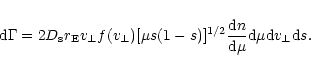 |
(5) |
In Eq. (5),
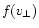 is the transverse velocity distribution and
is the transverse velocity distribution and
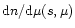 is the halo lens MF; in the reasonable hypothesis of homogeneity, this latter may be factorized as:
is the halo lens MF; in the reasonable hypothesis of homogeneity, this latter may be factorized as:
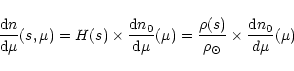 |
(6) |
being
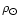 the local mass density of the model and
the local mass density of the model and
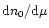 the local MF. Changing variable from
the local MF. Changing variable from 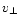 to
to 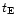 and integrating we get
and integrating we get
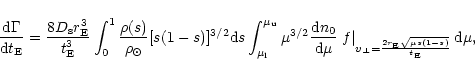 |
(7) |
being
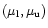 the lower and upper limit for the mass of MACHOs. From Eq. (7) one immediately see that to go on further we need to assign the transverse velocity distribution, the local MF and the mass density of the halo model.
the lower and upper limit for the mass of MACHOs. From Eq. (7) one immediately see that to go on further we need to assign the transverse velocity distribution, the local MF and the mass density of the halo model.
Since we do not consider anisotropy in the velocity space, we may assume the following maxwellian distribution of the transverse velocities
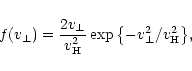 |
(8) |
where 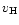 is the velocity dispersion which we fix as 210 km s-1.
is the velocity dispersion which we fix as 210 km s-1.
With regard to the local MF, it is usual to assume that all the MACHOs have the same mass which means that
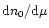 is a
is a 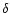 -Dirac centered on the common mass. This is just a first approximation: it is worthwhile to explore different possibilities. As a generalization we consider the case of a homogenous power-law MF for the MACHOs, i.e. we assume
-Dirac centered on the common mass. This is just a first approximation: it is worthwhile to explore different possibilities. As a generalization we consider the case of a homogenous power-law MF for the MACHOs, i.e. we assume
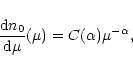 |
(9) |
being 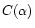 a normalization constant fixed such that
a normalization constant fixed such that
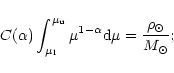 |
(10) |
this gives:
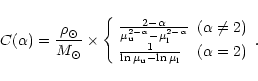 |
(11) |
Concerning the mass density of the dark halo we will restrict our analysis to a class of spheroidal non singular isothermal models whose density distribution is given by
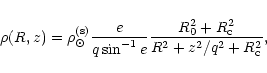 |
(12) |
where
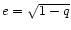 with q the halo flattening,
with q the halo flattening,
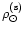 is the local mass density
is the local mass density![[*]](/icons/foot_motif.gif) for the spherical case, R0 is the galactocentric distance of the Sun and
for the spherical case, R0 is the galactocentric distance of the Sun and 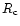 is the core radius.
is the core radius.
Inserting now Eqs. (8), (9) and (12) into Eq. (7) and expressing (R,z) in terms of (s, l, b) (with (l,b) galactic angular coordinates of the target), we finally get
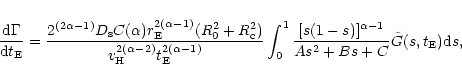 |
(13) |
being
and we have defined for sake of shortness
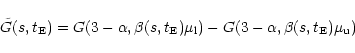 |
(14) |
with
Given
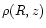 it is quite straightforward to get all the observable quantities we need in the following. The first one is the number of observable events, which is simply given by
it is quite straightforward to get all the observable quantities we need in the following. The first one is the number of observable events, which is simply given by
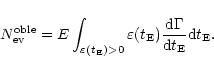 |
(15) |
Introducing the expression given by (13) into Eq. (15) one gets
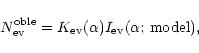 |
(16) |
having posed
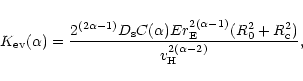 |
(17) |
![\begin{displaymath}%
I_{\rm ev}(\alpha;\, {\rm model}) = \int_{\varepsilon(t_{\r...
...s)]^{\alpha -1}}{As^2+Bs+C} \tilde{G}(s,t_{\rm E}) {\rm d}s} .
\end{displaymath}](/articles/aa/full/2001/29/aah2555/img78.gif) |
(18) |
Also, from Eq. (13) and definition (3), we get the following expression for the observable optical depth:
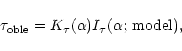 |
(19) |
being now
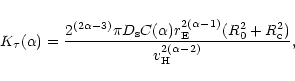 |
(20) |
![\begin{displaymath}%
I_{\tau}(\alpha; {\rm model}) = \int_{\varepsilon(t_{\rm E}...
...s)]^{\alpha -1}}{As^2+Bs+C} \tilde{G}(s,t_{\rm E}) {\rm d}s} .
\end{displaymath}](/articles/aa/full/2001/29/aah2555/img81.gif) |
(21) |
Now it is not difficult to get the predicted mean duration; in order to take into account the detection efficiency, we define this quantity as
 |
(22) |
This definition is nothing else but a straightforward generalization of the usual one (Jetzer 1998) to which it reduces in the case of perfect detection efficiency, i.e. when
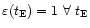 .
It is not surprising, then, that the following relation holds:
.
It is not surprising, then, that the following relation holds:
which is immediately demonstrated. Using such a relation and Eqs. (16) and (19), we finally get
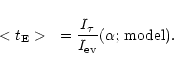 |
(23) |
In Eqs. (16), (19) and (23) we have indicated the unknown parameters which these quantities depend on. These are essentially the slope 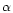 of the MF and the parameters needed to specify the characteristics of the halo model. We have decided to not consider the mass limits as unknown parameters, although they are not very well constrained. In fact, in the following analysis we retain as fixed these two quantities and investigate the dependence on the remaining unknowns.
of the MF and the parameters needed to specify the characteristics of the halo model. We have decided to not consider the mass limits as unknown parameters, although they are not very well constrained. In fact, in the following analysis we retain as fixed these two quantities and investigate the dependence on the remaining unknowns.


Up: Constraints on the slope observables
Copyright ESO 2001
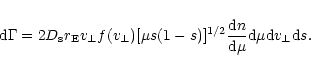
![]() is a
is a ![]() -Dirac centered on the common mass. This is just a first approximation: it is worthwhile to explore different possibilities. As a generalization we consider the case of a homogenous power-law MF for the MACHOs, i.e. we assume
-Dirac centered on the common mass. This is just a first approximation: it is worthwhile to explore different possibilities. As a generalization we consider the case of a homogenous power-law MF for the MACHOs, i.e. we assume