1 Introduction

The usefulness of gravitational microlensing as a tool to investigate the structure of the galactic dark halo is now firmly established. Since Paczynski's seminal paper (Paczynski 1986), several collaborations have searched for microlensing events towards LMC (Renault et al. 1997; Alcock et al. 2000a), SMC (Alcock et al. 1997c; Afonso et al. 1999) and M31 (Ansari et al. 1997). While the presence of MACHOs (Massive Astrophysical Compact Halo Objects) has been witnessed by the microlensing events already found, many questions about their nature and the structure of the dark halo are still open.

One of the main quantities that characterises the microlensing properties of a particular MACHO population is the optical depth $\tau$. This quantity is simply the number of lenses inside the microlensing tube, a cylinder whose axis is the line of sight to the source and with radius equal to the Einstein radius, defined as (Mollerach & Roulet 1997)

$$R_{\rm E} = \sqrt{\frac{4Gm}{c^2} \frac{D_{\rm d} (D_{\rm s} - D_{\rm d})}{D_{\rm s}}} = r_{\rm E} \sqrt{\mu s(1-s)} \ ,$$

where m is the mass of the lens (with $\mu = m/M_{\odot}$), $D_{\rm s}$ ($D_{\rm d}$) the distance to the source (the lens), $s=D_{\rm d}/D_{\rm s}$ and we have posed $r_{\rm E} = \sqrt{4GM_{\odot} D_{\rm s}/c^2}$. In its simplest form, $\tau$ is defined as (Paczynski 1986; Mollerach & Roulet 1997; Jetzer 1998)

$$% \tau = \int_0^1{\frac{\pi R_{\rm E}^2}{m} \rho (s) {\rm d}s... ...c{4\pi G D_{\rm s}^2}{c^2}\int_0^1{\rho (s) s (1-s) {\rm d}s},$$ (1)

having supposed (as usually) that the halo extends till the source, while $\rho(s)$ is the MACHOs mass density. Optical depth is obtained from observations using the formula (Alcock et al. 1997b)

$$% \tau_{\rm meas} = \frac{\pi}{4E} \sum_i \frac{t_{{\rm E},i}}{\varepsilon(t_{{\rm E},i})} ,$$ (2)

being E the total exposure in star-years (which is simply the number of monitored object multiplied by the total period of observations), $t_{\rm E} = 2R_{\rm E}/v_{\perp}$ the Einstein diameter crossing time (with $v_{\perp}$ the MACHO' s velocity transverse to the line of sight), $\varepsilon(t_{{\rm E},i})$ the detection efficiency for the ith event and the sum is over the observed events.

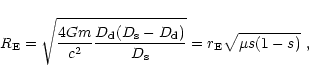
Having estimated $\tau_{\rm meas}$ from observations with Eq. (2) and calculated the predicted optical depth for an assumed model of full MACHO halo from Eq. (1), an easy way to evaluate the halo mass fraction composed by MACHOs is to compute the ratio between these two quantities to get $f = \tau_{\rm meas}/\tau$. However, Alcock et al. (1997a) have pointed out that Eq. (2) is not a measure of the total optical depth, but only of the optical depth of events which fall in the range of timescales for which $\varepsilon(t_{\rm E}) > 0$. Following this remark, Kerins (1998) has introduced the concept of observable optical depth defining it as

$$% \tau_{\rm oble} = \frac{\pi}{4} \int_{\varepsilon(t_{\rm E}... ... E} \frac{{\rm d}\Gamma}{{\rm d}t_{\rm E}} {\rm d}t_{\rm E}} ,$$ (3)

where ${\rm d}\Gamma/{\rm d}t_{\rm E}$ is the differential rate for the assumed halo model, being the rate $\Gamma$ the number of events per unit time (Mollerach & Roulet 1997; Jetzer 1998). Then, the halo mass fraction f is more correctly estimated as $\tau_{\rm obsd}/\tau_{\rm oble}$, being $\tau_{\rm obsd}$ the directly observed optical depth, i.e. (Kerins 1998)

$$% \tau_{\rm obsd} = \frac{\pi}{4E} \sum_i t_{{\rm E},i} .$$ (4)

Using these quantities, Kerins has shown that the comparison between observed and obervable optical depths may give only a lower limit on f, while no upper limit may be obtained without a knowledge of the full distribution function of the halo model and of the MACHO's mass function (hereafter MF), i.e. the number density of MACHOs with mass in the range $(\mu, \mu + {\rm d}\mu)$. The result obtained by Kerins was proved under the hypothesis that all the lenses have the same mass and assuming a standard cored isothermal sphere for the dark halo mass density. In this paper we generalize the calculation of $\tau_{\rm oble}$ and analyze a general class of homogenous MF. Several studies have been made by many authors to determine the MF function by microlensing data, but they are essentially devoted to the MF of bulge lenses (Zhao et al. 1995; Han & Gould 1996; Grenacher et al. 1999) and the work is still in progress. Mao & Paczynski (1996) considered simplified toy models and a power-law MF and estimated that a reliable determination could be achieved only if we had 100 or more events. Their results, obtained under the assumption that MACHO's spatial distribution and kinematics were known, have been confirmed by Markovic & Sommer-Larsen (1997) who have also studied the effect of changing halo model on the estimated average mass of lensing objects. All these studies are based on statistical methods, that is why there is need of a large number of events to reduce the error on parameters determination. In this paper we use a different technique to get useful informations on the lensing objects MF. Since microlensing observable quantities, i.e. number of events, observable optical depth and mean duration, depend on the dark halo model and on the MF, we may express these quantities as functions of some models parameters and of the slope of the MF itself. Then a comparison between theoretical expectations and observed quantities will help us to recover the values of the model's parameters simply imposing that theory and observations are in good agreement. This is what we call the inverse problem in microlensing. To be meaningful our analysis must take into account also the detection efficiency and that is why our theoretical expectations have to be corrected for this effect too. In the following we will show how this is possible and will get some interesting constraints on the dark halo mass fraction f composed by MACHOs and the slope $\alpha$ of the assumed homogenous power-law MF for a wide class of spheroidal models. By the way our method is not able to escape the problems connected to the low number of observed events and actually our results are strongly affected by errors which do not allow us to constrain the slope $\alpha$ of the MF in a narrow range. Were the errors be reduced by increasing the number of observed events, our method should be able to narrow the uncertainties on the MACHOs MF.

There is one possible source of systematic error connected to our analysis. In the previous discussion, we have implicitly assumed that all the observed events are due to MACHOs in the Milky Way dark halo, but it should be considered also the possibility that at least part of the events are due to LMC self lensing. This hypothesis has been suggested in many papers, but the recent analysis by the MACHO group of the spatial distribution of the events across the observed LMC fields has shown that this latter is not compatible with the proposed models of self lensing. As a further test, MACHO has also analyzed the CMD (Color Magnitude Diagram) of the sources of their first eight events to see if they reside in the LMC disk or behind it. Even if the sample is too small to get a definitive result, the hypothesis that all the eight events are due to halo lenses is slightly favoured (Alcock et al. 2000b). However, there is still the possibility that there are no MACHOs at all in the dark halo and that the observed events are due to the LMC dark halo. In fact, the maximum likelihood analysis of the MACHO collaboration has shown that this hypothesis is not completely excluded, even if the needed LMC model should be somewhat extreme. Besides, a recent paper by Alves & Nelson (2000) has shown that the LMC rotation curve and the data on the kinematics of the carbon stars in LMC are best fitted by a model composed by a flared and warped disk and no dark halo. If this result will be confirmed by future works, it will strenghten our assumption that the observed microlensing events are due to MACHOs in Milky Way dark halo. In the meantime, we are constrained to consider the effects that a possible contamination by self lensing should have on our results. We will discuss how this will affect our results presenting some qualitative tests.

In Sect. 2 we introduce and evaluate the microlensing observables, i.e. the number of events, the observable optical depth and the mean duration, taking into account the detection efficiency for models with isotropic Maxwellian transverse velocity distribution and homogenous power-law MF and assuming a wide class of spheroidal non singular isothermal models. The model parameters and the way we fix some of them is detailed in Sect. 3 where we illustrate the models we have chosen to explore. Section 4 is devoted to the analysis of the different models with the simple technique of the inverse problem method to get constraints on the slope of the lens MF and the dark halo mass fraction composed by MACHOs. How the self lensing could affect our results is discussed qualitatively in Sect. 5, while a final discussion of the results is presented in the conclusions.