![$\displaystyle \sum_{j}\frac{1}{u_j I_j^{2}}\left[A_jU_j{+}
B_j U_j^{2} {+}C_j \,\ln(u_j)+D_j\frac{\ln(u_j)}{u_j}\right]$](/articles/aa/full/2001/27/aa1246/img157.gif) |
(A.1) |
For the direct ionization (DI) cross sections we chose the fitting
formula proposed by Arnaud & Rothenflug (1985) from the
work of Younger (1981):
The parameters Aj, Bj, Cj, Dj (in units of 10-14cm2eV2) and Ij (in eV) are taken from the works of Arnaud & Raymond (1992) for iron, and of Arnaud & Rothenflug (1985) for the others elements. The parameters for elements not considered in these works are given in Mazzotta et al. (1998).
For a Maxwellian electron distribution, Arnaud & Rothenflug
(1985) obtained according to Eqs. (2),
(8) and (A.1), the rate:
| (A.3) |
Similar to the Hybrid electron distribution, the direct ionization
rate
![]() is given by:
is given by:
![]() is the sum of the
contribution of the truncated Maxwellian component and the power-law
component:
is the sum of the
contribution of the truncated Maxwellian component and the power-law
component:
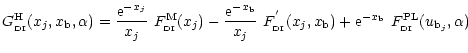 |
(A.6) |
| = | (A.7) | ||
| = | ![$\displaystyle A_j \left[1-x_j f_{1}(x_{\rm b})\right]+B_j \left[1+\frac{x_j}{u_{{\rm b}_{j}}}-x_j (2+x_j) f_1(x_{\rm b})\right]$](/articles/aa/full/2001/27/aa1246/img172.gif) |
||
| (A.8) | |||
| = | ![$\displaystyle A_{j}\left[ \frac{u_{{\rm b}_{j}}}{\alpha-1/2} -
\frac{1}{\alpha+...
.../2} {-} \frac{2}{\alpha+1/2} {+}\frac{u_{{\rm b}_{j}}^{-1}}{\alpha+3/2} \right]$](/articles/aa/full/2001/27/aa1246/img175.gif) |
||
![$\displaystyle +\frac {C_j u_{{\rm b}_{j}}}{\alpha-1/2} \left[ \ln(u_{{\rm b}_{j...
...{D_j}{\alpha+1/2} \left[\ln(u_{{\rm b}_{j}}) + \frac{1}{\alpha+1/2}\right]\cdot$](/articles/aa/full/2001/27/aa1246/img176.gif) |
(A.9) |
Only the power-law component contributes of the electron distribution
to the rate:
| (A.11) |
For the excitation autoionization (EA) cross sections, we
used the generalized formula proposed by Arnaud & Raymond
(1992):
The parameters A, B, C, D, E (in units of
10-16cm2eV) and
![]() (in eV) are taken from the works
of Arnaud & Rothenflug (1985) and Arnaud & Raymond
(1992). The parameters for elements not considered in
these works are given in Mazzotta et al. (1998).
(in eV) are taken from the works
of Arnaud & Rothenflug (1985) and Arnaud & Raymond
(1992). The parameters for elements not considered in
these works are given in Mazzotta et al. (1998).
For the Hybrid electron distribution, the excitation autoionization
rate
![]() is given by:
is given by:
![]() is the sum of the
contribution of the truncated Maxwellian component and the power-law
component:
is the sum of the
contribution of the truncated Maxwellian component and the power-law
component:
| (A.17) |
| = | (A.18) | ||
| = | ![$\displaystyle A+B\left[1-x_{\rm _{\rm EA}}~f_1(x_{\rm b})\right]+C\left[1-\frac{x_{\rm _{\rm EA}}}{u_{\rm _{\rm EA}}}+x_{\rm _{\rm EA}}^{2}~f_1(x_{\rm b})\right]$](/articles/aa/full/2001/27/aa1246/img201.gif) |
(A.19) | |
![$\displaystyle +D\left[1{-}\frac{x_{\rm _{\rm EA}}}{2 u_{\rm _{\rm EA}}^{2}}{+}
...
...}{2}~f_1(x_{\rm b})\right]+E\left[ \ln(u_{\rm _{\rm EA}})+f_1(x_{\rm b})\right]$](/articles/aa/full/2001/27/aa1246/img202.gif) |
|||
| = | ![$\displaystyle A\left[\frac{1}{\alpha-1/2}\right]+B\left[\frac{1}{\alpha-1/2} - ...
...+C\left[\frac{1}{\alpha-1/2} - \frac{u_{\rm _{\rm EA}}^{-2}}{\alpha+3/2}\right]$](/articles/aa/full/2001/27/aa1246/img204.gif) |
(A.20) | |
![$\displaystyle +D\left[\frac{1}{\alpha-1/2} - \frac{u_{\rm _{\rm EA}}^{-3}}{\alp...
...\frac{1}{(\alpha-1/2)^2} +\frac{\ln(u_{\rm _{\rm EA}})}{\alpha-1/2}\right]\cdot$](/articles/aa/full/2001/27/aa1246/img205.gif) |
Only the power-law component contributes of
the electron distribution
to the rate:
| = | 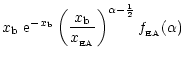 |
(A.21) |
| (A.22) |
The total ionization rate
![]() is obtained by:
is obtained by:
| = | (A.23) |
Copyright ESO 2001