Let us consider a collisional process of cross section ![]() ,
varying with energy E of the incident electron. The corresponding
rate coefficient (cm3s-1), either for a Maxwellian distribution or a Hybrid
distribution, f(x), is given by:
,
varying with energy E of the incident electron. The corresponding
rate coefficient (cm3s-1), either for a Maxwellian distribution or a Hybrid
distribution, f(x), is given by:
The rates for the Hybrid distribution depend on kT, ![]() and
and ![]() and are noted
and are noted
![]() ,
,
![]() and
and
![]() for the ionization, radiative
and dielectronic recombination process respectively. The
corresponding rates for the Maxwellian distribution which only depends
on kT are
for the ionization, radiative
and dielectronic recombination process respectively. The
corresponding rates for the Maxwellian distribution which only depends
on kT are
![]() ,
,
![]() and
and
![]() .
.
The ionization data are taken from Arnaud & Rothenflug (1985) and Arnaud & Raymond (1992), as adopted by Mazzotta et al. (1998) for the most abundant elements considered here. The recombination data are taken from the updated calculations of Mazzotta (1998). In the next sections we outline the general behavior of the rates with the electron distribution parameters, using mostly oxygen ions (but also iron) as illustration.
The ionization cross sections present a threshold at the first
ionization potential of the ionizing ion,
![]() .
The cross
sections always present a maximum, at
.
The cross
sections always present a maximum, at ![]() ,
and decrease as
,
and decrease as
![]() at very high energies (e.g., Tawara et al. 1985).
The ionization rate is very sensitive to the proportion of electrons
above the threshold and the modification of the ionization rate for the
Hybrid distribution depends on how the high energy tail affects this
proportion.
at very high energies (e.g., Tawara et al. 1985).
The ionization rate is very sensitive to the proportion of electrons
above the threshold and the modification of the ionization rate for the
Hybrid distribution depends on how the high energy tail affects this
proportion.
Parametric formulae for the ionization cross sections are available from the litterature and it is easy to derive the corresponding rates for the Hybrid distribution. This is detailed in Appendix A.
To understand the influence of the presence of a high energy power-law
tail in the electron distribution, we computed the ratio
![]() ,
of the ionization rate in a Hybrid distribution over
that in a Maxwellian with the same temperature. This ratio is plotted
in Figs. 3 to 7 for
different ions and values of the parameters
,
of the ionization rate in a Hybrid distribution over
that in a Maxwellian with the same temperature. This ratio is plotted
in Figs. 3 to 7 for
different ions and values of the parameters ![]() and
and ![]() .
.
Let us first consider O+6. Its ionization potential is
![]() and the cross section is maximum at about
and the cross section is maximum at about
![]() .
Its abundance, for a Maxwellian electron distribution, is maximum
at
.
Its abundance, for a Maxwellian electron distribution, is maximum
at
![]() K under ionization equilibrium (Arnaud & Rothenflug
1985). At this temperature, the threshold energy is well above
the thermal energy (
K under ionization equilibrium (Arnaud & Rothenflug
1985). At this temperature, the threshold energy is well above
the thermal energy (
![]() )
and only the very high
energy tail of the Maxwellian contributes to
)
and only the very high
energy tail of the Maxwellian contributes to
![]() ,
i.e. a small
fraction of the electron distribution. This fraction is dramatically
increased in the Hybrid distribution as soon at the break energy is
not too far off from the threshold,
,
i.e. a small
fraction of the electron distribution. This fraction is dramatically
increased in the Hybrid distribution as soon at the break energy is
not too far off from the threshold,
![]() for O+6(Fig. 3). The enhancement factor
for O+6(Fig. 3). The enhancement factor
![]() naturally
increases with decreasing break
naturally
increases with decreasing break ![]() and slope
and slope ![]() parameters
(Fig. 3), since the distribution median energy
increases when these parameters are decreased (Fig. 2).
parameters
(Fig. 3), since the distribution median energy
increases when these parameters are decreased (Fig. 2).
This behavior versus ![]() and
and ![]() is general at all temperatures as
illustrated in Fig. 4, provided that the thermal
energy is not too close to
is general at all temperatures as
illustrated in Fig. 4, provided that the thermal
energy is not too close to ![]() ,
i.e. that the majority of the
contribution to the ionization rate is from electrons with energies
corresponding to the increasing part of the ionization cross section.
If this is no more the case, the ionization rate starts to decrease
with increasing distribution median energy. Thus, for high enough
values of the temperature (see the curve at
T = 108 K in
Fig. 4), the factor
,
i.e. that the majority of the
contribution to the ionization rate is from electrons with energies
corresponding to the increasing part of the ionization cross section.
If this is no more the case, the ionization rate starts to decrease
with increasing distribution median energy. Thus, for high enough
values of the temperature (see the curve at
T = 108 K in
Fig. 4), the factor
![]() becomes less than unity
and decreases with decreasing
becomes less than unity
and decreases with decreasing ![]() .
The correction factor is small
(around
.
The correction factor is small
(around
![]() )
however in that case.
)
however in that case.
![\begin{figure}
\par\includegraphics[width=6.8cm,clip]{MS1246f4.eps}\end{figure}](/articles/aa/full/2001/27/aa1246/Timg83.gif) |
Figure 4:
Same as Fig. 3 but the parameter |
More generally the enhancement factor
![]() at fixed values of
at fixed values of ![]() and
and ![]() ,
depends on the temperature (Fig. 4). It
decreases with increasing temperature: the peak of the distribution is
shifted to higher energy as the ratio
,
depends on the temperature (Fig. 4). It
decreases with increasing temperature: the peak of the distribution is
shifted to higher energy as the ratio
![]() increases and
the enhancement due to the contribution of the hard energy tail
decreases.
increases and
the enhancement due to the contribution of the hard energy tail
decreases.
The qualitative behavior outlined above does not depend on the ion
considered. We plotted in Figs. 5 and 6 the enhancement factor for the different
ions of oxygen and a choice of iron ions at T* (the temperature
of maximum ionization fraction of the ion for a Maxwellian electron
distribution under ionization equilibrium).
![]() is always greater
than unity and the ionization rates are increased by the Hybrid
distribution, the enhancement factor
is always greater
than unity and the ionization rates are increased by the Hybrid
distribution, the enhancement factor
![]() increasing with decreasing
increasing with decreasing
![]() .
However this enhancement factor differs from ion to ion, it
generally increases with increasing
.
However this enhancement factor differs from ion to ion, it
generally increases with increasing
![]() value (approximatively
with an exponential dependence), as shown in
Fig. 7. This is again due to the relative
position of the peak of the distribution with respect to the threshold
energy. Note that
value (approximatively
with an exponential dependence), as shown in
Fig. 7. This is again due to the relative
position of the peak of the distribution with respect to the threshold
energy. Note that
![]() is generally smaller for more
ionized ions (but this is not strictly true) so that low charge
species are generally more affected by the Hybrid distribution.
is generally smaller for more
ionized ions (but this is not strictly true) so that low charge
species are generally more affected by the Hybrid distribution.
In summary, the Hybrid rates are increased with respect to the
Maxwellian rates except at very high temperature. The enhancement
factor depends on the temperature, mostly via the factor
![]() .
It increases dramatically with decreasing temperature and is always
important at T*, where it can reach several orders of magnitude.
The ionization balance is thus likely to be affected significantly,
whereas the effect should be smaller in ionizing plasmas but
important in recombining plasmas.
For
.
It increases dramatically with decreasing temperature and is always
important at T*, where it can reach several orders of magnitude.
The ionization balance is thus likely to be affected significantly,
whereas the effect should be smaller in ionizing plasmas but
important in recombining plasmas.
For ![]() typically lower than 10-20 (with this upper limit higher for lower temperature, see Fig. 4), the impact of the Hybrid rate increases with decreasing
typically lower than 10-20 (with this upper limit higher for lower temperature, see Fig. 4), the impact of the Hybrid rate increases with decreasing ![]() and
and ![]() .
.
![\begin{figure}
\par\includegraphics[width=6.8cm,clip]{MS1246f5.eps} \end{figure}](/articles/aa/full/2001/27/aa1246/Timg86.gif) |
Figure 5:
Same as Fig. 3 for the different ions of oxygen.
Each curve is labeled by the charge of the ion considered. The slope
parameter is fixed to |
The ionization rates for a Hybrid distribution are less dependent on
the temperature than the Maxwellian rates, as illustrated in
Figs. 8 and 9. This is a
direct consequence of the temperature dependance of the enhancement
factor: as this factor increases with decreasing temperature, the
Hybrid ionization rate decreases less steeply with temperature than
the Maxwellian rates. More precisely, as derived from the respective
expression of the rates at low temperature (respectively
Eqs. (A.2) and (A.10)),
the Maxwellian rate falls off exponentially (as
![]() )
with
decreasing temperature, whereas the Hybrid rate only decreases as a
power-law. As expected, one also notes that the modification of the
rates is more pronounced for lower value of
)
with
decreasing temperature, whereas the Hybrid rate only decreases as a
power-law. As expected, one also notes that the modification of the
rates is more pronounced for lower value of ![]() (compare the two
figures corresponding to
(compare the two
figures corresponding to
![]() and
and
![]() ).
).
![\begin{figure}
\par\includegraphics[width=6.8cm,clip]{MS1246f6.eps}\end{figure}](/articles/aa/full/2001/27/aa1246/Timg89.gif) |
Figure 6: Same as Fig. 5 for the different ions of iron. |
The radiative recombination rates are expected to be less affected by the Hybrid distribution, since the cross sections for recombination decrease with energy and no threshold exists. As the net effect of the high energy tail present in the hybrid distribution is to increase the median energy of the distribution (cf. Fig. 2), as compared to a Maxwellian, the radiative recombination rates are decreased.
To estimate the corresponding dumping factor,
![]() ,
we
follow the method used by Owocki & Scudder (1983). We
assume that the radiative recombination cross section varies as a
power-law in energy:
,
we
follow the method used by Owocki & Scudder (1983). We
assume that the radiative recombination cross section varies as a
power-law in energy:
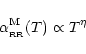 |
(10) |
The dumping factor computed for such a power-law cross section
(Eqs. (8) with (9)) is:
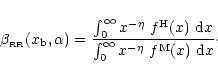 |
(11) |
![\begin{figure}
\par\includegraphics[width=7cm,clip]{MS1246f9.eps}\end{figure}](/articles/aa/full/2001/27/aa1246/Timg103.gif) |
Figure 9:
Same as Fig. 8 for |
However as we will see the correction factor is small, and we can
reasonably assume that it allows a fair estimate of the true Hybrid
radiative recombination rates. To minimize the errors, the Hybrid
radiative recombination rate has to be calculated from the best
estimate of the Maxwellian rates, multiplied by this approximation of
the dumping factor:
The parameters ![]() for the various ions are taken from Aldrovandi
& Péquignot (1973), when available. For other
ions we used a mean value of
for the various ions are taken from Aldrovandi
& Péquignot (1973), when available. For other
ions we used a mean value of ![]() corresponding to the mean
value
corresponding to the mean
value ![]() reported in Arnaud & Rothenflug (1985).
The exact value has a negligible effect on the estimation of the
radiative recombination rates.
reported in Arnaud & Rothenflug (1985).
The exact value has a negligible effect on the estimation of the
radiative recombination rates.
The dumping factor is plotted in Fig. 10 for the various ions
of oxygen. In that case a common ![]() value is used. The dumping
factor decreases with decreasing values of
value is used. The dumping
factor decreases with decreasing values of ![]() and
and ![]() ,
following the
increase of the distribution median energy. The modification is however
always modest, at most
,
following the
increase of the distribution median energy. The modification is however
always modest, at most ![]() for
for ![]() .
For iron, plotted in
Fig. 11 for
.
For iron, plotted in
Fig. 11 for ![]() ,
the value of
,
the value of ![]() slightly changes with
the considered ions, but this only yields negligible variations in the
dumping factor.
slightly changes with
the considered ions, but this only yields negligible variations in the
dumping factor.
The dielectronic recombination is a resonant process involving bound
states at discrete energies Ei and the rates have to be computed
by summing the contribution of many such bound states. According to
Arnaud & Raymond (1992), and Mazzotta et al.
(1998), the dielectronic recombination rates for a
Maxwellian distribution can be fitted accurately by the formula:
![\begin{figure}
\par\includegraphics[width=7.3cm,clip]{MS1246f11.eps}\end{figure}](/articles/aa/full/2001/27/aa1246/Timg112.gif) |
Figure 11:
Same as Fig. 10 for iron ions and |
Following again the method used by Owocki & Scudder
(1983), we thus assume that the corresponding dielectronic
recombination cross section can be approximated by:
To understand the effect of the hybrid distribution, let us assume
that only a single energy
![]() is dominant, corresponding to a simple
Dirac cross section at this energy. In that case, from
Eq. (8), the ratio of the dielectronic recombination
rate in a Hybrid distribution over that in a Maxwellian with the same
temperature,
is dominant, corresponding to a simple
Dirac cross section at this energy. In that case, from
Eq. (8), the ratio of the dielectronic recombination
rate in a Hybrid distribution over that in a Maxwellian with the same
temperature,
![]() ,
is simply the ratio of the Hybrid
to the Maxwellian function at the resonance energy. Its expression depends
on the position of the resonance energy with respect to the energy break.
In reduced energy coordinates, we obtain from Eqs. (4)
and (7):
,
is simply the ratio of the Hybrid
to the Maxwellian function at the resonance energy. Its expression depends
on the position of the resonance energy with respect to the energy break.
In reduced energy coordinates, we obtain from Eqs. (4)
and (7):
| = | |||
| = | 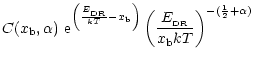 |
||
| (17) |
For
![]() (i.e. at high temperature or high value of
(i.e. at high temperature or high value of ![]() ),
the resonance lies in the Maxwellian part of the distribution.
),
the resonance lies in the Maxwellian part of the distribution.
![]() is independent of the temperature and the dielectronic recombination
rates are decreased, following the variation of the normalisation
factor,
is independent of the temperature and the dielectronic recombination
rates are decreased, following the variation of the normalisation
factor,
![]() ,
i.e. the decrease is modest (see Fig. 2).
,
i.e. the decrease is modest (see Fig. 2).
For
![]() the resonance lies in the power-law part of
the distribution. The increase of the dielectronic recombination rate
can be dramatic, increasing with decreasing
the resonance lies in the power-law part of
the distribution. The increase of the dielectronic recombination rate
can be dramatic, increasing with decreasing ![]() and
and ![]() .
.
These effects of the Hybrid distribution on the dielectronic
recombination rates are illustrated in Figs. 12 to 15, where we plotted the factor
![]() for various
ions and values of the parameters. The factors are computed exactly
from Eqs. (14) and (16).
for various
ions and values of the parameters. The factors are computed exactly
from Eqs. (14) and (16).
In Fig. 12 we consider O+6 at the temperature of
its maximum ionization fraction,
![]() .
For this ion
only one term is included in the rate estimate, with
.
For this ion
only one term is included in the rate estimate, with
![]() ,
and
,
and
![]() at the temperature considered. We plotted
the variation of
at the temperature considered. We plotted
the variation of
![]() with
with ![]() for
for ![]() ,
,
![]() and
and
![]() .
For
.
For
![]() the "resonance'' energy
the "resonance'' energy
![]() lies in the Maxwellian
part of the distribution and the dielectronic recombination rate is
decreased as compared to a Maxwellian, but by less than
lies in the Maxwellian
part of the distribution and the dielectronic recombination rate is
decreased as compared to a Maxwellian, but by less than ![]() ,
following the variation of the normalisation factor
,
following the variation of the normalisation factor
![]() .
For smaller values of
.
For smaller values of ![]() ,
the rate is increased significantly, up to a factor of 5 for
,
the rate is increased significantly, up to a factor of 5 for
![]() .
.
We consider other temperatures, fixing ![]() to
to ![]() ,
in
Fig. 13. Since we only consider the parameter range
,
in
Fig. 13. Since we only consider the parameter range
![]() ,
there is a threshold temperature,
,
there is a threshold temperature,
![]() ,
above which the resonance always falls in the
Maxwellian part. The dielectronic recombination rate is decreased via
the factor
,
above which the resonance always falls in the
Maxwellian part. The dielectronic recombination rate is decreased via
the factor
![]() .
This factor slightly decreases with
decreasing
.
This factor slightly decreases with
decreasing ![]() (cf. Fig. 2). At lower temperature, the resonance energy can fall
above the break, provided that
(cf. Fig. 2). At lower temperature, the resonance energy can fall
above the break, provided that ![]() is small enough (
is small enough (
![]() ).
This occurs at smaller
).
This occurs at smaller ![]() for higher temperature and the enhancement
at a given
for higher temperature and the enhancement
at a given ![]() increases with decreasing temperature.
increases with decreasing temperature.
![\begin{figure}
\par\includegraphics[width=7.3cm,clip]{MS1246f13.eps}\end{figure}](/articles/aa/full/2001/27/aa1246/Timg134.gif) |
Figure 13:
Same as Fig. 12 but the parameter |
![\begin{figure}
\par\includegraphics[width=7.3cm,clip]{MS1246f14.eps}\end{figure}](/articles/aa/full/2001/27/aa1246/Timg135.gif) |
Figure 14:
Same as Fig. 12 for the different ions of oxygen.
Each curve is labeled by the charge of the ion considered. The slope parameter is
fixed to |
![\begin{figure}
\par\includegraphics[width=7.3cm,clip]{MS1246f15.eps}\end{figure}](/articles/aa/full/2001/27/aa1246/Timg136.gif) |
Figure 15: Same as Fig. 14 for iron. |
We display in Figs. 14 and 15 the
variation of the factor
![]() with
with ![]() (for
(for ![]() ), for the
different ions of oxygen and iron, at the temperature of maximum
ionization fraction for a Maxwellian distribution under ionization
equilibrium. For most of the ions this temperature is above the
threshold temperature,
), for the
different ions of oxygen and iron, at the temperature of maximum
ionization fraction for a Maxwellian distribution under ionization
equilibrium. For most of the ions this temperature is above the
threshold temperature,
![]() ,
for all the resonances and
the dielectronic rate is
decreased. For the ions for which this is not the case (O+1,
O+6 and from Fe+1 to Fe+5), the dielectronic rate can be
increased significantly (by a factor between 2 to 5) provided
,
for all the resonances and
the dielectronic rate is
decreased. For the ions for which this is not the case (O+1,
O+6 and from Fe+1 to Fe+5), the dielectronic rate can be
increased significantly (by a factor between 2 to 5) provided ![]() is
small enough (typically
is
small enough (typically
![]() ). The increase starts as soon as
). The increase starts as soon as
![]() for the oxygen ions. The behavior of
for the oxygen ions. The behavior of
![]() is more
complex for the iron ions (two breaks in the variation of
is more
complex for the iron ions (two breaks in the variation of
![]() ), due
to the presence of more than one dominant resonance energy (more than one
term), taken into account in the computation of the dielectronic
rate.
), due
to the presence of more than one dominant resonance energy (more than one
term), taken into account in the computation of the dielectronic
rate.
In conclusion, the effect of the hybrid distribution on the
dielectronic rate depends on the position of the resonance energy as
compared to the power-law energy break. It can only be
increased if
![]() .
At high temperature, the
dielectronic recombination rate is slightly decreased.
.
At high temperature, the
dielectronic recombination rate is slightly decreased.
At
![]() ,
the
total rates are basically unchanged by the Hybrid distribution. For
,
the
total rates are basically unchanged by the Hybrid distribution. For
![]() (Fig. 16), the total rates are more
significantly changed. The radiative recombination rate increases
with decreasing temperature and it usually dominates the total
recombination rate in the low temperature range. As the dielectronic
rate is increased by the Hybrid distribution only at low temperature,
there are very few ions for which the total recombination rate can be
actually increased. This only occurs in a small temperature range, in
the rising part of the dielectronic rate. One also notes the expected
slight decrease of the radiative recombination rates (when it is
dominant at low temperature) and of the dielectronic rate at high
temperature.
(Fig. 16), the total rates are more
significantly changed. The radiative recombination rate increases
with decreasing temperature and it usually dominates the total
recombination rate in the low temperature range. As the dielectronic
rate is increased by the Hybrid distribution only at low temperature,
there are very few ions for which the total recombination rate can be
actually increased. This only occurs in a small temperature range, in
the rising part of the dielectronic rate. One also notes the expected
slight decrease of the radiative recombination rates (when it is
dominant at low temperature) and of the dielectronic rate at high
temperature.
Copyright ESO 2001