The Maxwellian distribution, generally considered for the electron
distribution in astrophysical plasmas,
![]() ,
is defined as:
,
is defined as:
It is convenient to express this distribution in term of the reduced energy
x=E/kT:
Non-Maxwellian electron distributions expected in the vicinity of
shock waves, as in young supernova remnants, seem to be reasonably
described by a Maxwellian distribution at low energy up to a break
energy ![]() ,
and by a power-law distribution at higher energy
(e.g., Berezhko & Ellison 1999; Bykov & Uvarov
1999). We call hereafter this "Maxwellian/Power-law''
type of electron distribution the Hybrid electron distribution
(
,
and by a power-law distribution at higher energy
(e.g., Berezhko & Ellison 1999; Bykov & Uvarov
1999). We call hereafter this "Maxwellian/Power-law''
type of electron distribution the Hybrid electron distribution
(![]() ). It is defined, in reduced energy coordinates, as:
). It is defined, in reduced energy coordinates, as:
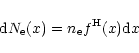 |
(5) |
The normalisation factor of the power-law distribution is defined so that the electron distribution is continous at ![]() .
The factor
.
The factor
![]() is a normalisation constant, so that
is a normalisation constant, so that
![]() :
:
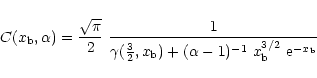 |
(7) |
The Hybrid distributions
![]() ,
obtained for several values
of the energy break
,
obtained for several values
of the energy break ![]() ,
are compared to the Maxwellian
distribution in Fig. 1. The slope has been fixed to
,
are compared to the Maxwellian
distribution in Fig. 1. The slope has been fixed to
![]() ,
a typical value found in the models referenced above. The
variation of the reduced median energy of the distribution with
,
a typical value found in the models referenced above. The
variation of the reduced median energy of the distribution with
![]() ,
for
,
for
![]() ,
is plotted in Fig. 2, as
well as the variation of the normalisation factor
,
is plotted in Fig. 2, as
well as the variation of the normalisation factor
![]() .
.
As apparent in the figures, there is a critical value of ![]() ,
for
each
,
for
each ![]() value, corresponding to a qualitative change in the
behavior of the Hybrid distribution. This can be understood by
looking at the distribution at the break energy
value, corresponding to a qualitative change in the
behavior of the Hybrid distribution. This can be understood by
looking at the distribution at the break energy ![]() .
Whereas the
distribution is continuous, its slope changes. The logarithmic slope
is
.
Whereas the
distribution is continuous, its slope changes. The logarithmic slope
is
![]() on the Maxwellian side and
on the Maxwellian side and ![]() on the power-law side.
There is no break in the shape of the Hybrid distribution (full line
in Fig. 1), only for the critical value of
on the power-law side.
There is no break in the shape of the Hybrid distribution (full line
in Fig. 1), only for the critical value of
![]() .
For
.
For
![]() ,
the power-law always decreases less rapidly with
energy than a Maxwellian distribution and does correspond to an enhanced high energy tail. The contribution of this tail increases
with decreasing
,
the power-law always decreases less rapidly with
energy than a Maxwellian distribution and does correspond to an enhanced high energy tail. The contribution of this tail increases
with decreasing ![]() (and
(and ![]() ). Thus the median energy increases
and the normalisation parameter, which scales the Maxwellian part,
decreases (see Fig. 2). On the other hand, when
). Thus the median energy increases
and the normalisation parameter, which scales the Maxwellian part,
decreases (see Fig. 2). On the other hand, when
![]() ,
there is an intermediate region above the
energy break where the power-law decreases more steeply than a
Maxwellian (see dotted line in Fig. 1). This results in
a deficit of electrons at these energies as compared to a Maxwellian
distribution, more and more pronounced as
,
there is an intermediate region above the
energy break where the power-law decreases more steeply than a
Maxwellian (see dotted line in Fig. 1). This results in
a deficit of electrons at these energies as compared to a Maxwellian
distribution, more and more pronounced as ![]() is small. The median
energy thus starts to decrease with decreasing
is small. The median
energy thus starts to decrease with decreasing ![]() and can be even
lower than the median energy of a Maxwellian distribution
(Fig. 2). In this paper we only consider the
regime where
and can be even
lower than the median energy of a Maxwellian distribution
(Fig. 2). In this paper we only consider the
regime where
![]() .
It corresponds to clear cases where the
high energy part of the distribution is indeed increased, as expected
when electron are accelerated in shocks. Furthermore, the
distribution used here is only an approximation, valid when the hard
tail can be considered as a perturbation of the original Maxwellian
distribution. The simulations of Bykov & Uvarov (1999,
see their Fig. 2) clearly show that the low energy part of the
distribution is less and less well approximated by a Maxwellian
distribution, as the "enhanced'' high energy tail extends to lower and
lower energy (lower "break''). Although we cannot rigorously define
a corresponding quantitative lower limit on
.
It corresponds to clear cases where the
high energy part of the distribution is indeed increased, as expected
when electron are accelerated in shocks. Furthermore, the
distribution used here is only an approximation, valid when the hard
tail can be considered as a perturbation of the original Maxwellian
distribution. The simulations of Bykov & Uvarov (1999,
see their Fig. 2) clearly show that the low energy part of the
distribution is less and less well approximated by a Maxwellian
distribution, as the "enhanced'' high energy tail extends to lower and
lower energy (lower "break''). Although we cannot rigorously define
a corresponding quantitative lower limit on ![]() ,
the cases presented
by Bykov & Uvarov (1999, see their Fig. 2) suggest a
limit similar to the one considered here, i.e. a few times the
Maxwellian peak energy.
,
the cases presented
by Bykov & Uvarov (1999, see their Fig. 2) suggest a
limit similar to the one considered here, i.e. a few times the
Maxwellian peak energy.
The distribution considered here differs from the so-called
"kappa-distribution'' or the "power distribution'', relevant for
other physical conditions (see e.g. Dzifcáková 2000 and references therein). These two distributions have been used to
model deviations from a Maxwellian distribution caused by strong
plasma inhomogeneities, as in the solar corona, and their impact on
the ionization balance has been extensively studied (e.g. Roussel-Dupré 1980; Owocki & Scudder 1983; Dzifcáková 1992; Dzifcáková 1998). Although the effect of the Hybrid distribution
is expected to be qualitatively similar, it has never been
quantitatively studied. In the next section we discuss how the
ionization and recombination rates are modified, as compared to a pure
Maxwellian distribution, depending on the parameters ![]() and
and ![]() .
.
Copyright ESO 2001