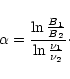 |
Figure 4:
Run of the red-band brightness and optical spectral index
along the outer half of the jet in 3C273, for a 0
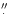 2
beam. 2
beam.
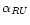 was determined from Figs. 1 and 2, while
was determined from Figs. 1 and 2, while
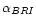 for a 1
for a 1
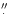 3 beam is taken from
Röser & Meisenheimer (1991). For comparison, we show 3 beam is taken from
Röser & Meisenheimer (1991). For comparison, we show
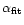 ,
the corresponding spectral
index obtained from synchrotron
spectra fitted by Meisenheimer et al. (1996a) and Röser et al. (2000). While the
observed spectral index agrees with older data, it is now clear that
the fit is inadequate for the optical part of the spectrum. The
steeper spectral index of the fit may either be
due to contamination of the infrared flux by a "backflow'' component
around the jet, or because of the presence of a second high-energy electron
population in the jet which is not included in the fit (see
Sect. 6.3.1 for a discussion of the discrepancies). ,
the corresponding spectral
index obtained from synchrotron
spectra fitted by Meisenheimer et al. (1996a) and Röser et al. (2000). While the
observed spectral index agrees with older data, it is now clear that
the fit is inadequate for the optical part of the spectrum. The
steeper spectral index of the fit may either be
due to contamination of the infrared flux by a "backflow'' component
around the jet, or because of the presence of a second high-energy electron
population in the jet which is not included in the fit (see
Sect. 6.3.1 for a discussion of the discrepancies). |