

Up: HST optical spectral index 3C273
Subsections
6 Discussion
6.1 The jet's extensions
Before analysing the jet emission proper, we consider the relation of
the extensions to the jet. Our new images confirm the outer
extension's nature as spiral galaxy. The spectral index map gives us
few hints about the nature of the emission mechanism for the
inner and southern extensions. We have therefore measured
their integral fluxes at 300nm and 620nm (this paper) and
at 1.6 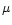 (HST NICMOS camera 2 imaging
(HST NICMOS camera 2 imaging![[*]](/icons/foot_motif.gif) ,
in prep.). Figure 5 shows the resulting
spectral energy distributions. In1, with the steepest
,
in prep.). Figure 5 shows the resulting
spectral energy distributions. In1, with the steepest
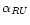 ,
is also the brightest in the infrared. The infrared flux points of
both extension S and of In2 lie on the continuation of the power law
with index -0.4, determined on the optical spectral index map. If
this power law were valid up to radio wavelengths, it would predict a
flux at
,
is also the brightest in the infrared. The infrared flux points of
both extension S and of In2 lie on the continuation of the power law
with index -0.4, determined on the optical spectral index map. If
this power law were valid up to radio wavelengths, it would predict a
flux at 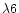 cm of about 50
cm of about 50 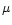 Jy for the northwestern knot
In1, and of about 45
Jy for the northwestern knot
In1, and of about 45 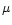 Jy for the southern extension S. This is a
factor of order 100 below the flux from the jet at this wavelength
(Conway et al. 1993), and any emission at this level would not be detected
even on our new VLA maps with an rms noise of
Jy for the southern extension S. This is a
factor of order 100 below the flux from the jet at this wavelength
(Conway et al. 1993), and any emission at this level would not be detected
even on our new VLA maps with an rms noise of 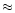 0.8mJy.
There is no similarly obvious extrapolation of In1's SED to radio
wavelengths. A full comparison will be presented in a future paper.
The inner extension shows a polarisation signal on unpublished
ground-based maps made by our group and on polarimetric images
obtained with the Faint Object Camera on board HST (Thomson et al. 1993). A
polarisation signal could be due to scattered quasar light
(Röser & Meisenheimer 1991) or, together with possible radio emission, synchrotron
radiation. We aim to clarify the nature of the inner extensions by
planned polarimetric and spectroscopic observations with the VLT.
0.8mJy.
There is no similarly obvious extrapolation of In1's SED to radio
wavelengths. A full comparison will be presented in a future paper.
The inner extension shows a polarisation signal on unpublished
ground-based maps made by our group and on polarimetric images
obtained with the Faint Object Camera on board HST (Thomson et al. 1993). A
polarisation signal could be due to scattered quasar light
(Röser & Meisenheimer 1991) or, together with possible radio emission, synchrotron
radiation. We aim to clarify the nature of the inner extensions by
planned polarimetric and spectroscopic observations with the VLT.
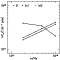 |
Figure 5:
Broad-band flux points for the radio-quiet extensions to
the jet from HST imaging at 1.6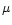 ,
620nm and 300nm. ,
620nm and 300nm. |
6.2 The hot spot
The optical counterpart to the radio hot
spot (H2) appears very faint on both images, and the spectral
index map shows a flip from flat to steep there. Both features
are explained by the Meisenheimer & Heavens (1986) hot spot model: the lifetime of
electrons emitting in the optical is quenched by the strong
magnetic field in the hot spot. The spectral index flip is
expected if there is an offset between the emission peaks at
different frequencies. This offset is predicted by the theory by
Meisenheimer & Heavens (1986) and is clearly seen when comparing optical and radio
images (Röser et al. 1997; a detailed comparison of all data will
be presented in a future paper). By its spectrum and morphology,
the hot spot appears exactly as expected for a high-loss
synchrotron emission region downstream of a localized strong shock
with first-order Fermi acceleration. Finally, we note that
although the term "hot spot'' is historically in use for this
part of the jet, the term is ill-defined and may have become
inadequate, but we defer a discussion of its adequacy to a future
paper.
6.3 Main body of the jet
Our HST images (Figs. 1 and 2) show a close
coincidence of the jet's morphology over a factor of 2 in frequency
(optical and UV). The spectral index map (Fig. 3) shows
amazingly smooth variations in the physical conditions over the entire
jet. The electrons' synchrotron cooling leaves little imprint on the
spectral index along the jet, contrary to expectations.
6.3.1 The spectral index at HST resolution
 |
Figure 6:
Optical spectral index against red-band brightness for the
outer half of the jet in 3C273 (data as in Fig. 4).
There is no strict correlation like that observed in the jet of M 87. |
The two striking features of our spectral index map are the smooth
variation of the spectral index over the entire jet
(Fig. 4), and the lack of a strong correlation
between red-band brightness and spectral index
(Fig. 6) like that observed in the jet of M 87
(Meisenheimer et al. 1996a,b; Perlman et al. 2001). There are large but smooth variations
of the spectral index, while the surface brightness remains fairly
constant over the jet's projected extent of about 10
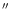 .
Conversely, there are large local variations of surface
brightness without strong changes in the spectral index. We do
not observe abrupt changes of the spectral index inside the jet
like we do in the hot spot. The run of the spectral index is thus
consistent with the complete absence of energy losses over scales
of many kiloparsecs, in spite of the large observed synchrotron
luminosity, which indicates the need for re-acceleration of
particles inside the jet. The mismatch between synchrotron
cooling scale and extent of the jet even led Guthrie & Napier (1975) to
conclude that the jet's emission could not be synchrotron
radiation.
The same lack of apparent synchrotron cooling is implied by the
surprising overall correspondence between
.
Conversely, there are large local variations of surface
brightness without strong changes in the spectral index. We do
not observe abrupt changes of the spectral index inside the jet
like we do in the hot spot. The run of the spectral index is thus
consistent with the complete absence of energy losses over scales
of many kiloparsecs, in spite of the large observed synchrotron
luminosity, which indicates the need for re-acceleration of
particles inside the jet. The mismatch between synchrotron
cooling scale and extent of the jet even led Guthrie & Napier (1975) to
conclude that the jet's emission could not be synchrotron
radiation.
The same lack of apparent synchrotron cooling is implied by the
surprising overall correspondence between
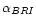 and
and
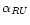 (Fig. 4) which have been determined at
vastly different resolutions (1
(Fig. 4) which have been determined at
vastly different resolutions (1
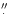 3 and 0
3 and 0
 2, corresponding to
4.2h60kpc and 640h60pc, respectively). The small
differences (strongest in regions A and C2/D1) can be explained at
least in part by the different beam sizes: the spectral index
determined by smoothing the HST images to 1
2, corresponding to
4.2h60kpc and 640h60pc, respectively). The small
differences (strongest in regions A and C2/D1) can be explained at
least in part by the different beam sizes: the spectral index
determined by smoothing the HST images to 1
 3 makes the
discrepancy smaller. In addition, the emission region becomes wider
towards longer wavelengths, an effect already noticeable in the
near-infrared
3 makes the
discrepancy smaller. In addition, the emission region becomes wider
towards longer wavelengths, an effect already noticeable in the
near-infrared 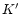 band (Neumann et al. 1997) and attributed to a
"backflow'' (Röser et al. 1996). The presence of such a steep-spectrum,
diffuse component more extended than the jet channel might also
explain the discrepancy.
The general agreement indicates a constancy of the shape of the
spectrum even at the scales resolved by HST. To first order, the
appearance of the jet at all wavelengths can be explained through such
a constant spectral shape consisting of a low-frequency power law and
a high-frequency curved cutoff. The assumed spectral shape is shifted
systematically in the
band (Neumann et al. 1997) and attributed to a
"backflow'' (Röser et al. 1996). The presence of such a steep-spectrum,
diffuse component more extended than the jet channel might also
explain the discrepancy.
The general agreement indicates a constancy of the shape of the
spectrum even at the scales resolved by HST. To first order, the
appearance of the jet at all wavelengths can be explained through such
a constant spectral shape consisting of a low-frequency power law and
a high-frequency curved cutoff. The assumed spectral shape is shifted
systematically in the
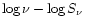 plane, passing different
parts of the curved cutoff through the optical flux point. This leads
to similar morphological features at all wavelengths, in accord with
observations (Conway et al. 1993; Bahcall et al. 1995). Moving the spectral shape
through a constant optical flux point leads to a correlation of
steeper optical spectral index with higher radio flux. This
correlation reproduces the observed tenfold increase of the radio
surface brightness from A to D2/H3 (Conway et al. 1993) and the overall
steepening of the optical spectral index. However, this steepening
happens on much longer time scales than expected from synchrotron
cooling alone.
Assuming an electron energy distribution with a fairly sharp cutoff,
drastic jumps in
plane, passing different
parts of the curved cutoff through the optical flux point. This leads
to similar morphological features at all wavelengths, in accord with
observations (Conway et al. 1993; Bahcall et al. 1995). Moving the spectral shape
through a constant optical flux point leads to a correlation of
steeper optical spectral index with higher radio flux. This
correlation reproduces the observed tenfold increase of the radio
surface brightness from A to D2/H3 (Conway et al. 1993) and the overall
steepening of the optical spectral index. However, this steepening
happens on much longer time scales than expected from synchrotron
cooling alone.
Assuming an electron energy distribution with a fairly sharp cutoff,
drastic jumps in
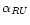 would be expected at the locations of
the shock fronts if the jet knots were (strong) shocks like the hot
spot without extended re-acceleration acting between them. The
absence of strong cooling makes it impossible to pinpoint localised
sites at which particles are either exclusively accelerated or
exclusively undergo strong losses. Any acceleration site must
therefore be considerably smaller than the beam size we used
(
640h60-1pc), and these acceleration sites must be
distributed over the entire jet to explain the absence of
cooling. This, together with the low-frequency spectral index of
would be expected at the locations of
the shock fronts if the jet knots were (strong) shocks like the hot
spot without extended re-acceleration acting between them. The
absence of strong cooling makes it impossible to pinpoint localised
sites at which particles are either exclusively accelerated or
exclusively undergo strong losses. Any acceleration site must
therefore be considerably smaller than the beam size we used
(
640h60-1pc), and these acceleration sites must be
distributed over the entire jet to explain the absence of
cooling. This, together with the low-frequency spectral index of
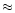 -0.8, corresponds to the jet-like acceleration mechanism
proposed by Meisenheimer et al. (1997).
Meisenheimer et al. (1996a) have presented fits of synchrotron continua to the
observed SEDs of knots A, B, C, D and the hot spot H at 1
-0.8, corresponds to the jet-like acceleration mechanism
proposed by Meisenheimer et al. (1997).
Meisenheimer et al. (1996a) have presented fits of synchrotron continua to the
observed SEDs of knots A, B, C, D and the hot spot H at 1
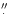 3
which have also been used by Röser et al. (2000). It is noted that the
optical spectral index predicted from these spectra
(
3
which have also been used by Röser et al. (2000). It is noted that the
optical spectral index predicted from these spectra
(
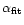 in Fig. 4) is always
steeper than the observed spectral index, that is below
in Fig. 4) is always
steeper than the observed spectral index, that is below
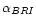 and
and
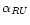 .
This indicates that the fitted
spectrum is not fully adequate at the highest frequencies. This
may again be due to contamination of the near-infrared flux by the
same "backflow'' component mentioned above. The contamination
would make the IR-optical spectral index (which dominates the run
of the spectrum at high frequencies) steeper than the optical
spectral index, as observed. Alternatively or additionally, there
could be deviations of the optical-UV spectral shape from a
standard synchrotron cutoff spectrum which may be interpreted as
the first observational hint towards the existence of a second,
higher-energy electron population producing the X-ray emission
(Röser et al. 2000). Detailed statements about the adequacy of model
spectra have to be deferred to a future paper considering the full
radio, infrared and optical data set.
.
This indicates that the fitted
spectrum is not fully adequate at the highest frequencies. This
may again be due to contamination of the near-infrared flux by the
same "backflow'' component mentioned above. The contamination
would make the IR-optical spectral index (which dominates the run
of the spectrum at high frequencies) steeper than the optical
spectral index, as observed. Alternatively or additionally, there
could be deviations of the optical-UV spectral shape from a
standard synchrotron cutoff spectrum which may be interpreted as
the first observational hint towards the existence of a second,
higher-energy electron population producing the X-ray emission
(Röser et al. 2000). Detailed statements about the adequacy of model
spectra have to be deferred to a future paper considering the full
radio, infrared and optical data set.
6.3.2 Can beaming account for the lack of cooling?
Heinz & Begelman (1997) proposed that sub-equipartition magnetic fields
combined with mildly relativistic beaming could explain the lack
of cooling in the jet of M 87 - which is, however, ten times
shorter than that of 3C273. As an alternative to postulating
re-acceleration, we consider whether low magnetic field values and
beaming could lead to electron lifetimes sufficient to allow
electrons to be accelerated at region A to illuminate the entire
jet down to the hot spot over a projected extent of
32
h60-1kpc (the argument will become even more stringent by
demanding acceleration in the quasar core). We consider the
electron lifetime against synchrotron and inverse Compton cooling
off cosmic microwave background photons; the synchrotron
self-Compton process is negligible for electrons in the jet
(Röser et al. 2000), as is Compton scattering off the host galaxy's star
light.
The total energy loss rate of an electron with energy E due to
synchrotron radiation and inverse Compton scattering, averaged
over many pitch-angle scattering events during its lifetime, is
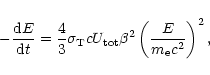 |
(4) |
where
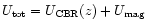 is the sum of the energy densities of the background
radiation and magnetic field, respectively, and
is the sum of the energy densities of the background
radiation and magnetic field, respectively, and
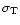 is the Thomson cross-section
(Longair 1994). We integrate this equation from
is the Thomson cross-section
(Longair 1994). We integrate this equation from 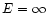 at t=0 to E(t), assuming
at t=0 to E(t), assuming 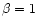 (appropriate for the
highly relativistic electrons required for optical synchrotron
radiation) and substitute for the electron's energy
(appropriate for the
highly relativistic electrons required for optical synchrotron
radiation) and substitute for the electron's energy
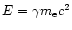 .
Inverting yields the maximum time that can have
elapsed since an electron was accelerated, given its Lorentz
factor
.
Inverting yields the maximum time that can have
elapsed since an electron was accelerated, given its Lorentz
factor 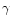 (van der Laan & Perola 1969):
(van der Laan & Perola 1969):
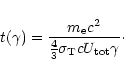 |
(5) |
This is the "electron lifetime'', inversely
proportional to both the energy density in which the electron has
been "ageing'', and the electron's own energy.
As most of the electron's energy is radiated at the synchrotron
characteristic frequency
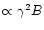 ,
we can substitute
for
,
we can substitute
for 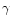 in Eq. (5) in terms of the observing
frequency and the magnetic field in the source. Hence,
Eq. (5) becomes (in convenient units)
in Eq. (5) in terms of the observing
frequency and the magnetic field in the source. Hence,
Eq. (5) becomes (in convenient units)
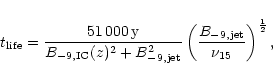 |
(6) |
where
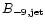 is the magnetic flux density in nT of the
jet field, the background radiation energy density has been
expressed in terms of an equivalent magnetic field,
is the magnetic flux density in nT of the
jet field, the background radiation energy density has been
expressed in terms of an equivalent magnetic field,
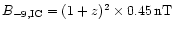 ,
and
,
and
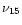 is the observing frequency in 1015Hz
(van der Laan & Perola 1969). Note that as the substituted
is the observing frequency in 1015Hz
(van der Laan & Perola 1969). Note that as the substituted
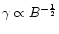 ,
setting
,
setting
 is now meaningless.
To be fully adequate for electrons in a relativistic jet at
cosmological distances, the equation needs to be modified. Firstly,
the frequency local to the source is (1+z) times the observing
frequency because of the cosmological redshift. Furthermore, the
radiating electron may be embedded in a relativistic flow with bulk
Lorentz factor
is now meaningless.
To be fully adequate for electrons in a relativistic jet at
cosmological distances, the equation needs to be modified. Firstly,
the frequency local to the source is (1+z) times the observing
frequency because of the cosmological redshift. Furthermore, the
radiating electron may be embedded in a relativistic flow with bulk
Lorentz factor 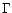 with three consequences: relativistic time
dilation and Doppler shift, and boost of the background radiation
energy density. The relativistic time dilation enhances the electron
lifetime in the jet frame by a factor
with three consequences: relativistic time
dilation and Doppler shift, and boost of the background radiation
energy density. The relativistic time dilation enhances the electron
lifetime in the jet frame by a factor 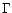 .
The Doppler shift
between the emission frequency
.
The Doppler shift
between the emission frequency
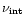 in the jet frame
(equal to the characteristic frequency) and the observation frequency
in the jet frame
(equal to the characteristic frequency) and the observation frequency
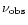 is given by
is given by
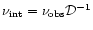 ,
where
,
where
![${\cal
D}(\Gamma,\theta) = [\Gamma(1-\beta_{{\rm jet}} \cos
\theta)]^{-1}$](/articles/aa/full/2001/26/aa1311/img81.gif) ,
the Doppler boosting factor for an angle
,
the Doppler boosting factor for an angle 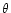 to
the line of sight (see Hughes & Miller 1991, e.g.). A relativistic
flow perceives the energy density of the background radiation field
boosted up by a factor
to
the line of sight (see Hughes & Miller 1991, e.g.). A relativistic
flow perceives the energy density of the background radiation field
boosted up by a factor 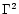 (Dermer 1995). Inserting these
yields
(Dermer 1995). Inserting these
yields
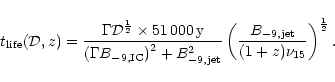 |
(7) |
The electron lifetime attains a maximum value at a certain value of
the jet's magnetic field (Fig. 7) (van der Laan & Perola 1969). On
either side of the maximum, the lifetime is decreased by larger losses
suffered before it is observed: for a higher magnetic field in
the jet, the synchrotron cooling is more rapid (
 ,
Eq. (5)).
,
Eq. (5)).
 |
Figure 7:
Maximum
age against synchrotron and inverse Compton cooling (off microwave
background photons at 3C273's redshift) of an electron radiating at observed UV
wavelengths plotted against the jet magnetic field.
Solid line, no beaming; dashed line, relativistic
Doppler boosting with 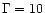 and a line-of-sight
angle
and a line-of-sight
angle
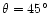 . . |
A lower jet field requires an
electron of higher Lorentz factor for emission at the given frequency,
which also suffers more rapid losses (
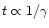 ,
Eq. (5)). By differentiation of Eq. (7), the
value of the maximum lifetime is
,
Eq. (5)). By differentiation of Eq. (7), the
value of the maximum lifetime is
![\begin{displaymath}%
t_{{\rm max}}(B_{{\rm IC}}, {\cal D}, z) = \sqrt{\frac{\cal...
...\frac{3}{2}} \left[(1+z)
\nu_{15}\right]^{\frac{1}{2}} }\cdot
\end{displaymath}](/articles/aa/full/2001/26/aa1311/img88.gif) |
(8) |
Note that
the largest possible value for the factor
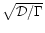 is
is
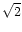 .
.
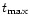 is a firm upper limit for the lifetime
of a synchrotron-radiating electron from a source at redshift z in a
flow of bulk Lorentz factor
is a firm upper limit for the lifetime
of a synchrotron-radiating electron from a source at redshift z in a
flow of bulk Lorentz factor 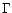 ,
whatever the magnetic field
strength in the source. It is deduced only from the fact that
synchrotron emission is observed at a certain frequency, and that
electrons which can radiate at this frequency suffer drastic energy
losses either by synchrotron or by inverse Compton cooling between the
time of acceleration and the time of emission. The only additional
assumptions are rapid pitch-angle scattering and a homogeneity of
conditions throughout the electron's lifetime.
,
whatever the magnetic field
strength in the source. It is deduced only from the fact that
synchrotron emission is observed at a certain frequency, and that
electrons which can radiate at this frequency suffer drastic energy
losses either by synchrotron or by inverse Compton cooling between the
time of acceleration and the time of emission. The only additional
assumptions are rapid pitch-angle scattering and a homogeneity of
conditions throughout the electron's lifetime.
The VLBI jet close to the core has a line-of-sight angle near
10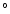 and a bulk Lorentz factor near 10 (Abraham & Romeo 1999). A
line-of-sight angle
and a bulk Lorentz factor near 10 (Abraham & Romeo 1999). A
line-of-sight angle
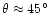 has been inferred for
the flow into the hot spot from independent considerations of the
jet's polarisation change there and the hot spot's morphology
(Conway & Davis 1994; Meisenheimer et al. 1997). We have plotted the lifetime of an electron
responsible for emission from the jet in 3C273 observed at
300nm as function of the jet's magnetic field in
Fig. 7 for the extreme cases of no beaming in the
optical jet and beaming identical to that in the VLBI jet with
has been inferred for
the flow into the hot spot from independent considerations of the
jet's polarisation change there and the hot spot's morphology
(Conway & Davis 1994; Meisenheimer et al. 1997). We have plotted the lifetime of an electron
responsible for emission from the jet in 3C273 observed at
300nm as function of the jet's magnetic field in
Fig. 7 for the extreme cases of no beaming in the
optical jet and beaming identical to that in the VLBI jet with
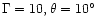 ,
and for an intermediate case with
,
and for an intermediate case with
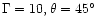 (though note that
(though note that
 is unrealistic as there is a difference in position angle
between the VLBI jet at 244
is unrealistic as there is a difference in position angle
between the VLBI jet at 244 and the arcsecond jet at
222
and the arcsecond jet at
222 ).
The equipartition flux densities derived for the jet lie in the
range of 15nT (Neumann 1995) up to 67nT for regionA
(Röser et al. 2000), leading to maximum ages of 100-800 years, less
than the light travel time from one bright region to the next. In
the absence of beaming effects, the largest possible lifetime for
electrons in 3C273 from Eq. (8) is about
58000y, again short of the required values. The "boosted
lifetime'' can be at most
).
The equipartition flux densities derived for the jet lie in the
range of 15nT (Neumann 1995) up to 67nT for regionA
(Röser et al. 2000), leading to maximum ages of 100-800 years, less
than the light travel time from one bright region to the next. In
the absence of beaming effects, the largest possible lifetime for
electrons in 3C273 from Eq. (8) is about
58000y, again short of the required values. The "boosted
lifetime'' can be at most 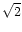 larger than this. There is
thus no combination of
larger than this. There is
thus no combination of
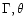 which enhances the
electron lifetime to the 100000y required for illumination of
the entire jet in 3C 273 by UV-radiating electrons.
Thus, the invocation of mild or even drastic beaming and/or
sub-equipartition fields cannot resolve the discrepancy between the
synchrotron loss scale and the extent of the optical jet of 3C273,
as has been possible for the jet in M 87 (Heinz & Begelman 1997). As another
alternative to invoking quasi-permanent re-acceleration, the existence
of a "loss-free channel'' in which electrons can travel down a jet
without synchrotron cooling has been proposed by Owen et al. (1989). As
an extreme version of this case, we assume that the electron travels
along the jet in zero magnetic field and is observed as soon as it
enters a filament with magnetic field
which enhances the
electron lifetime to the 100000y required for illumination of
the entire jet in 3C 273 by UV-radiating electrons.
Thus, the invocation of mild or even drastic beaming and/or
sub-equipartition fields cannot resolve the discrepancy between the
synchrotron loss scale and the extent of the optical jet of 3C273,
as has been possible for the jet in M 87 (Heinz & Begelman 1997). As another
alternative to invoking quasi-permanent re-acceleration, the existence
of a "loss-free channel'' in which electrons can travel down a jet
without synchrotron cooling has been proposed by Owen et al. (1989). As
an extreme version of this case, we assume that the electron travels
along the jet in zero magnetic field and is observed as soon as it
enters a filament with magnetic field
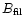 .
The energy
loss between acceleration and synchrotron emission is then only due to
inverse Compton scattering. The lifetime in 3C273 is then
130000y
.
The energy
loss between acceleration and synchrotron emission is then only due to
inverse Compton scattering. The lifetime in 3C273 is then
130000y
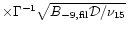 .
Again, if the jet flow in 3C273 is highly
relativistic, the electrons suffer heavy inverse Compton losses and
the lifetime mismatch persists. In any case, it remains to be shown
that the "loss-free channel'' is a physically feasible configuration
of an MHD jet.
.
Again, if the jet flow in 3C273 is highly
relativistic, the electrons suffer heavy inverse Compton losses and
the lifetime mismatch persists. In any case, it remains to be shown
that the "loss-free channel'' is a physically feasible configuration
of an MHD jet.


Up: HST optical spectral index 3C273
Copyright ESO 2001



![]() and a bulk Lorentz factor near 10 (Abraham & Romeo 1999). A
line-of-sight angle
and a bulk Lorentz factor near 10 (Abraham & Romeo 1999). A
line-of-sight angle
![]() has been inferred for
the flow into the hot spot from independent considerations of the
jet's polarisation change there and the hot spot's morphology
(Conway & Davis 1994; Meisenheimer et al. 1997). We have plotted the lifetime of an electron
responsible for emission from the jet in 3C273 observed at
300nm as function of the jet's magnetic field in
Fig. 7 for the extreme cases of no beaming in the
optical jet and beaming identical to that in the VLBI jet with
has been inferred for
the flow into the hot spot from independent considerations of the
jet's polarisation change there and the hot spot's morphology
(Conway & Davis 1994; Meisenheimer et al. 1997). We have plotted the lifetime of an electron
responsible for emission from the jet in 3C273 observed at
300nm as function of the jet's magnetic field in
Fig. 7 for the extreme cases of no beaming in the
optical jet and beaming identical to that in the VLBI jet with
![]() ,
and for an intermediate case with
,
and for an intermediate case with
![]() (though note that
(though note that
![]() is unrealistic as there is a difference in position angle
between the VLBI jet at 244
is unrealistic as there is a difference in position angle
between the VLBI jet at 244![]() and the arcsecond jet at
222
and the arcsecond jet at
222![]() ).
The equipartition flux densities derived for the jet lie in the
range of 15nT (Neumann 1995) up to 67nT for regionA
(Röser et al. 2000), leading to maximum ages of 100-800 years, less
than the light travel time from one bright region to the next. In
the absence of beaming effects, the largest possible lifetime for
electrons in 3C273 from Eq. (8) is about
58000y, again short of the required values. The "boosted
lifetime'' can be at most
).
The equipartition flux densities derived for the jet lie in the
range of 15nT (Neumann 1995) up to 67nT for regionA
(Röser et al. 2000), leading to maximum ages of 100-800 years, less
than the light travel time from one bright region to the next. In
the absence of beaming effects, the largest possible lifetime for
electrons in 3C273 from Eq. (8) is about
58000y, again short of the required values. The "boosted
lifetime'' can be at most ![]() larger than this. There is
thus no combination of
larger than this. There is
thus no combination of
![]() which enhances the
electron lifetime to the 100000y required for illumination of
the entire jet in 3C 273 by UV-radiating electrons.
Thus, the invocation of mild or even drastic beaming and/or
sub-equipartition fields cannot resolve the discrepancy between the
synchrotron loss scale and the extent of the optical jet of 3C273,
as has been possible for the jet in M 87 (Heinz & Begelman 1997). As another
alternative to invoking quasi-permanent re-acceleration, the existence
of a "loss-free channel'' in which electrons can travel down a jet
without synchrotron cooling has been proposed by Owen et al. (1989). As
an extreme version of this case, we assume that the electron travels
along the jet in zero magnetic field and is observed as soon as it
enters a filament with magnetic field
which enhances the
electron lifetime to the 100000y required for illumination of
the entire jet in 3C 273 by UV-radiating electrons.
Thus, the invocation of mild or even drastic beaming and/or
sub-equipartition fields cannot resolve the discrepancy between the
synchrotron loss scale and the extent of the optical jet of 3C273,
as has been possible for the jet in M 87 (Heinz & Begelman 1997). As another
alternative to invoking quasi-permanent re-acceleration, the existence
of a "loss-free channel'' in which electrons can travel down a jet
without synchrotron cooling has been proposed by Owen et al. (1989). As
an extreme version of this case, we assume that the electron travels
along the jet in zero magnetic field and is observed as soon as it
enters a filament with magnetic field
![]() .
The energy
loss between acceleration and synchrotron emission is then only due to
inverse Compton scattering. The lifetime in 3C273 is then
130000y
.
The energy
loss between acceleration and synchrotron emission is then only due to
inverse Compton scattering. The lifetime in 3C273 is then
130000y
![]() .
Again, if the jet flow in 3C273 is highly
relativistic, the electrons suffer heavy inverse Compton losses and
the lifetime mismatch persists. In any case, it remains to be shown
that the "loss-free channel'' is a physically feasible configuration
of an MHD jet.
.
Again, if the jet flow in 3C273 is highly
relativistic, the electrons suffer heavy inverse Compton losses and
the lifetime mismatch persists. In any case, it remains to be shown
that the "loss-free channel'' is a physically feasible configuration
of an MHD jet.