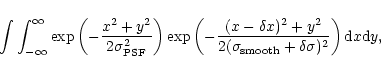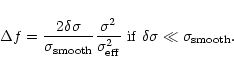Up: HST optical spectral index 3C273
Subsections
Appendix A: Image alignment
A.1 Flux errors from misalignment
Consider two images which are not registered correctly and which have
slightly different PSF widths. When performing photometry on these
images, we assume that they are registered perfectly and have
identical, known beam sizes. This amounts to making a flux
measurement in a certain aperture in one image, but in a slightly
offset aperture of slightly different size in the second image. The
error is largest in the steepest gradients in the image, which are the
flanks of the PSF of width 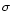 ,
smoothed to the desired effective
beam size
,
smoothed to the desired effective
beam size
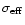 ,
with
,
with
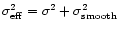 .
Its magnitude can be assessed
by considering the PSF as a Gaussian at given position and of given
width, and as smoothing filter a second Gaussian slightly displaced
from the PSF and of width slightly different from that achieving the
desired effective beam area. The result of the performed wrong
flux measurement is then proportional to the integral
.
Its magnitude can be assessed
by considering the PSF as a Gaussian at given position and of given
width, and as smoothing filter a second Gaussian slightly displaced
from the PSF and of width slightly different from that achieving the
desired effective beam area. The result of the performed wrong
flux measurement is then proportional to the integral
where 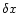 is the offset of the aperture from the correct
position and
is the offset of the aperture from the correct
position and
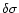 is the error in the determination of the
PSF width. The correct measurement is obtained by setting
is the error in the determination of the
PSF width. The correct measurement is obtained by setting
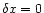 and
and
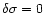 ,
and from this one obtains the fractional
flux error as a function of the two errors. The fractional flux error
,
and from this one obtains the fractional
flux error as a function of the two errors. The fractional flux error
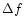 for a misalignment is
for a misalignment is
Hence, the relative flux error is better than 5% if the misalignment
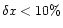 .
Similarly, for a wrong PSF width, the fractional error is
.
Similarly, for a wrong PSF width, the fractional error is
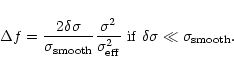 |
(A.3) |
This error is negligible if the desired effective PSF is much larger
than the intrinsic PSF of the input images, as is the case here.
A.2 Refined image alignment
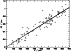 |
Figure A.1:
The
separation of a number of stars was measured both on a F336W (UV)
and a F673W (red) image of R136. This plot shows the difference in
separation between the frames, 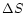 ,
plotted against the
separation on the "red'' image, S. The best-fitting straight line
is shown. ,
plotted against the
separation on the "red'' image, S. The best-fitting straight line
is shown. 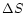 grows systematically with S, indicating a
differing scale between the frames. The slope of the line is
grows systematically with S, indicating a
differing scale between the frames. The slope of the line is
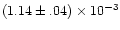 ,
the intercept with the ordinate is ,
the intercept with the ordinate is
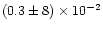 .
The slope is not changed within the
errors by forcing the line to pass through the origin. .
The slope is not changed within the
errors by forcing the line to pass through the origin. |
The two obvious ways to determine the relative shift between any two
images are measuring the positions of point sources on the various
images, or using the engineering files (also termed jitter
files) provided as part of the observing data package. If the
telescope pointing was known to be precise to better than 0
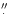 02,
we could simply rely on the commanded shifts.
The HST has a pointing repeatability within a single
telescope visit
02,
we could simply rely on the commanded shifts.
The HST has a pointing repeatability within a single
telescope visit![[*]](/icons/foot_motif.gif) of about 5 milli-arcsecond (mas). The
offsets between individual exposures are accurate to 15 mas,
leading to a total error of about 16 mas. This is already
comparable to the demanded accuracy. The situation is expected to
be worse for relating exposures in different visits, when the
telescope has been pointing elsewhere in the mean time.
Unfortunately, measuring the positions of only a few (four, in our
case) astrometric reference stars does not immediately lead to accurate
measurements of the telescope's pointing - especially since in our
case, each star lies on a different chip. The undersampling of the
telescope PSF by the WFPC2 pixels and the so-called sub-pixel
scattering of the WFPC2 detectors lead to an additional scatter of the
centroid positions of point sources, approximately uniformly
distributed between +0.25 and -0.25 pixels and in excess of
statistical uncertainties (Lallo 1998, priv. comm.). With
only a small number of centroidable point sources available, the
centroiding errors are of the same magnitude as the intrinsic pointing
errors of the telescope.
It is therefore worth considering the pointing error sources
en détail to ensure that the alignment is at the required
0
of about 5 milli-arcsecond (mas). The
offsets between individual exposures are accurate to 15 mas,
leading to a total error of about 16 mas. This is already
comparable to the demanded accuracy. The situation is expected to
be worse for relating exposures in different visits, when the
telescope has been pointing elsewhere in the mean time.
Unfortunately, measuring the positions of only a few (four, in our
case) astrometric reference stars does not immediately lead to accurate
measurements of the telescope's pointing - especially since in our
case, each star lies on a different chip. The undersampling of the
telescope PSF by the WFPC2 pixels and the so-called sub-pixel
scattering of the WFPC2 detectors lead to an additional scatter of the
centroid positions of point sources, approximately uniformly
distributed between +0.25 and -0.25 pixels and in excess of
statistical uncertainties (Lallo 1998, priv. comm.). With
only a small number of centroidable point sources available, the
centroiding errors are of the same magnitude as the intrinsic pointing
errors of the telescope.
It is therefore worth considering the pointing error sources
en détail to ensure that the alignment is at the required
0
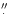 02 level
02 level![[*]](/icons/foot_motif.gif) . Alignment errors can be caused by roll or pointing errors
and less obviously by a scale difference between exposures using
different filters in the same camera. The importance of the
various alignment error sources can be estimated by considering
the effect they have on the hot spot location if the quasar images
are assumed to coincide. The hot spot is separated by 22
. Alignment errors can be caused by roll or pointing errors
and less obviously by a scale difference between exposures using
different filters in the same camera. The importance of the
various alignment error sources can be estimated by considering
the effect they have on the hot spot location if the quasar images
are assumed to coincide. The hot spot is separated by 22
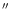 from the quasar, corresponding to about 480 PC pixels.
The roll repeatability of the HST is at the 10
from the quasar, corresponding to about 480 PC pixels.
The roll repeatability of the HST is at the 10
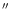 level. The
engineering data provided with HST exposures record roll angle
differences of about 6
level. The
engineering data provided with HST exposures record roll angle
differences of about 6
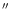 .
This is well below the rotation of
3
.
This is well below the rotation of
3
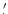 5 which would produce a 0.44 pixel difference over 480 pixels.
The telescope roll differences can thus be neglected.
The engineering files record the telescope pointing in
three-second intervals and can be used to calculate the offsets.
Their accuracy is only limited by the so-called "jitter'', vibrations
due to thermal effects. The jitter was below 10 mas in all exposures,
and below 5 mas in most. There is an additional uncertainty from the
transformation between the telescope's focal plane and the detector:
the location of a camera inside the telescope may change slightly over time
(shifts, rotations, or both). This uncertainty is irrelevant for
relative positions as long as the location and orientation of WFPC2
and the Fine Guidance Sensors (FGS, these perform the guiding
observations) inside the telescope is stable, which is the case for
the employed shifts of about 1
5 which would produce a 0.44 pixel difference over 480 pixels.
The telescope roll differences can thus be neglected.
The engineering files record the telescope pointing in
three-second intervals and can be used to calculate the offsets.
Their accuracy is only limited by the so-called "jitter'', vibrations
due to thermal effects. The jitter was below 10 mas in all exposures,
and below 5 mas in most. There is an additional uncertainty from the
transformation between the telescope's focal plane and the detector:
the location of a camera inside the telescope may change slightly over time
(shifts, rotations, or both). This uncertainty is irrelevant for
relative positions as long as the location and orientation of WFPC2
and the Fine Guidance Sensors (FGS, these perform the guiding
observations) inside the telescope is stable, which is the case for
the employed shifts of about 1
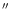 and for the timescales between
the visits.
Within a single visit, the engineering file information is used to
obtain relative offsets, with a typical 5 mas error. The values
differ from the commanded shifts by a few milli-arcseconds at most.
All of these offsets are by an integer number of PC pixels.
Between the various visits, the telescope has been pointing to a
different part of the sky. One should therefore not assume that the
relative shifts between various visits as determined from the jitter
files are as accurate as shifts within one visit. We therefore
measured the positions of the four astrometric reference stars on each
of the short exposures (in fact, one of the stars is very faint in the
UV, so the position was determined on a long exposure for this one).
The shifts determined from the four point sources' positions have a
typical standard deviation (accuracy) of 15 mas in each coordinate.
On the three visits' sum images aligned this way, the scatter of the
quasar image position is less than 5 mas and 7 mas in x and y,
respectively. This means that although the measured shifts have a
fairly large scatter, the resulting value is precise to about
10 mas. Finally, we note that the observed shifts of the stellar
positions and those obtained from the jitter files agree to better
than 0
and for the timescales between
the visits.
Within a single visit, the engineering file information is used to
obtain relative offsets, with a typical 5 mas error. The values
differ from the commanded shifts by a few milli-arcseconds at most.
All of these offsets are by an integer number of PC pixels.
Between the various visits, the telescope has been pointing to a
different part of the sky. One should therefore not assume that the
relative shifts between various visits as determined from the jitter
files are as accurate as shifts within one visit. We therefore
measured the positions of the four astrometric reference stars on each
of the short exposures (in fact, one of the stars is very faint in the
UV, so the position was determined on a long exposure for this one).
The shifts determined from the four point sources' positions have a
typical standard deviation (accuracy) of 15 mas in each coordinate.
On the three visits' sum images aligned this way, the scatter of the
quasar image position is less than 5 mas and 7 mas in x and y,
respectively. This means that although the measured shifts have a
fairly large scatter, the resulting value is precise to about
10 mas. Finally, we note that the observed shifts of the stellar
positions and those obtained from the jitter files agree to better
than 0
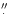 02 in all cases, with an rms value of 0
02 in all cases, with an rms value of 0
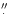 01. There
are, however, systematic differences between these and the commanded
values. Hence, we do not blindly rely on the latter.
Because of differential refraction in the MgF2 field flattener
windows employed in WFPC2 (Trauger et al. 1995), the pixel scales of
images taken through the F622W and F300W filters differ by about
0.1%. This alone is enough to eat up the alignment error budget of
0.44 pixels over 480 pixels separation. The wavelength dependence was
expected from ray-tracing studies of the WFPC2 optics. Its presence
and magnitude were experimentally confirmed by comparing archival
images
01. There
are, however, systematic differences between these and the commanded
values. Hence, we do not blindly rely on the latter.
Because of differential refraction in the MgF2 field flattener
windows employed in WFPC2 (Trauger et al. 1995), the pixel scales of
images taken through the F622W and F300W filters differ by about
0.1%. This alone is enough to eat up the alignment error budget of
0.44 pixels over 480 pixels separation. The wavelength dependence was
expected from ray-tracing studies of the WFPC2 optics. Its presence
and magnitude were experimentally confirmed by comparing archival
images![[*]](/icons/foot_motif.gif) of the star
cluster R136 taken through similar filters as those employed in the
present work (F336W and F672N) (Fig. A.1). The scale
difference has to be removed before combining the images to a spectral
index map. This was done in the following manner: the plate scale of
each image was calculated using the parameters in
Trauger et al. (1995). All images were resampled to a grid with pixel
size of 0
of the star
cluster R136 taken through similar filters as those employed in the
present work (F336W and F672N) (Fig. A.1). The scale
difference has to be removed before combining the images to a spectral
index map. This was done in the following manner: the plate scale of
each image was calculated using the parameters in
Trauger et al. (1995). All images were resampled to a grid with pixel
size of 0
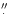 0045548, which is one tenth of the average of the
original scales, using bilinear interpolation. The result was then
binned in blocks of
0045548, which is one tenth of the average of the
original scales, using bilinear interpolation. The result was then
binned in blocks of
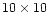 pixels to a common pixel size of
0
pixels to a common pixel size of
0
 045548. The scale of the two images is then identical to
better than 1 part in 10000.
The resampling required the use of the quasar image as common
reference point between the two filters. The QSO's position can be
determined to about 10-15 mas by centroiding routines on the unsaturated
images.
045548. The scale of the two images is then identical to
better than 1 part in 10000.
The resampling required the use of the quasar image as common
reference point between the two filters. The QSO's position can be
determined to about 10-15 mas by centroiding routines on the unsaturated
images.


Up: HST optical spectral index 3C273
Copyright ESO 2001
![]() ,
smoothed to the desired effective
beam size
,
smoothed to the desired effective
beam size
![]() ,
with
,
with
![]() .
Its magnitude can be assessed
by considering the PSF as a Gaussian at given position and of given
width, and as smoothing filter a second Gaussian slightly displaced
from the PSF and of width slightly different from that achieving the
desired effective beam area. The result of the performed wrong
flux measurement is then proportional to the integral
.
Its magnitude can be assessed
by considering the PSF as a Gaussian at given position and of given
width, and as smoothing filter a second Gaussian slightly displaced
from the PSF and of width slightly different from that achieving the
desired effective beam area. The result of the performed wrong
flux measurement is then proportional to the integral