| = | |||
| = | |||
| = | (A.1) |
In this appendix we show the expressions of the velocity components in the three systematic contributions considered in our galactic model: solar motion, differential galactic rotation and spiral arm kinematics.
A star with galactic longitude l and galactic latitude b has the
following radial and tangential velocity components owing to solar proper
motion:
We consider axisymmetric differential rotation of our galaxy, with a
rotation curve that can be developed in the solar neighbourhood as:
Lin's theory (Lin & Shu 1964; Lin et al. ; see also Rohlfs 1977) assumes a spiral potential of the
form:
where
![]() is the angular rotation velocity of
the spiral pattern, m the number of spiral arms and i the pitch angle
(for trailing spiral arms, i < 0). The phase of the spiral structure at
the Sun's position and the pitch angle can be determined from optical and
radio indicators. Nevertheless, we point out that the maximum in the
distribution of spiral arm tracers (position of the observed spiral arms)
may be shifted in relation to the minimum in the perturbation potential
(defined as
is the angular rotation velocity of
the spiral pattern, m the number of spiral arms and i the pitch angle
(for trailing spiral arms, i < 0). The phase of the spiral structure at
the Sun's position and the pitch angle can be determined from optical and
radio indicators. Nevertheless, we point out that the maximum in the
distribution of spiral arm tracers (position of the observed spiral arms)
may be shifted in relation to the minimum in the perturbation potential
(defined as
![]() ;
see Roberts 1969).
;
see Roberts 1969).
The mean peculiar velocities due to the spiral arm perturbations on the
velocity field are, in the gas approximation, the following:
![]() is the dimensionless rotation frequency of the spiral
structure, expressed in terms of the epicyclic frequency (
is the dimensionless rotation frequency of the spiral
structure, expressed in terms of the epicyclic frequency (![]() ):
):
(notice that ![]() in the region with
in the region with
![]() ,
i.e. inner to the corotation circle). Furthermore:
,
i.e. inner to the corotation circle). Furthermore:
and x is the stability Toomre's number (Toomre 1969)
defined as:
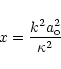 |
(A.12) |
where
![]() is the velocity dispersion of the gas
particles. Since the velocity amplitudes
is the velocity dispersion of the gas
particles. Since the velocity amplitudes
![]() and
and
![]() depend on this velocity dispersion, we introduce a
dimensionless parameter (
depend on this velocity dispersion, we introduce a
dimensionless parameter (![]() )
that relates the velocity amplitudes
of the Sun to those of the sample stars:
)
that relates the velocity amplitudes
of the Sun to those of the sample stars:
where the - sign corresponds to the inner resonance and the
+ sign to the outer one. In the region between both resonances (![]() ),
),
![]() is always positive and
is always positive and
![]() has a
sign that depends on the sign of
has a
sign that depends on the sign of ![]() .
.
The amplitude of the spiral potential can be expressed as:
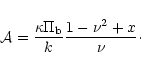 |
(A.15) |
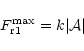 |
(A.16) |
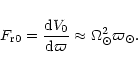 |
(A.17) |
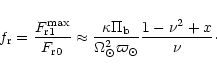 |
(A.18) |
| = | |||
| = | ![$\displaystyle \Pi_{{\rm b}} \cos \psi_\odot \left(
\cos \left[ m \left( \theta ...
...varpi_\odot}}{\tan i} \right) \right]
\sin(l + \theta) - f_\odot \sin l \right)$](/articles/aa/full/2001/24/aa1134/img258.gif) |
||
![$\displaystyle + \Pi_{{\rm b}} \sin \psi_\odot
\sin \left[ m \left( \theta -
\fr...
...t}}{\tan i} \right) \right]
\sin(l + \theta) - \Theta_{{\rm b}} \sin \psi_\odot$](/articles/aa/full/2001/24/aa1134/img259.gif) |
|||
![$\displaystyle \times \left(
\cos \left[ m \left( \theta -
\frac {\ln \frac {\va...
...varpi_\odot}}{\tan i} \right) \right]
\cos(l + \theta) - f_\odot \cos l \right)$](/articles/aa/full/2001/24/aa1134/img260.gif) |
|||
![$\displaystyle + \Theta_{{\rm b}} \cos \psi_\odot
\sin \left[ m \left( \theta -
\frac {\ln \frac {\varpi}{\varpi_\odot}}{\tan i} \right) \right]
\cos(l + \theta)$](/articles/aa/full/2001/24/aa1134/img261.gif) |
|||
![$\displaystyle = \Pi_{{\rm b}} \cos \psi_\odot \left(
\cos \left[ m \left( \thet...
...}}{\tan i} \right) \right]
\cos (l {+} \theta {-} f_\odot \cos l \right) \sin b$](/articles/aa/full/2001/24/aa1134/img264.gif) |
|||
![$\displaystyle + \Pi_{{\rm b}} \sin \psi_\odot
\sin \left[ m \left(\theta -
\fra...
...n \frac {\varpi}{\varpi_\odot}}{\tan i} \right) \right]
\cos(l + \theta) \sin b$](/articles/aa/full/2001/24/aa1134/img265.gif) |
|||
![$\displaystyle + \Theta_{{\rm b}} \sin \psi_\odot \left(
\cos \left[ m \left( \t...
...}}{\tan i} \right) \right]
\sin(l {+} \theta) {-} f_\odot \sin l \right) \sin b$](/articles/aa/full/2001/24/aa1134/img266.gif) |
|||
![$\displaystyle - \Theta_{{\rm b}} \cos \psi_\odot
\sin \left[ m \left(\theta -
\...
... \frac {\varpi}{\varpi_\odot}}{\tan i} \right) \right]
\sin(l + \theta) \sin b.$](/articles/aa/full/2001/24/aa1134/img267.gif) |
(A.19) |
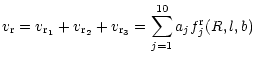 |
|||
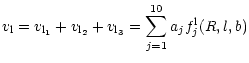 |
|||
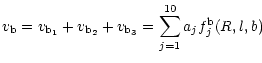 |
(A.20) |
where the constants aj contain combinations of the kinematic
parameters that we wish to determine:
and
fji(R,l,b) are functions of the heliocentric distance
and the galactic longitude and latitude:
With regard to the free parameters of our model, different values for m,
i,
![]() ,
,
![]() were considered (see Sect.
7).
were considered (see Sect.
7).
Copyright ESO 2001