7 Discussion

7.1 Galactic rotation curve

A difference in the A Oort constant of approximately 3 km s^-1 kpc^-1 between solutions for O and B stars and Cepheids with short cosmic scale distances is obtained, whereas large cosmic scale provides an intermediate value:

$$A^{\rm OB} \approx 13.7{-}13.8 {\rm\; km \; s}^{-1} {\rm\;~kpc}^{-1}$$

$$A^{\rm Cep}_{{\rm Short}} \approx 16.6{-}16.9 {\rm\; km \; s}^{-1} {\rm\;~kpc}^{-1}$$

$$A^{\rm Cep}_{{\rm Large}} \approx 14.9{-}15.1 {\rm\; km \; s}^{-1} {\rm\;~kpc}^{-1}.$$ (12)

As can be seen in Appendix B, these differences cannot be explained by the observational constraints present in both samples. A similar discrepancy was found by Frink et al. (1996), who derived $A = 14.0 \pm 1.2$ km s^-1 kpc^-1 from a sample of O and B stars, and $A = 15.8 \pm 1.6$ km s^-1 kpc^-1 from a sample of Cepheids (in both cases the authors only considered those stars with a heliocentric distance of less than 1 kpc). Nonetheless, our values for Cepheids do not reach the higher values obtained by Glushkova et al. (1998; $A = 19.5 \pm 0.5$ km s^-1 kpc^-1), Mishurov et al. (1997; $A = 20.9 \pm 1.2$ km s^-1 kpc^-1), Mishurov & Zenina (1999; $A = 18.8 \pm 1.3$ km s^-1 kpc^-1) and Lépine et al. (2001; $A = 17.5 \pm 0.8$ km s^-1 kpc^-1). Pont et al. (1994) and Metzger et al. (1998), from radial velocities of Cepheid stars, found values of $A = 15.9 \pm 0.3$ km s^-1 kpc^-2 and $A = 15.5 \pm 0.4$ km s^-1 kpc^-2, respectively. More recently, and using proper motions and distance calibration from Hipparcos data on Cepheid stars, Feast & Whitelock (1997) found a value of $A = 14.8 \pm 0.8$ km s^-1 kpc^-1. Using a similar sample, Feast et al. (1998) found $A = 15.1 \pm 0.3$ km s^-1 kpc^-1 from radial velocities. As we have mentioned in Sect. 6, we found good coherence for radial velocity, proper motion and combined solutions for both cosmic distance scales.

An attempt to explain these discrepancies was made by Olling & Merrifield (1998), who studied the variation of the A and B Oort functions and found that they significantly differ from the general $\sim$ $\Theta(\varpi)/\varpi$ dependence expected for a nearly flat rotation curve. Inside the solar circle, the value of A rises to 18 km s^-1 kpc^-1 for $\Delta\varpi = \varpi - \varpi_\odot \approx -0.5$ kpc, disminishes to 16 km s^-1 kpc^-1 for $\Delta\varpi \approx -1.2$ kpc, and rises continuously for  kpc, to 19 km s^-1 kpc^-1 for $\Delta\varpi \approx -2$ kpc (see Fig. 3 in Olling & Merrifield 1998). Contrary to that, beyond the solar circle A decreases to 10-12 km s^-1 kpc^-1, maintaining this value in the interval  kpc. Although Ais a local parameter, describing the local shape of the rotation curve, Olling & Merrifield already pointed out that the discrepancies in the results published in the literature may be produced by their dependence on the galactocentric distance. Our O and B stars are distributed along all the galactic longitudes, whereas the Cepheids are predominantly concentrated inside the solar circle, with a peak in the spatial distribution for $\Delta\varpi \approx -0.6$ kpc corresponding to the Sagittarius-Carina arm (see Figs. 1 and 2). For O and B stars we found a classical value of $A \approx 14$ km s^-1 kpc^-1 (a value between 10-12 and 16-18 km s^-1 kpc^-1), whereas for Cepheids a value $A \approx 15$-17 km s^-1 kpc^-1 (depending on the PL relation considered) was derived, in agreement with Olling & Merrifield's assumptions.

From the results obtained in Appendix B, we would expect uncertainties in the second-order term of the rotation curve of $\approx$1.0 km s^-1 kpc^-2 for O and B stars and $\approx$0.5 km s^-1 kpc^-2 in the case of Cepheids. Taking this and the results in Table 3 into account, we can state that $b_{\rm r}$does not differ from a null value more than 2 km s^-1 kpc^-2. Pont et al. (1994) found a value $b_{\rm r} = -1.7 \pm 0.2$ km s^-1 kpc^-2, whereas Feast et al. () found $b_{\rm r} = -1.6 \pm 0.2$ km s^-1 kpc^-2, both using radial velocities of Cepheid stars (the latter with a Hipparcos distance calibration). A large positive value was found by Lépine et al. (2001), who derived $b_{\rm r} = 5.0 \pm 1.0$ km s^-1 kpc^-2 from their sample of Cepheid stars. As we will see in Sect. 7.2, these authors also found a large value for the amplitude of the velocity component in the galactic rotation direction due to the spiral potential ( $\Theta _{\rm b}$). Without specific simulations, considering both their observational data and resolution procedure, it is difficult to guess how the correlations between both parameters can affect their determination.

  
7.2 Spiral structure

Appendix B demonstrates that the available observational data allow the characterization of the galactic spiral structure, though the biases and uncertainties on the parameters have to be taken into account in the interpretation of the results. Furthermore, we realized that it is very difficult to establish the correct number of spiral arms of the Galaxy.

A first remarkable result is the fairly good coherence obtained for the phase of the spiral structure at the Sun's position $\psi _\odot$ when using different free parameters (cases A, D) or different samples compared to the great discrepancies found in the literature (see below). We take into consideration that $\Pi _{\rm b}$, $\Theta _{\rm b}$ and $f_\odot$ depend on the cosmic dispersion and so they do not have the same value for O and B stars and Cepheids.

Figure 4: Star distribution in the X-Y galactic plane for O and B stars (filled circles) with 0.6 < R < 2 kpc and Cepheids (empty circles) with 0.6 < R < 4 kpc (short cosmic scale distances). Spiral arms were drawn considering $\psi _\odot = 330\hbox {$^\circ $ }$. Dotted lines show the center of the spiral arms ( $\psi = 0\hbox {$^\circ $ }$) and dashed lines draw their approximate edges ( $\psi = \pm 90\hbox {$^\circ $ }$). Looking at this figure we must have in mind the possible drift between the position of the optical tracers in the spiral arms (i.e., our young stars) and the minimum of the spiral potential ( $\psi = 0\hbox {$^\circ $ }$).

From Fig. 2, and assuming that Cepheids fairly trace the center of the Sagittarius-Carina arm, we can infer a value of $\psi_\odot \approx$ 250 $\hbox{$^\circ$ }$ (the center of the inner visible spiral arm -the Sagittarius-Carina arm- at about 1 kpc from the Sun), depending on the exact value of the interarm distance. Nevertheless, the density wave theory predicts that the center of the visible arm (traced by its young stars) does not coincide with the position of the spiral potential minimum (Roberts 1969, 1970). We must bear in mind that the kinematically derived value for $\psi _\odot$ informs us about the position of the Sun with respect this potential minimum, not with respect the visible arm. In Table 3 we found values inside the interval:

$$\psi_\odot \approx 284{-}20\hbox{$^\circ$ }.$$ (13)

We take into consideration that in the minimum of the spiral potential (near the center of an arm) $\psi = 0\hbox {$^\circ $ }$, whereas in the inner edge of the arm $\psi \approx 90\hbox{$^\circ$ }$ and in the outer edge $\psi \approx -90\hbox{$^\circ$ }= 270\hbox{$^\circ$ }$. In the case of the phase of the spiral structure at the Sun's position we expect a bias of $\Delta \psi_\odot = \psi_\odot^{{\rm obtained}} - \psi_\odot^{{\rm real}} \approx 20\hbox{$^\circ$ }$ for O and B stars and $\Delta \psi_\odot \approx 0\hbox{$^\circ$ }$ for Cepheids, with uncertainties of $\approx$25$^\circ$and $\approx$75$^\circ$, respectively (see Appendix B). These high uncertainties can explain the range of values obtained. According to the value found for $\psi _\odot$, the Sun is located between the center and the outer edge of an arm, nearer to the former (see Fig. 4).

Our result stands in apparent contradiction to the classical mapping of the spiral structure tracers (Schmidt-Kaler 1975; Elmegreen 1985), which locates the Sun in a middle position between the inner arm (Sagittarius-Carina arm) and the outer one (Perseus arm), that is, $\psi_\odot \approx 180\hbox{$^\circ$ }$. The local arm (Orion-Cygnus arm) is normally considered as a local spur rather than a real arm. In our model, as we supposed an interarm distance of approximately 3 kpc, the local arm is also considered a local spur (see Sect. 3.2). But the value we obtained for $\psi _\odot$differs significantly from $180\hbox{$^\circ$ }$. If we consider a difference of 30- $100\hbox{$^\circ$ }$ between the optical tracers and the potential minimum of the spiral arm, we notice that our $\psi _\odot$ value is in good agreement with the picture of the spiral structure that emerges from the spatial distribution of stars in Fig. 4, with the inner spiral arm at approximately 1 kpc from the Sun. A similar result was obtained by Mel'nik et al. (1998), who found that nearly 70% of the stars in the OB associations of the Sagittarius-Carina arm have a residual motion (after correcting their heliocentric velocities for solar motion and galactic rotation) in the direction opposite to the galactic rotation, as one would expect for those stars between the inner edge and the center of the arm. Then, they also found a shift between the optical position of the visible arm (traced by young stars) and the minimum of the spiral potential. Therefore, from our results we conclude that the Sun is placed relatively near the potential minimum of the Sagittarius-Carina arm, and the Perseus arm is located far away, at about 2.5 kpc from the Sun.

Our range of values for $\psi _\odot$ includes that obtained by Crézé & Mennessier (1973) from a sample of O-B3 stars, $\psi_\odot = 352 \pm 30\hbox{$^\circ$ }$. Later, Mennessier & Crézé (1975) found from a sample of O-B3 stars a value of $\psi_\odot \approx 90\hbox{$^\circ$ }$, which locates the Sun near the inner edge of an arm. Other authors obtained contradictory results. Gómez & Mennessier (1977) found the Sun's position near the edge of an arm from several samples of stars from FK4 and FK4 Supplement Catalogues. Byl & Ovenden (1978) and Comerón & Torra (1991) obtained values of $\psi_\odot = 165 \pm 1\hbox{$^\circ$ }$and $\psi_\odot = 135 \pm 18\hbox{$^\circ$ }$ respectively, from samples of O and B stars. Mishurov et al. (1997) found $\psi_\odot = 290 \pm 16\hbox{$^\circ$ }$ from a sample of Cepheid stars with radial velocities. Mishurov & Zenina (1999) found $\psi_\odot = 322 \pm 9\hbox{$^\circ$ }$ (supposing m = 2 and $\varpi_\odot = 7.5$ kpc), from the same sample of Cepheid stars, but also including the Hipparcos proper motions. When these authors supposed m = 4 they found $\psi_\odot = 340 \pm 9\hbox{$^\circ$ }$. More recently, Rastorguev et al. (2001) found $\psi_\odot = 274 \pm 22\hbox{$^\circ$ }$ from a sample of 55 open clusters younger than 40 Myr and 67 Cepheids with periods smaller than 9 days, all of them at R < 4 kpc. We can see that there is poor agreement between the results published in the literature, though the last ones (the only ones with Hipparcos data) are all included in our range of possible values for $\psi _\odot$.

The velocity amplitudes due to the spiral perturbation obtained are less than 4 km s^-1 for O and B stars ( $\Pi_{{\rm b}} \approx 3$ km s^-1, $\Theta_{{\rm b}} \approx$ 2-3 km s^-1) and 6 km s^-1for Cepheid stars ( $\Pi_{{\rm b}} \approx -1$-1 km s^-1, $\Theta_{{\rm b}} \approx$ 2-6 km s^-1). The difference between results for O and B stars and Cepheids is explained by Lin's theory as a result of their slight dependence on the galactocentric distance and the different cosmic dispersion for both samples. Mishurov et al. (1997) found $\Pi_{{\rm b}} = 6.3 \pm 2.4$ km s^-1 and $\Theta_{{\rm b}} = 4.4 \pm 2.4$ km s^-1 from their radial velocity data of Cepheid stars within 4 kpc from the Sun, supposing a 2-armed spiral pattern. Mel'nik et al. (1999) found $\Pi_{{\rm b}} = 6.4 \pm 1.2$ km s^-1 and $\Theta_{{\rm b}} = 2.4 \pm 1.2$ km s^-1 from Cepheids within 3 kpc from the Sun. Mishurov & Zenina (1999) found $\Pi_{{\rm b}} = 3.3 \pm 1.6$ km s^-1 and $\Theta_{{\rm b}} = 7.9 \pm 2.0$ km s^-1for m = 2 and $\Pi_{{\rm b}} = 3.5 \pm 1.7$ km s^-1 and $\Theta_{{\rm b}} = 7.5 \pm 1.8$ km s^-1 for m = 4. From the same sample, Lépine et al. (2001) found $\Pi_{{\rm b}}^{m=2} = 0.4 \pm 3.0$ km s^-1, $\Theta_{{\rm b}}^{m=2} = 14.0 \pm 3.0$ km s^-1 and $\Pi_{{\rm b}}^{m=4} = 0.8 \pm 3.3$ km s^-1, $\Theta_{{\rm b}}^{m=4} = 10.9 \pm 2.9$ km s^-1. Their 2+4-armed model yields large values for $\Theta _{\rm b}$, implying a large value for the ratio between the spiral potential and the axisymmetric galactic field, much greater than that 5-10% normally accepted. According to the results obtained in Appendix B, the present observational uncertainties, biases and the correlations involved in the resolution procedure cannot completely explain the discrepancies among the values found in the literature. They can be attributed to our poor knowledge of the real wave harmonic structure of the galactic spiral pattern or to the approximation performed in the linear density-wave theory.

The derived angular rotation velocity of the spiral pattern is:

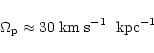$$\Omega_{{\rm p}} \approx 30 {\rm\; km \; s}^{-1} {\rm\;~kpc}^{-1}$$ (14)

though there is a great dispersion around this value in our results from different samples and cases (dispersion of 2-7 km s^-1 kpc^-1, but up to 15 km s^-1 kpc^-1 in one extreme case). This is an expected dispersion, taking into account the results obtained in Appendix B (standard deviation of 2-5 km s^-1 kpc^-1 for O and B stars, but up to 15 km s^-1 kpc^-1 for $\psi_\odot \approx 270\hbox{$^\circ$ }$; for Cepheids dispersions are higher, of about 10-20 km s^-1 kpc^-1). Such a value places the Sun very near the corotation circle and is not in agreement with the classical $\Omega_{{\rm p}} \approx 13.5$ km s^-1 kpc^-1 proposed by Lin et al. (1969). Nevertheless, other studies show results similar to ours. Avedisova (1989) obtained $\Omega_{{\rm p}} = 26.8 \pm 2$ km s^-1 kpc^-1 from the spatial distribution of young objects of different ages in the Sagittarius-Carina arm. More recently, Amaral & Lépine (1997), working with a selection of young members of the open cluster catalogue by Mermilliod (1986), obtained a value of $\Omega_{\rm p} \approx$ 20-22 km s^-1 kpc^-1. Mishurov et al. (1997) and Mishurov & Zenina () used their sample of Cepheid stars and found $\Omega_{{\rm p}} = 28.1 \pm 2.0$ km s^-1 kpc^-1 and $\Omega_{{\rm p}} \approx 27.7$ km s^-1 kpc^-1, respectively. Lépine et al. () found $\Omega_{{\rm p}}^{m=2} \approx \Omega_{{\rm p}}^{m=4} \approx 26.5$ km s^-1 kpc^-1 from their sample of Cepheid stars. Rastorguev et al. (2001) thought that the evaluation of $\Omega _{{\rm p}}$ from kinematical data alone cannot be resolved. But our simulations (see Appendix B) seem to indicate that, at least, the tendency to find high values of $\Omega _{{\rm p}}$ is confirmed, though there is still an uncertainty of about 5-10 km s^-1 kpc^-1 in its value. These large values for $\Omega _{{\rm p}}$ can explain in a natural way the presence of a gap in the galactic gaseous disk (see Kerr 1969 and Burton 1976 for observational evidences and Lépine et al. 2001 for simulated results), since they placed the Sun near the corotation circle, where the gas is pumped out under the influence of the spiral potential.

7.3 The K-term

In relation to the K-term, we found good agreement between both O and B stars and Cepheids. A value of $K \approx -$(1-3) km s^-1 kpc^-1is found in all cases, confirming an apparent compression of the solar neighbourhood of up to 3-4 kpc. In our opinion, what most clearly proves the existence of a non-null value of K is that it is independently found from the samples of O and B stars and Cepheids, which have a very different spatial distribution, an independent distance estimation and a different way of deriving their radial velocities. As we can see comparing Tables 2 and 3, the inclusion of the K-term does not substantially modify the other model parameters derived by least squares fit.

It is very difficult to find in the literature other estimations of K at these large heliocentric distances, since in the majority of cases authors consider an axisymmetric rotation curve. But some authors have pointed out the persistence of a residual in the radial velocity equations. Comerón & Torra (1994) found $K = -1.9 \pm 0.5$ km s^-1 kpc^-1 from O-B5.5 stars and $K = -1.3 \pm 0.9$ km s^-1 kpc^-1from B6-A0 stars with R < 1.5 kpc. The radial velocity residual for Cepheids was first recognised by Stibbs (1956). Pont et al. (1994) studied three possible origins for it: a statistical effect, an intrinsic effect in the measured radial velocities for Cepheids ($\gamma$-velocities) and a real dynamical effect. They finally suggested that it could be due to a non-axisymmetric motion produced by a central bar of $\approx$5 kpc in extent. Metzger et al. (1998) found a residual of $\approx-$3 km s^-1 for a sample of Cepheids when considering an axisymmetric galactic rotation. They concluded that it might be due to the influence of spiral structure, not included in their model. However, in the present work we found a non-null K value even taking into account spiral arm kinematics. An understanding of the physical explanation of the K-term requires further study.