| (3) |
We propose an extension of the bidimensional model previously applied for
radial velocities by Comerón & Torra (1991). In our
model we considered the systematic velocity components:
where subindex 1 refers to the solar motion contribution,
subindex 2 to differential galactic rotation and subindex 3 to spiral arm
kinematics, respectively (see Appendix A). Solar motion is
expressed through the three components of the Sun's velocity in galactic
coordinates (
![]() ). Galactic rotation curve was
developed up to second-order approximation,
). Galactic rotation curve was
developed up to second-order approximation, ![]() and
and
![]() being the first- and second-order terms, respectively:
being the first- and second-order terms, respectively:
where we show the relationship between ![]() and the
A Oort constant. B Oort constant can be derived from:
and the
A Oort constant. B Oort constant can be derived from:
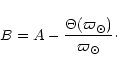 |
(5) |
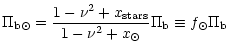 |
|||
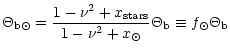 |
(6) |
where ![]() is the dimensionless rotation frequency of the
spiral structure and x is the stability Toomre's number (Toomre
1969), which depends on the velocity dispersion of the considered
stars (see details in Appendix A). The inclusion of
is the dimensionless rotation frequency of the
spiral structure and x is the stability Toomre's number (Toomre
1969), which depends on the velocity dispersion of the considered
stars (see details in Appendix A). The inclusion of ![]() is
new with regard to the model proposed by Comerón & Torra ().
is
new with regard to the model proposed by Comerón & Torra ().
Equation (3) can be expressed as:
where the constants aj contain combinations of the kinematic
parameters we wish to determine (![]() ,
,
![]() ,
,
![]() ,
,
![]() ,
,
![]() ,
,
![]() ,
,
![]() ,
,
![]() and
and ![]() )
and
fji(R,l,b) are functions of
the heliocentric distance and the galactic longitude and latitude (see
Eqs. (A.21) and (A.22)).
)
and
fji(R,l,b) are functions of
the heliocentric distance and the galactic longitude and latitude (see
Eqs. (A.21) and (A.22)).
A 2-armed Galaxy was the first proposed view for our stellar system,
mainly derived from HI and HII observations, but also from the spatial
distribution of supergiant stars and other bright objects. These classical
studies show the existence of at least two arms inside the solar circle
(the Sagittarius-Carina or -I arm and the Norma-Scutum or -II arm),
one local arm (Orion-Cygnus or 0 arm) and one external arm (Perseus or
+I arm). The Orion-Cygnus arm seems to be a local spur (Bok 1958).
Lin et al. (1969) proposed a galactic system with 2 main
spiral arms, where the Norma-Scutum and the Perseus arms are two segments
of the same arm. By taking into account the interarm distance between the
Sagittarius-Carina and the Perseus arms, these authors deduced a pitch
angle of -6![]() .
But, as early as the mid-70s, Georgelin & Georgelin
(1976) proposed a 4-armed galactic system with a pitch
angle of
.
But, as early as the mid-70s, Georgelin & Georgelin
(1976) proposed a 4-armed galactic system with a pitch
angle of
![]() from a study of the spatial distribution of HII
regions. However, Bash (1981) examined this 4-armed model and found
that a 2-arm pattern predicts HII regions in the same direction and with
the same radial velocities as those used by Georgelin & Georgelin
(1976), provided that dispersion velocities were
considered.
from a study of the spatial distribution of HII
regions. However, Bash (1981) examined this 4-armed model and found
that a 2-arm pattern predicts HII regions in the same direction and with
the same radial velocities as those used by Georgelin & Georgelin
(1976), provided that dispersion velocities were
considered.
In some recent papers several authors have also called this classical view
in question. Vallée (1995) reviewed the subject of the
determination of the pitch angle and the number of spiral arms and
concluded that the Galaxy has a pitch angle of
![]() and
that, taking into account the observed interarm distance, it would be a
system of 4 spiral arms. This is also the opinion expressed by Amaral &
Lépine (1997), who, fitting the galactic rotation curve
to a mass model of the Galaxy, found an autoconsistent solution with a
system of 2 + 4 spiral arms (2 arms for 2.8
and
that, taking into account the observed interarm distance, it would be a
system of 4 spiral arms. This is also the opinion expressed by Amaral &
Lépine (1997), who, fitting the galactic rotation curve
to a mass model of the Galaxy, found an autoconsistent solution with a
system of 2 + 4 spiral arms (2 arms for 2.8
![]() 13 kpc and 4 arms
for
13 kpc and 4 arms
for
![]() kpc, with the Sun placed at
kpc, with the Sun placed at
![]() kpc) and a pitch angle of
kpc) and a pitch angle of
![]() .
Englmaier & Gerhard
(1999) used the COBE NIR luminosity distribution and
connected it with the kinematic observations of HI and molecular gas in
l-v diagrams. They found a 4-armed spiral pattern between the
corotation of the galactic bar and the solar circle. Drimmel
(2000) found that the galactic plane emission in the K band is
consistent with a 2-armed structure, whereas the 240
.
Englmaier & Gerhard
(1999) used the COBE NIR luminosity distribution and
connected it with the kinematic observations of HI and molecular gas in
l-v diagrams. They found a 4-armed spiral pattern between the
corotation of the galactic bar and the solar circle. Drimmel
(2000) found that the galactic plane emission in the K band is
consistent with a 2-armed structure, whereas the 240 ![]() m emission from
dust is compatible with a 4-armed pattern. In a recent work, Lépine et al. (2001) analyzed the kinematics of a sample of Cepheid
stars and found the best fit for a model with a superposition of 2+4
spiral arms. Contrary to the model by Amaral & Lépine (), Lépine et al. allowed the phase of both spiral patterns to be
independent, deriving pitch angles of approximately
m emission from
dust is compatible with a 4-armed pattern. In a recent work, Lépine et al. (2001) analyzed the kinematics of a sample of Cepheid
stars and found the best fit for a model with a superposition of 2+4
spiral arms. Contrary to the model by Amaral & Lépine (), Lépine et al. allowed the phase of both spiral patterns to be
independent, deriving pitch angles of approximately
![]() and
and
![]() for m=2 and m=4, respectively. They argued that this spiral
pattern is in good agreement with the l-v diagrams obtained from
observational HII data, though they admit that pure 2-armed model produces
similar results. In the visible spiral structure of the Galaxy derived by
Lépine et al. (see their Fig. 3) the Orion-Cygnus or local arm is seen
as a major structure with a small pitch angle. In contrast, Olano
(2001) proposed that the local arm is an elongated structure of
only 4 kpc of length and a pitch angle of about
for m=2 and m=4, respectively. They argued that this spiral
pattern is in good agreement with the l-v diagrams obtained from
observational HII data, though they admit that pure 2-armed model produces
similar results. In the visible spiral structure of the Galaxy derived by
Lépine et al. (see their Fig. 3) the Orion-Cygnus or local arm is seen
as a major structure with a small pitch angle. In contrast, Olano
(2001) proposed that the local arm is an elongated structure of
only 4 kpc of length and a pitch angle of about
![]() (in better
agreement with the observational determinations of the inclination of the
local arm found in the literature) formed from a supercloud about 100 Myr
ago, when it entered into a major spiral arm.
(in better
agreement with the observational determinations of the inclination of the
local arm found in the literature) formed from a supercloud about 100 Myr
ago, when it entered into a major spiral arm.
In the case of the galactocentric distance of the Sun and the circular
velocity at the Sun's position there are also some inconsistencies among
the different values found in the literature. In 1986, the IAU adopted the
values
![]() 8.5 kpc and
8.5 kpc and
![]() km s-1 (Kerr & Lynden-Bell 1986). Recently, several
authors have found values of nearly 7.5 kpc for
km s-1 (Kerr & Lynden-Bell 1986). Recently, several
authors have found values of nearly 7.5 kpc for
![]() (Racine &
Harris 1989; Maciel 1993). A complete review was
done by Reid (1993), who concluded that the most suitable value
seems to be
(Racine &
Harris 1989; Maciel 1993). A complete review was
done by Reid (1993), who concluded that the most suitable value
seems to be
![]() kpc. In kinematic studies there
are serious discrepancies between different authors. Metzger et al.
(1998) found
kpc. In kinematic studies there
are serious discrepancies between different authors. Metzger et al.
(1998) found
![]() kpc and
kpc and
![]() km s-1, whereas Feast et al.
(1998) found
km s-1, whereas Feast et al.
(1998) found
![]() kpc (both from
radial velocities of Cepheid stars). Glushkova et al. () found
kpc (both from
radial velocities of Cepheid stars). Glushkova et al. () found
![]() kpc from a combined sample
including open clusters, red supergiants and Cepheids. Olling &
Merrifield (1998) calculated mass models for the Galaxy
and concluded that a consistent picture only emerges when considering
kpc from a combined sample
including open clusters, red supergiants and Cepheids. Olling &
Merrifield (1998) calculated mass models for the Galaxy
and concluded that a consistent picture only emerges when considering
![]() kpc and
kpc and
![]() km s-1. This value for the galactocentric distance of the Sun is in very
good agreement with the only direct distance determination (
km s-1. This value for the galactocentric distance of the Sun is in very
good agreement with the only direct distance determination (
![]() kpc), which was made employing proper motions of H2O
masers (Reid 1993).
kpc), which was made employing proper motions of H2O
masers (Reid 1993).
In the view of all that, we decided to derive the kinematic parameters of
our model from different combinations of the free parameters involved. On
the one hand, concerning spiral structure, two models of the Galaxy were
considered: a first model with m = 2 and
![]() ,
and a second one
with m = 4 and
,
and a second one
with m = 4 and
![]() .
Both models are consistent with an
interarm distance of about 2.5-3 kpc, depending on the adopted value for
the distance from the Sun to the galactic center. On the other hand,
concerning the galactocentric distance of the Sun and the circular
velocity at the Sun's position, two different cases were also taken into
account: a first one with
.
Both models are consistent with an
interarm distance of about 2.5-3 kpc, depending on the adopted value for
the distance from the Sun to the galactic center. On the other hand,
concerning the galactocentric distance of the Sun and the circular
velocity at the Sun's position, two different cases were also taken into
account: a first one with
![]() kpc and
kpc and
![]() km s-1, and a second one with
km s-1, and a second one with
![]() kpc and
kpc and
![]() km s-1. In
both cases, the angular rotation velocity at the Sun's position is
km s-1. In
both cases, the angular rotation velocity at the Sun's position is
![]() km s-1 kpc-1.
km s-1 kpc-1.
Copyright ESO 2001