| = | 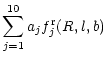 |
||
| = | 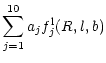 |
||
| = | 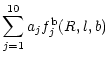 |
(8) |
We determined the kinematic parameters of the galactic model via least
squares fit from the equations:
where
![]() is the radial velocity of the star in
km s-1, k = 4.741 km yr (s pc
is the radial velocity of the star in
km s-1, k = 4.741 km yr (s pc
![]() )-1, R is the
heliocentric distance of the star in pc,
)-1, R is the
heliocentric distance of the star in pc,
![]() and
and
![]() are the proper motion in galactic longitude and
latitude of the star in
are the proper motion in galactic longitude and
latitude of the star in
![]() yr-1 and b the galactic
latitude. To derive the parameters aj, an iterative scheme
extensively explained in Fernández (1998) was followed.
yr-1 and b the galactic
latitude. To derive the parameters aj, an iterative scheme
extensively explained in Fernández (1998) was followed.
The weight system was chosen as:
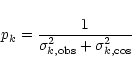 |
(9) |
where
![]() are the individual observational
errors in each velocity component of the star, calculated by taking into
account the correlations between the different variables provided by the
Hipparcos Catalogue, and
are the individual observational
errors in each velocity component of the star, calculated by taking into
account the correlations between the different variables provided by the
Hipparcos Catalogue, and
![]() is the projection of the
cosmic velocity dispersion ellipsoid in the direction of the velocity
component considered (see Paper I).
is the projection of the
cosmic velocity dispersion ellipsoid in the direction of the velocity
component considered (see Paper I).
To check the quality of the least squares fits we considered the ![]() statistics for N - M degrees of freeedom, defined as:
statistics for N - M degrees of freeedom, defined as:
![\begin{displaymath}\chi^2 = \sum_{k=1}^{N}
\frac {\left[ y_k - y(x_k; a_1,...,a...
... \right]^2}
{\sigma_{k,{\rm obs}}^2 + \sigma_{k,{\rm obs}}^2}
\end{displaymath}](/articles/aa/full/2001/24/aa1134/img96.gif) |
(10) |
where xk are the independent data (sky coordinates and
distances), yk the dependent data (radial and tangential velocity
components), N the number of equations and M number of parameters to
be fitted. According to Press et al. (1992), if the
uncertainties (cosmic dispersion and observational errors) are
well-estimated, the value of ![]() for a moderately good fit would be
for a moderately good fit would be
![]() ,
with an uncertainty of
,
with an uncertainty of
![]() .
.
As we did in Paper I, to eliminate the possible outliers present in the
sample due to both the existence of high residual velocity stars (Royer
1997) or stars with unknown large observational errors, we
rejected those equations with a residual larger than 3 times the root mean
square residual of the fit (computed as
![]() )
and recomputed a new set of parameters.
)
and recomputed a new set of parameters.
Copyright ESO 2001