In this section, it will be investigated how the linewidth correction for turbulent motion can be used to match the finally corrected global HI linewidths to the actual rotational velocities measured from the rotation curves.
After the correction for instrumental resolution, the profile widths
are generally corrected for broadening due to turbulent motions of the
HI gas by applying TFq's formula
![\begin{eqnarray*}W^2_{R,l} = W^2_l + W^2_{t,l} \left[ 1 - 2 {\rm e}^{-\left(\fra...
...ft[1 - {\rm e}^{-\left(\frac{W_l}{W_{c,l}}\right)^2} \right] \\
\end{eqnarray*}](/articles/aa/full/2001/18/aa10469/img151.gif)
The generally adopted values for Wc,l are
![]() and
and
![]() .
The more important
values of Wt,l, however, have been subject of some debate among various
authors. With our new HI synthesis data we can give a meaningful
contribution to this debate.
.
The more important
values of Wt,l, however, have been subject of some debate among various
authors. With our new HI synthesis data we can give a meaningful
contribution to this debate.
Bottinelli et al. (1983) came up with an empirical
approach, based on a minimization of the scatter in the TF-relation.
They assumed an anisotropic velocity dispersion of the HI gas of
![]() and a velocity dispersion
perpendicular to the plane of
and a velocity dispersion
perpendicular to the plane of
![]() .
They determined the
values of kl by minimizing the scatter in the TF-relation and found
k20=1.89 and
k50=0.71, indicating deviations from a Gaussian
distribution (broader wings). Due to the assumed velocity anisotropy,
Wt,l has become a function of inclination angle and varies in the
range
45<Wt,20<57 and
17<Wt,50<21 for inclinations
ranging between
.
They determined the
values of kl by minimizing the scatter in the TF-relation and found
k20=1.89 and
k50=0.71, indicating deviations from a Gaussian
distribution (broader wings). Due to the assumed velocity anisotropy,
Wt,l has become a function of inclination angle and varies in the
range
45<Wt,20<57 and
17<Wt,50<21 for inclinations
ranging between
![]() .
.
The same value of
k20=1.89 was adopted by TFq but they
assumed an isotropic velocity dispersion of
![]() and consequently advocate
and consequently advocate
![]() ,
independent of inclination.
They did not address the situation at the 50% level.
,
independent of inclination.
They did not address the situation at the 50% level.
Fouqué et al. (1990) also assumed isotropy but adopted
![]() .
They determined kl in a more direct way by
comparing the corrected line width to the observed maximum rotational
velocity
.
They determined kl in a more direct way by
comparing the corrected line width to the observed maximum rotational
velocity
![]() as derived from HI velocity
fields. They found
k20=1.96 and
k50=1.13, indicating a
near-Gaussian distribution, contrary to the findings of Bottinelli
et al. Consequently, Fouqué et al. advocate the much larger values of
as derived from HI velocity
fields. They found
k20=1.96 and
k50=1.13, indicating a
near-Gaussian distribution, contrary to the findings of Bottinelli
et al. Consequently, Fouqué et al. advocate the much larger values of
![]() and
and
![]() respectively.
respectively.
A similar procedure was followed by Broeils (1992) using a
sample of 21 galaxies with well defined HI velocity fields. Broeils made
no a priori assumptions about the intrinsic velocity dispersion and did
not decouple kl and ![]() .
He did, however, recognize that
.
He did, however, recognize that
![]() may exceed
may exceed
![]() and he determined for each galaxy the
values of
and he determined for each galaxy the
values of
![]() and
and
![]() for which the
differences
for which the
differences
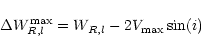
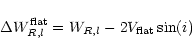
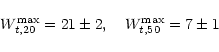
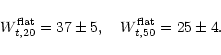
Finally, Rhee (1996a) performed the same investigation using 28
galaxies, most of them in common with Broeils' (1992)
sample. Not surprisingly, he found
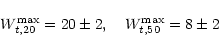
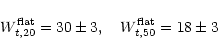
Here, with our new and independent dataset, we follow the same strategy
as Broeils and Rhee by investigating which values of Wt,l allow an
accurate retrieval of ![]() and
and
![]() from the broadened global profile. For
this purpose we will only consider those 22 galaxies in our Ursa Major
sample that show a flat part in their rotation curves (with a
significant amount of HI gas) and that are free from a major change in
inclination angle. Of these 22, there are 6 galaxies with
from the broadened global profile. For
this purpose we will only consider those 22 galaxies in our Ursa Major
sample that show a flat part in their rotation curves (with a
significant amount of HI gas) and that are free from a major change in
inclination angle. Of these 22, there are 6 galaxies with
![]() .
Note
that both Broeils and Rhee used Bottinelli et al.'s prescription to
correct for instrumental broadening which we are forced to adopt here to
ensure a valid comparison between their and our results. We calculated
the values of
.
Note
that both Broeils and Rhee used Bottinelli et al.'s prescription to
correct for instrumental broadening which we are forced to adopt here to
ensure a valid comparison between their and our results. We calculated
the values of
![]() and
and
![]() for which the average values
for which the average values
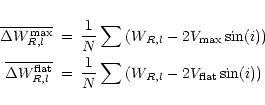
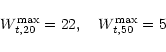
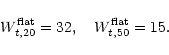
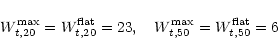
Our results are illustrated in Fig. 2 where we show, for each of the
22 galaxies, the deviations
![]() (upper panels) and
(upper panels) and
![]() (lower
panels) as a function of
(lower
panels) as a function of
![]() .
Galaxies with
.
Galaxies with
![]() are
indicated by filled symbols, galaxies with
are
indicated by filled symbols, galaxies with
![]() are indicated by open symbols. The upper two
panels in each block show the
results one obtains when using Broeil's adopted values of
Wt,20=38 and
are indicated by open symbols. The upper two
panels in each block show the
results one obtains when using Broeil's adopted values of
Wt,20=38 and
![]() .
.
From the upper panels in the upper block it is clear that the maximum
rotational velocity as derived from the corrected global profiles is
severely underestimated when using the values of Wt,l derived by
TFq and adopted by Broeils. This systematic underestimation disappears
when Wt,20 is decreased from 38 to 22 km s-1 and Wt,50 is
decreased from 14 to 5 km s-1. The upper two panels in the lower block
show that if one is interested in the amplitude of the flat part, which
is smaller than the maximum rotational velocity for galaxies with a
declining rotation curve (open symbols), the average offset becomes less
significant simply because the open symbols scatter upward. In this
case, to obtain an average zero offset, we find similar values for
Wt,l as those adopted by Broeils. However, we find the curious
situation that the corrected width of the global profile systematically
overestimates
![]() for galaxies with a
declining rotation curve (open symbols) and systematically
underestimates
for galaxies with a
declining rotation curve (open symbols) and systematically
underestimates
![]() for galaxies with a purely
flat rotation curve (filled symbols).
for galaxies with a purely
flat rotation curve (filled symbols).
From this we can conclude that, in a statistical sense, the maximum
rotational velocity of a galaxy can be reasonably well retrieved from
the width of the global profile when using
Wt,20=22 or
![]() .
The amplitude of the flat part can not be retrieved
consistently for a mixed sample containing galaxies with declining
rotation curves. Note that we have explored only a restricted range of
rotational velocities:
.
The amplitude of the flat part can not be retrieved
consistently for a mixed sample containing galaxies with declining
rotation curves. Note that we have explored only a restricted range of
rotational velocities:
![]() .
.
Our results also indicate a non-Gaussian distribution of random
velocities in the sense that
![]() .
Interpreting Wt,20 and Wt,50 in terms of velocity dispersions
it follows that
.
Interpreting Wt,20 and Wt,50 in terms of velocity dispersions
it follows that
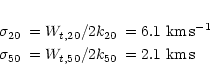
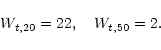
Copyright ESO 2001