8 Discussion

Figure 21: Correlation of the EW of the low velocity absorption in K I 7698Å (filled dots) and of the EW of the central absorption in H$\beta$with B-V

Figure 22: The uppermost two spectra of RW Aur A are the average spectrum and the spectrum with enhanced accretion (dashed). Below them, their difference (the differential spectrum) is shown with radial velocities indicated. At the bottom we show the spectrum of $\gamma$ Cep (K1III-IV) with line identifications and excitation potentials

The extremely complex, yet regular patterns of spectral variability, together with the "wild'' photometric behaviour of RW Aur A, challenge any attempt to model the star and its surrounding. The main result is the periodic, anti-phase variations in the radial velocities of the WALs and NELs. Such a periodicity in principle can be induced either by orbital motion of an invisible, low-mass secondary (see Paper I), which also influences the gasflows around the star, or by rotational modulation of a single star with an inclined or asymmetric magnetosphere. In the following, we present two sketches of models, which we hope can form a basis for further developments, and also provide indications of future observational tests.

Both models are critically dependent on the inclination of the stellar rotation axis and a possible stellar magnetosphere. In Paper I we discussed how the radial velocity measurements of the jets at RW Aur A can be used to restrict the range of possible orientations. Recently, C. Dougados (private communication) has communicated to us a preliminary estimate of the inclination of the counter-jet of the star, based on the proper motion and radial velocity of one knot in the jet. The inferred inclination (to the line-of-sight) is 67$\pm$4 degrees (see also Dougados et al. 2000). We adopt this value as the direction of the jet. (The gas could move faster than the knots, in which case the value is a lower limit). In addition we will assume that the jet axis is perpendicular to a circumstellar dusty disk surrounding RW Aur A, and parallel to the axis of stellar rotation.

We need to explain the following observed properties:

1.

Periodic, sinusoidal variations of the radial velocities of the WALs and NELs, and, in addition, of the equivalent widths of the NELs and the accretion components, all with a period of $P=2\hbox{$.\!\!^{\rm d}$ }77$;

2.

Anti-phase between the WAL and NEL radial velocities;

3.

The total amplitudes of the He I and He II NEL radial velocities are equal, but the average velocities are redshifted with respect to the average WAL velocity - He II significantly more than He I;

4.

A $\sim$1/4 phase-shift between the variations of the equivalent widths and radial velocities of the He I NELs;

5.

Correlation between the NEL and the accretion component equivalent widths, with a burst of accretion occurring during each cycle;

6.

Periodic variations of the equivalent widths of the BELs with about the double period, $\approx 5\hbox{$.\!\!^{\rm d}$ }5$;

7.

Anti-correlation between the BEL and accretion component equivalent widths.

Common for both models is that the observed variabilities of the red-shifted absorptions are related to the stream(s) of gas channeled by a magnetic field to hot spot(s) on the stellar surface. Stellar activity alone cannot account for all the details: non-axisymmetric accretion is present.

The broad emission lines with the blue-shifted maximum and red-shifted absorptions are most probably formed in a global magnetosphere threaded by streams of gas flowing towards the star (Calvet 1998 and references therein; Muzerolle et al. 1998). The free-fall time is much less than the period of rotation, i.e. local fluctuations in the accretion flows would result in irregular variations of the blue and red wings in the broad emission line profiles.

In projection onto the star, along the same line of sight, we see the low velocity, low temperature gas at the beginning of the accretion column, and the high velocity, high temperature gas approaching the star at the end of the accretion column (Fig. 20). The narrow emission lines of He can be formed within the same accretion column but very near the stellar surface, where the gas is already decelerated but still has some positive velocity. This explains the shifts in the mean radial velocity of NELs, and the correlation between the EWs of the NELs and the accretion components (Fig. 18). These narrow He I emission lines can be used for the detection of the magnetic field of this star, as was made for BP Tau by Johns-Krull et al. (1999).

The lines of Ba II discussed in Sect. 4 and the enhancements of the low excitation lines of Li I, K I, Ca I originate probably in the outer part of the magnetosphere, which acts like a shell. The strengths of these absorptions correlate with B-V, which may be due to the presence of dust in dense blobs of gas rising from the accretion disk. The blue-shifted "dips'' in these lines indicate that a wind component is also present in the profile. Presumably, the ultraviolet blue-shifted absorption components reported by Gahm (1970) and Errico et al. (2000) originate in the same wind outside the main accretion flows.

Finally, the light variability most certainly is due to variations both in circumstellar extinction and the continuous veiling.

The properties described above are common for both models, but the origin of the periodical modulation is different.

8.1 Binary star?

Figure 23: In our search for mechanisms explaining how the secondary may act as a generator of enhanced accretion from an area at the disk edge to a spot on the primary we discuss gravitational perturbations leading to accretion along spirals to the secondary, where some matter is deflected and continues to fall down to a spot, possibly along a trajectory tilted relative to the primary surface (upper panel). Another concept is described in the lower two panels, showing the combined magnetic field structure of two magnetic stars. The field at the secondary looks very different if the magnetic bodies have parallel (middle panel) or anti-parallel fields (lower panel). Enhanced MHD action occurs at the disk edge closest to the secondary

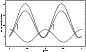Figure 24: Calculated radial velocity changes of the WALs (fulldrawn), the HeI NELs (dashed), and the HeII NEL (short-dashed). The phase whith expected maximum in the EWs of He are marked with arrows

Paper I addressed several aspects of the binary hypothesis, where it is assumed that the WAL velocity variations are due to orbital motion. First of all it is reassuring that our new observations confirm the period, amplitude and phase of the radial velocity variations of the WALs. In addition, we now have the inclination of the system (assuming that the orbital axis is aligned with the jet). We expect that the K-type primary has a mass slightly larger than 1$M_{\odot}$(see Sect. 5). It follows that the secondary is a brown dwarf (BD) of $0.04{-}0.05\,M_{\odot}$ in an orbit of low eccentricity at about 8-10$R_{\odot}$ from the primary (see Paper I). The orbital period of the secondary is $2\hbox{$.\!\!^{\rm d}$ }77$, and the centre of gravity is well inside the primary.

The basic concept of the binary star model is that the periodic spectral variability is related to the influence of a close secondary component, just like for other close binary TTSs. The He I and He II NELs cannot originate at hot spots on the secondary unless the inclination of the system is very small (Paper I). Moreover, this hot region cannot be located between the components, for instance as the result of two colliding winds, because then the amplitudes of the NEL radial velocities would be much larger than observed. However, many TTSs show narrow He I emission components thought to arise at the footpoints of global accreting flows from the disk, and we have followed this general concept.

Consequently, our discussion focusses on the following idea: global magnetospheric accretion, typical for TTSs, is present. The BELs are formed in this flow. In addition, the secondary produces enhanced accretion in one direction. This gas falls freely into regions close to the stellar surface of the primary, where deceleration and heating occurs. We have considered two possible mechanisms, which may lead to such an asymmetry of the accretion. Both these possibilities are shown schematically in Fig. 23, where the disk edge is placed at the 2:1 period resonance (i.e., the orbital period of the inner part of the disk is about $5\hbox{$.\!\!^{\rm d}$ }5$).

One possibility is that the secondary, which has cleaned a gap in the disk, also perturbs the disk. Gas spirals from the disk, preferentially to the secondary, where some matter is deflected and falls onto the primary, possibly along spiral trajectories. Similar cases have been calculated by e.g. Artymowicz & Lubow (1996), and could explain the periodic bursts of emission observed in TTSs with close massive components in elliptic orbits, like DQ Tau (Basri et al. 1997). However, we envision a secondary in a nearly circular orbit, and it is not massive. This particular case must be followed numerically, assuming an upper limit of the ellipticity of 0.2 (according to Paper I), before any conclusions about plausibility can be made.

Another possibility is that both stars are magnetic, and that the magnetospheres interact in such a way that enhanced accretion from the disk occurs along dipole magnetic field lines to the primary in the direction to the secondary. In this case, the secondary receives rather little of the accretion flow, and acts only as a generator of enhanced MHD action in a small region of the disk edge. Carlqvist (private communication) has provided the principles for a combined magnetic field from two magnetic stars (dipoles) based on early magnetospheric models. For the configurations in Fig. 23, the surface magnetic field strength of the contracting BD (radius $\sim$ $0.3\,R_{\odot}$) was assumed to be about 1/10 of that of the primary. These two cases represent parallel and anti-parallel field orientations. Note, that for enhanced MHD action to be efficient, the disk radius must be smaller or the BD magnetic field stronger than assumed in Carlqvist's calculation. The recent discovery of a large flare on a brown dwarf by Rutledge et al. (2000) shows that the magnetic field can be strong.

We have considered several possible models for how gas is channeled into a cylinder over an area ("spot'') on the primary. The narrow He I and He II lines are formed as a result of heating from an impact shock. When the secondary is closest to us, also the spot is facing us, since maximum lineflux occurs at a phase around 0.25. The spot must also be seen all the time, and is therefore located at high latitude. A similar spot may exist on the "southern'' stellar hemisphere, but is tilted out-of-view. In addition, the He lines have maximum positive velocities at phase 0.5, implying that the final impact must occur along trajectories trailing the secondary.

Figure 24 shows one example of calculations using a simple geometrical model. In this model, the centre of the primary, the spot, and the secondary are orbiting the centre of gravity. The spot co-rotates at high latitude, where the orbital motion of the spot is small. The infall is nearly radial to the normal of the surface, but strongly tilted in longitude. In this way the anti-phase variations of the WALs and NELs can be reproduced, as well as the amplitudes of the NELs. Assuming that the EWs of He are largest at maximum projected spot area, the corresponding observed $\sim$1/4 phase-shift can also be reproduced. The NELs of He I and He II are assumed to form along the same trajectory but with different average infall velocities (tracing different volumes in the cylinder). The shift in average velocity in Fig. 24 corresponds to infall velocities of 30kms^-1 (He I) and 40kms^-1 (He II).

In the binary case, part of the veiling comes from a ring around the visible pole connected to global accretion as manifested in the BELs, just as assumed for other TTSs. Superimposed is the veiling produced in the "spot''. It could be that this spot is a region of enhanced accretion in the high latitude ring. Both these components can be expected to vary irregularly and independently due to variable mass inflow. Part of the veiling may also be due to narrow emission lines, as is discussed in the subsequent section.

Referring to the model descriptions above it seems worth exploring accretion paths in the combined magnetospheres of the stars. Since the disk edge is located far outside the co-rotation radius, the global field is dragged behind, in a way similar to the solar magnetic field. The field lines can therefore be expected to be curved also in longitude. The magnetosphere of the secondary acts as the motor of channelled accretion in this case.

In conclusion, it seems that the binary hypothesis can account for most of the points set above. Many of the details are presently not very well understood, and require a much deeper analysis of the physics involved. A major item is point 6, namely the $5\hbox{$.\!\!^{\rm d}$ }5$period, which calls for an additional modulation of the BELs.

8.2 Single star?

Periodic variations in the accretion features are not unique to RW Aur A, and were observed also in other TTSs, like SU Aur (Giampapa et al. 1993; Petrov et al. 1996). As an explanation it was proposed that the periodicity is related to the axial rotation of the star. If the magnetic axis is not aligned with the rotational axis, the accreting gas gives rise not to hot rings, but to two elongated hot spots near the two magnetic poles of the star (Königl 1991). Then, the stellar rotation would modulate the brightness and the spectral features associated with the accretion. The same effect of the rotational modulation may appear if the structure of the stellar magnetic field is not perfectly symmetric, with larger magnetic loops at certain longitudes. In both cases, we have non-axisymmetric magnetospheric accretion. Note that permanent active longitudes have been found in other types of active stars (Jetsu et al. 1993; Berdyugina & Tuominen 1998).

The basic concept of the single star model of RW Aur is that the longer period of 5-6 days is the rotational period of the star, while the shorter one, about $2\hbox{$.\!\!^{\rm d}$ }77$, indicates that there are two active regions on the stellar surface - two footpoints of the accretion columns on opposite sides of the star.

The following arguments support this concept. With $R_*\geq 1.3~R_{\odot}$(Sect. 5) and $v\,\sin i=16$kms^-1the period must be $\geq 4\hbox{$.\!\!^{\rm d}$ }1$. That is, the observed 5-6 days period is more likely to be the true rotational period than the $2\hbox{$.\!\!^{\rm d}$ }77$ period. A similar period of $5\hbox{$.\!\!^{\rm d}$ }4$ was first found in variations of the H$\beta$ profile in RW Aur A in observations of 1980-82 (Grinin et al. 1983). Variations in the broad emission lines formed in a large volume of the magnetosphere and the stellar wind reflect the rotational period, while the spectral features associated with the accretion processes closer to the star reflect the local structure of the accretion channels and may show period(s) shorter than the rotational one.

Figure 25: A model of a star with two spots of chromospheric emission (solid dots), associated with the two footpoints of the accretion columns. The photospheric absorption spectrum contributes in each dot over the entire surface, while narrow emission lines only arise in the spot area

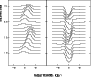Figure 26: Variations of emission and absorption line profiles in the spectrum of the spotted star (shown in Fig. 25), integrated over the stellar surface. Each spectrum corresponds to a certain phase of the axial rotation; step in phase = 1/16

The phase-shift in the variations of the radial velocities and the EW of the He I narrow emission, about 0.25, is a clear indication that the emission is formed in a spot-like area. The EW is larger when the spot is face-on to the observer, while the radial velocity is larger when the spot is near the limb. With two spots on opposite sides, this happens twice over one rotational period of about $5\hbox{$.\!\!^{\rm d}$ }5$, hence the period of $2\hbox{$.\!\!^{\rm d}$ }77$appears in the data.

The unexpected result of our research is the absence of any correlation between veiling and brightness, although both parameters were changing over wide ranges. The considerable increase of veiling at constant brightness of the star (Fig. 12) excludes the possibility that the veiling was caused by a rise in the additional continuum radiated by a hot spot (unless the increased brightness was precisely balanced by increased circumstellar extinction).

Besides the hot continuum, the veiling can be raised by narrow emission lines of neutral metals which partially fill in the photospheric absorptions. Variability in the strength of these hypothetical narrow emissions could cause variability of the veiling even at constant brightness of the star. An argument in favour of such an interpretation can be found in the spectrum taken at the highest value of the veiling (HJD 2450382.5). As was written in Sect. 3, narrow absorption components are usually present on top of many broad emission lines of neutral metals. In the spectrum taken at highest veiling, these narrow absorptions turned into narrow emissions (Fig. 9). The radial velocities of these narrow emissions of the metals correspond to that of the He I narrow emission. We may suggest that the narrow emissions of the metals form in a chromosphere-like region associated with the footpoint of the accretion column. Since we know already that the radial velocity of the He I narrow emission varies periodically, we may expect that the narrow emissions of the metals also vary in radial velocity, and this must be reflected in the variability of the photospheric line profiles distorted by these narrow emissions.

In order to check this hypothesis numerically, we calculated a synthetic spectrum from a single rotating star with two spots of "chromospheric'' emission. Figure 25 shows the positions of the two spots as they are projected onto the stellar disk at different phases during the rotation of the star. Figure 26 shows an example of line profile variations in an absorption line partially filled in with the chromospheric emission, and in a pure emission line (like He I). As the star rotates, the radial velocities of the absorption line vary in anti-phase with respect to those of the emission line, and the EWs of the emission vary with a phase-shift to the radial velocity, similar to that observed in RW Aur. The observed amplitudes and phase shifts can be reproduced with two spots of about 20 degrees in radius, located at latitudes of $\pm45^{\circ}$ at opposite longitudes, as is shown in Fig. 25. With an inclined magnetic axis the spots may be close to the magnetic poles. One may notice, however, that the velocity variations in such a model are not quite sinusoidal. Spectra with higher signal-to-noise ratios are needed to check whether the predicted absorption line distortions shown in Fig. 26 are really present. Although the hypothesis of the chromospheric emissions filling in the photospheric lines accounts for most of the observed variations, it is not clear why these emissions were never seen above the continuum level in all the photospheric lines.

The hot spots in CTTSs are not as long-living as the cool spots related to the local magnetic fields, i.e. accretion processes are not stable. Contrary to the case of a binary star, the variations in the radial velocities caused by the spot effect described above may disappear sometimes. This could be an observational test to distinguish between the two models.