

Up: Hamiltonian formulation of the
Subsections
Table 1:
Uranian satellite system: co-orbital frequencies
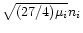 and forcing frequencies gi-gj and fi-fj (units are rads/day).
Note that gi-gj and fj-fi are nearly equal; this is due to
the fact that gk and fkare respectively the eigenvalues of matrices A and B which by definition
have
Akk=-Bkk and which are also nearly diagonal (the diagonal term
is mostly due to the oblateness and therefore
and forcing frequencies gi-gj and fi-fj (units are rads/day).
Note that gi-gj and fj-fi are nearly equal; this is due to
the fact that gk and fkare respectively the eigenvalues of matrices A and B which by definition
have
Akk=-Bkk and which are also nearly diagonal (the diagonal term
is mostly due to the oblateness and therefore
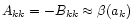 )
)
| i |
 |
g1-gi |
g2-gi |
g3-gi |
g4-gi |
g5-gi |
| |
|
f1-fi |
f2-fi |
f3-fi |
f4-fi |
f5-fi |
| 1 |
1.1 10-2 |
0 |
-7.0 10-4 |
-8.5 10-4 |
-9.1 10-4 |
-9.7 10-4 |
| |
|
0 |
7.0 10-4 |
8.5 10-4 |
9.1 10-4 |
9.7 10-4 |
| 2 |
2.9 10-2 |
7.0 10-4 |
0 |
-1.5 10-4 |
-2.1 10-4 |
-2.7 10-4 |
| |
|
-7.0 10-4 |
0 |
1.5 10-4 |
2.1 10-4 |
2.8 10-4 |
| 3 |
1.3 10-2 |
8.5 10-4 |
1.5 10-4 |
0 |
-6.0 10-5 |
-1.2 10-4 |
| |
|
-8.5 10-4 |
-1.5 10-4 |
0 |
5.4 10-5 |
1.2 10-4 |
| 4 |
1.1 10-2 |
9.1 10-4 |
2.1 10-4 |
6.0 10-5 |
0 |
-6.1 10-5 |
| |
|
-9.0 10-4 |
-2.1 10-4 |
-5.4 10-5 |
0 |
6.9 10-5 |
| 5 |
7.0 10-3 |
9.7 10-4 |
2.7 10-4 |
1.2 10-4 |
6.1 10-5 |
0 |
| |
|
-9.7 10-4 |
-2.8 10-4 |
-1.2 10-4 |
-6.9 10-5 |
0 |
We will now apply our secular theory to the case of Trojan orbits
associated with the five major uranian satellites.
As already noticed in Paper I,
this system provides a good testing ground for our theory due to two reasons.
First: there are no mean motion resonances amongst these satellites and thus
the secular approximation (i.e. the average of the disturbing
potential over the mean longitudes) is valid.
Second: these satellites have nearly-circular and nearly-equatorial orbits
thus satisfying the requirements of our secular theory.
We used the data from Malhotra et al. (1989) to
calculate the parameters of the secular theory for the uranian
system![[*]](/icons/foot_motif.gif) and then identified the modes that satisfy
Eq. (87) (or Eq. (88)) inside the co-orbital
regions of its major satellites.
For instance, in order to locate secular resonances involving
the pericentres (or nodes) inside the co-orbital region of the mass mk, we
first plot
and then identified the modes that satisfy
Eq. (87) (or Eq. (88)) inside the co-orbital
regions of its major satellites.
For instance, in order to locate secular resonances involving
the pericentres (or nodes) inside the co-orbital region of the mass mk, we
first plot 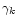 (or
(or 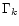 )
)![[*]](/icons/foot_motif.gif) as a function of a0 (a parameter that
characterizes the size of the tadpole or horseshoe orbit already defined in
Eq. (14)) and then identify the intersection with the
horizontal lines taken at
as a function of a0 (a parameter that
characterizes the size of the tadpole or horseshoe orbit already defined in
Eq. (14)) and then identify the intersection with the
horizontal lines taken at
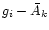 (or
(or
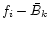 ).
We show the location of the secular resonances
which occur inside the co-orbital regions of Miranda (m1), Ariel (m2),
Umbriel (m3), Titania (m4) and Oberon (m5) in Fig. 2.
Note that we can condense the results for the five satellites in
one single picture due to the fact that both
).
We show the location of the secular resonances
which occur inside the co-orbital regions of Miranda (m1), Ariel (m2),
Umbriel (m3), Titania (m4) and Oberon (m5) in Fig. 2.
Note that we can condense the results for the five satellites in
one single picture due to the fact that both 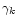 and
and 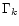 scale as
scale as 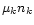 (see also Paper I).
(see also Paper I).
We also used a Runge-Kutta-Nystron 12th order scheme (Brankin et al. 1987) to
integrate the equations of motion of the system consisting of
Uranus, its satellites and associated test particles in tadpole or horseshoe orbits.
The parameters and initial conditions were again taken from Malhotra et al.
(1989), and we incorporated an oblateness potential
which takes into account only the dominant zonal harmonic.
In Paper I we showed the result of a numerical integration
for a test particle located near the L4 point of Titania (m4), which
included the gravitational interaction with Umbriel (m3) only.
We saw that in this
case the long-term behaviour of
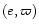 is affected by the
proximity of a secular resonance involving the mode g3 and is in
good agreement with the secular solution (Eq. (97)). In fact,
we can see from Table 1 that the adiabatic approximation made in Sect. 3.3.2
should be valid in the case of the uranian satellites, as the
co-orbital frequencies are much larger than the forcing frequencies.
is affected by the
proximity of a secular resonance involving the mode g3 and is in
good agreement with the secular solution (Eq. (97)). In fact,
we can see from Table 1 that the adiabatic approximation made in Sect. 3.3.2
should be valid in the case of the uranian satellites, as the
co-orbital frequencies are much larger than the forcing frequencies.
 |
Figure 2:
Location of secular resonances involving
a) the pericentres and b) the nodes, inside the co-orbital regions of
the uranian satellites Miranda (m1), Ariel (m2), Umbriel (m3),
Titania (m4) and Oberon (m5).
Secular resonances associated with the modes gi (or fi) occur
at the locations
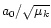 determined by the intersections of
the curves
determined by the intersections of
the curves 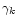 (or
(or 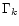 )
with
the lines labeled Ak-gi (or Bk-fi).
Note that the frequencies )
with
the lines labeled Ak-gi (or Bk-fi).
Note that the frequencies 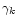 and
and 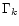 were divided
by
were divided
by 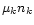 in order to be able to condense the results for all the
five satellites in one single picture.
The singularity in
in order to be able to condense the results for all the
five satellites in one single picture.
The singularity in 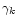 and
and 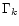 at
at
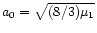 corresponds to the tadpole-horseshoe separatrix corresponds to the tadpole-horseshoe separatrix |
In Fig. 3 we show the evolution of an orbit
located near the L4 point of Oberon with a0=0. This is very close
to the secular resonance involving the mode g4 (cf. Fig. 2)
and we see that the slow periodic motion of the critical argument
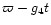 is correlated with a large amplitude oscillation of the
eccentricity.
The small amplitude fast oscillation in the eccentricity has the same
periodicity as the argument
is correlated with a large amplitude oscillation of the
eccentricity.
The small amplitude fast oscillation in the eccentricity has the same
periodicity as the argument
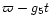 and is indeed
caused by the forced term due to the 1:1 mean motion resonance with
Oberon.
There is no apparent threat to the long-term stability of this orbit, as
the maximum eccentricity is still very far
from the threshold required for close approaches with nearby Titania
(i.e. e=0.25).
and is indeed
caused by the forced term due to the 1:1 mean motion resonance with
Oberon.
There is no apparent threat to the long-term stability of this orbit, as
the maximum eccentricity is still very far
from the threshold required for close approaches with nearby Titania
(i.e. e=0.25).
In Fig. 4 we show the evolution of a
horseshoe orbit associated with Oberon which has
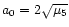 .
The eccentricity exhibits very irregular behaviour which is probably due to
the interaction between two nearby secular resonances (involving the modes
g3 and g4; cf. Fig. 2) as suggested by the
behaviour of the associated critical arguments. Due to the overlap
of the separatrices of these two secular resonances, the eccentricity diffuses
chaotically and can potentially reach stability-threatening values.
.
The eccentricity exhibits very irregular behaviour which is probably due to
the interaction between two nearby secular resonances (involving the modes
g3 and g4; cf. Fig. 2) as suggested by the
behaviour of the associated critical arguments. Due to the overlap
of the separatrices of these two secular resonances, the eccentricity diffuses
chaotically and can potentially reach stability-threatening values.
 |
Figure 3:
Evolution of eccentricity (upper figure), critical arguments
associated with the modes g4 (middle figure) and g5 (lower figure)
for an orbit located near Oberon's L4 point with a0=0.
Time is in units of Miranda's orbital period |
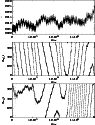 |
Figure 4:
Evolution of eccentricity (upper figure), critical arguments
associated with the modes g3 (middle figure) and g4 (lower figure)
for a horseshoe orbit associated with Oberon with
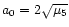 .
Time is in units of Miranda's orbital period .
Time is in units of Miranda's orbital period |
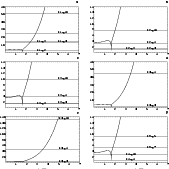 |
Figure 5:
Location of secular resonances involving the
pericentres inside the co-orbital regions of the planets.
The frequencies shown in the vertical axes are adimensional
and correspond to the true frequencies divided by 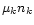 .
Secular resonances associated with the modes gi occur
at the locations .
Secular resonances associated with the modes gi occur
at the locations
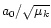 determined by the intersections
of the lines labeled Ak-gi with the curves
determined by the intersections
of the lines labeled Ak-gi with the curves 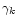 .
The secular resonances involving the modes g1 and g2 (not shown
here as they are likely to be very weak) also occur
inside the co-orbital regions of Uranus and Neptune .
The secular resonances involving the modes g1 and g2 (not shown
here as they are likely to be very weak) also occur
inside the co-orbital regions of Uranus and Neptune |
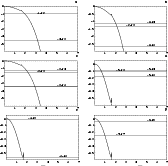 |
Figure 6:
Location of secular resonances involving the nodes
inside the co-orbital regions of the planets.
The frequencies shown in the vertical axes are adimensional
and correspond to the true frequencies divided by 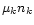 .
Secular resonances associated with the modes fi occur
at the locations .
Secular resonances associated with the modes fi occur
at the locations
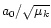 determined by the intersections
of the lines labeled Bk-fi with the curves
determined by the intersections
of the lines labeled Bk-fi with the curves 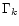 |
We remark here that although our secular theory cannot describe
accurately the true behaviour in the very close vicinity of secular resonances
(due to the occurrence of singularities in Eqs. (97) and
(99) which is an artifact caused by the truncation of the
disturbing potential at degree two in e and I) or whenever there is
overlap of adjacent secular resonances (due to the underlying chaotic nature
of the phase space), it is still very useful in the sense that it allows us
to obtain the location of these secular resonances, whose dynamical effect
can always be subsequently investigated with numerical integrations.
We also applied our secular theory to the system consisting of the eight
planets, Mercury to Neptune, using values for the eigen-frequencies of the
secular system from Brouwer & Van Woerkom (1950). As these
were calculated taking in account the effect of the 2:5 near
commensurability
between the orbital periods of Jupiter and Saturn, the secular
system is characterised by ten eigen-frequencies gi (with
g9=2 g5-g6 and
g10=2 g6-g5) and eight eigen-frequencies fi.
We then used these in order to obtain the locations of secular
resonances inside
the planetary co-orbital regions![[*]](/icons/foot_motif.gif) condensed in the six panels of Figs. 5 and 6.
condensed in the six panels of Figs. 5 and 6.
Figure 5f proves that the secular resonances involving the modes
g6 and g10 can affect Saturn's tadpole orbits which
is in agreement with recent numerical integrations by Marzari & Scholl
(2000).
In particular, these latter authors suggest that the mixed secular resonance
involving the mode g10 is the major factor responsible for the
destabilization of tadpole orbits associated with Saturn.
In Fig. 6b we see that the secular resonances involving the modes f3 and f4occur very close to each other inside Venus' horseshoe region, thus suggesting
their possible overlap. In fact, the numerical integrations of Michel
(1997)
showed that a clone of asteroid (4660) Nereus becomes, at some stage in its
life, a Venus' horseshoe orbit which exhibits chaotic diffusion of the
inclination caused by the overlap of these two secular resonances.
From Fig. 6d and as already mentioned in Paper I, we see that the secular
resonance
involving the mode f6 occurs within Jupiter's tadpole region.
Recent numerical integrations by Marzari & Scholl (2000) seem to
support earlier suggestions by Yoder (1979) and Milani
(1994) concerning the important role
played by this secular resonance in the dynamical shaping of the Trojan cloud.


Up: Hamiltonian formulation of the
Copyright ESO 2001




