

Up: Hamiltonian formulation of the
Subsections
We now recall Sect. 2.1.2 where we obtained the Hamiltonian of the averaged
problem (Eq. (23)) and then
apply Eq. (13) in order to write its first-order part
(Eq. (24)) as
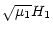 |
= |
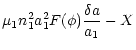 |
(42) |
where 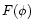 is a function of
is a function of 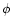 ,
,
and
![\begin{displaymath}
\begin{array}{l @{\hspace{2cm}} l}
-\varpi & M=\frac{1}{2} n a^2 e^2 \\ [2mm]
-\Omega & N=\frac{1}{2} n a^2 I^2
\end{array}\end{displaymath}](/articles/aa/full/2001/14/aa10378/img126.gif) |
(44) |
is an approximate canonical set of coordinates and conjugate momenta
for the secular Hamiltonian (i.e. the Hamiltonian obtained after the
elimination of the 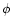 -dependence).
-dependence).
By construction of the Hamiltonian of the averaged problem (Eq. (23))
the variables
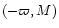 and
and
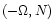 vary on a timescale
vary on a timescale
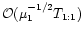 and therefore are much slower than
and therefore are much slower than
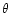 ,
the angle variable of the integrable part H0.
The general procedure for dealing with this type of quasi-integrable systems
involves a canonical transformation of variables such that the new
Hamiltonian does not depend on the fast angle
and thus the associated action is an adiabatic invariant
(Lichtenberg & Lieberman 1983).
To first-order in the small parameter
,
the angle variable of the integrable part H0.
The general procedure for dealing with this type of quasi-integrable systems
involves a canonical transformation of variables such that the new
Hamiltonian does not depend on the fast angle
and thus the associated action is an adiabatic invariant
(Lichtenberg & Lieberman 1983).
To first-order in the small parameter
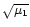 ,
the transformed
Hamiltonian is
,
the transformed
Hamiltonian is
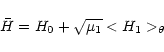 |
(45) |
where
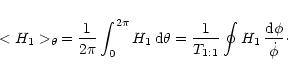 |
(46) |
Now from Eq. (8)
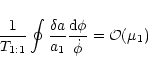 |
(47) |
hence we obtain the transformed Hamiltonian
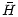 |
= |
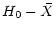 |
(48) |
with
where (k,h) and (q,p) are defined as
 |
(50) |
Moreover,
![\begin{displaymath}g_i[l]=\frac{1}{T_{1:1}} \oint g_i(\phi) \frac{{\rm d}\, \phi}{\dot{\phi}}
\end{displaymath}](/articles/aa/full/2001/14/aa10378/img143.gif) |
(51) |
where l is a parameter that characterises the size of the tadpole or
horseshoe orbit which we define as
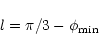 |
(52) |
and
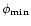 is the minimal distance to m1 obtained
by solving Eq. (12) with
is the minimal distance to m1 obtained
by solving Eq. (12) with
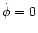 .
.
From Paper I we recall that
![$\bar{g}_5[l]=-2 \bar{g}_4[l]$](/articles/aa/full/2001/14/aa10378/img147.gif) and
and
![$\bar{g}_6[l]=0$](/articles/aa/full/2001/14/aa10378/img148.gif) ;
then we write
;
then we write![[*]](/icons/foot_motif.gif)
![$\displaystyle 2 \bar{g}_4[l] \mu_1 n_1$](/articles/aa/full/2001/14/aa10378/img150.gif) |
= |
![$\displaystyle \Gamma[l]$](/articles/aa/full/2001/14/aa10378/img151.gif) |
(53) |
![$\displaystyle 2 \bar{g}_1[l] \mu_1 n_1$](/articles/aa/full/2001/14/aa10378/img152.gif) |
= |
![$\displaystyle \gamma[l]$](/articles/aa/full/2001/14/aa10378/img153.gif) |
(54) |
![$\displaystyle \frac{\bar{g}_2[l]}{2 \bar{g}_1[l]}$](/articles/aa/full/2001/14/aa10378/img154.gif) |
= |
![$\displaystyle - c[l] \cos{b[l]}$](/articles/aa/full/2001/14/aa10378/img155.gif) |
(55) |
![$\displaystyle \frac{\bar{g}_3[l]}{2 \bar{g}_1[l]}$](/articles/aa/full/2001/14/aa10378/img156.gif) |
= |
![$\displaystyle - c[l] \sin{b[l]}.$](/articles/aa/full/2001/14/aa10378/img157.gif) |
(56) |
We also note that from Eq. (14) we have
![\begin{displaymath}a_0[l]=\sqrt{\frac{8}{3} \mu_1 \left( f(\pi/3-l)-\frac{3}{2} \right)}
\end{displaymath}](/articles/aa/full/2001/14/aa10378/img158.gif) |
(57) |
and we refer to Paper I for plots of
![$\Gamma[l]$](/articles/aa/full/2001/14/aa10378/img159.gif) ,
,
![$\gamma[l]$](/articles/aa/full/2001/14/aa10378/img160.gif) ,
c[l] and b[l] as functions of
a0[l].
,
c[l] and b[l] as functions of
a0[l].
We now write Hamilton's equations for (k,h) as
which imply the solution for
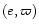
i.e. composed of a proper term
(proper eccentricity 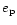 and proper precession frequency
and proper precession frequency ![$\gamma[l]$](/articles/aa/full/2001/14/aa10378/img160.gif) )
and a forced term (forced eccentricity c[l] e1 and forced periapse b[l]).
)
and a forced term (forced eccentricity c[l] e1 and forced periapse b[l]).
Similarly, we write Hamilton's equations for (q,p) as
which imply the solution for
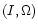
![\begin{displaymath}
I \exp[{\rm i} \Omega]=I_{\rm p} \exp[{\rm i}(\Gamma[l] t+\Xi)]+
I_1 \exp[{\rm i} \Omega_1]
\end{displaymath}](/articles/aa/full/2001/14/aa10378/img173.gif) |
(61) |
i.e. composed of a proper term
(proper inclination 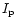 and proper precession frequency
and proper precession frequency ![$\Gamma[l]$](/articles/aa/full/2001/14/aa10378/img159.gif) )
and a forced term I1 (note, however, that if we choose the orbital plane of
)
and a forced term I1 (note, however, that if we choose the orbital plane of
 and m1 as reference, then this forced term disappears).
and m1 as reference, then this forced term disappears).
The Hamiltonian of the averaged problem has now six degrees of freedom
(cf. Sect. 2.2) i.e. two more than in the restricted three-body case.
However, we can eliminate these extra degrees of freedom
by making a canonical transformation to the following variables
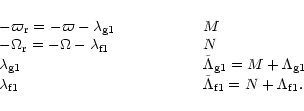 |
(62) |
The transformed first-order part of the Hamiltonian (Eq. (32)) is
then
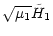 |
= |
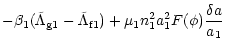 |
|
| |
|
- X - Y |
(63) |
with
and
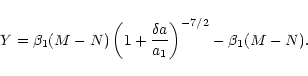 |
(65) |
The first term on the right hand side of Eq. (63)
can be dropped as there is no explicit dependence on
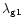 or
or
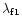 .
Hence, Eq. (63) has the same form as Eq. (42),
except for the term Y.
This introduces the relative precession frequencies
.
Hence, Eq. (63) has the same form as Eq. (42),
except for the term Y.
This introduces the relative precession frequencies
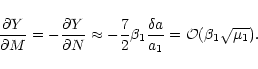 |
(66) |
As in general
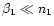 ,
the variables
,
the variables
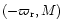 and
and
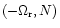 still vary on a time-scale much longer than the co-orbital period
still vary on a time-scale much longer than the co-orbital period
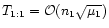 .
We can then follow the procedure described previously, obtaining
an Hamiltonian as defined by Eqs. (45) and (46),
i.e.
.
We can then follow the procedure described previously, obtaining
an Hamiltonian as defined by Eqs. (45) and (46),
i.e.
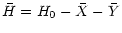 |
|
|
(67) |
with
and
![\begin{displaymath}\bar{Y}= \frac{1}{2} \Delta\bar{\beta}
[(h_{\rm r}^2+k_{\rm r}^2)-(p_{\rm r}^2+q_{\rm r}^2)]
\end{displaymath}](/articles/aa/full/2001/14/aa10378/img194.gif) |
(69) |
where
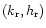 and
and
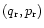 are
defined as
are
defined as
 |
(70) |
and from Eq. (30)
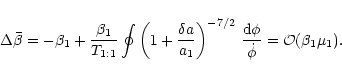 |
(71) |
Hamilton's equations for
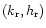 are
are
![$\displaystyle \dot{k}_{\rm r}+{\rm i} \dot{h}_{\rm r} =
\left(-{\partial \over ...
...\rm i} h_{\rm r})
-{\rm i} \gamma[l] \sqrt{n_1} a_1 c[l] e_1 \exp[{\rm i} b[l]]$](/articles/aa/full/2001/14/aa10378/img199.gif) |
|
|
(72) |
and therefore the solution for
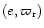 is
is
![$\displaystyle e \exp[{\rm i} \varpi_{\rm r}] = e_{\rm p} \exp[{\rm i}((\gamma[l...
...i)] +\frac{\gamma[l] c[l] e_1 \exp[{\rm i} b[l]]}{\gamma[l]+\Delta\bar{\beta}}.$](/articles/aa/full/2001/14/aa10378/img201.gif) |
|
|
(73) |
Similarly, Hamilton's equations for
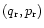 are
are
and therefore the solution for
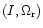 is
is
![$\displaystyle I \exp[{\rm i}\Omega_{\rm r}] = I_{\rm p} \exp[{\rm i}
((\Gamma[l...
...lta\bar{\beta}) t+\Xi)] +\frac{\Gamma[l] I_1}{\Gamma[l]-\Delta\bar{\beta}}\cdot$](/articles/aa/full/2001/14/aa10378/img206.gif) |
|
|
(75) |
From Eqs. (73) and (75)
we see that the oblateness term,
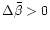 ,
leads to a decrease
in the secular precession periods and the magnitude of the forced terms.
However, this effect is only significant if
,
leads to a decrease
in the secular precession periods and the magnitude of the forced terms.
However, this effect is only significant if
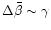 (or
(or 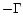 ).
As
).
As
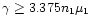 (see Fig. 1a in Paper I) and in general
(see Fig. 1a in Paper I) and in general
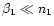 ,
one can largely neglect the term
,
one can largely neglect the term
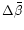 in that which concerns the evolution of the eccentricity;
in this case the secular solution reduces to Eq. (59).
On the other hand, very small amplitude
tadpole orbits can have
in that which concerns the evolution of the eccentricity;
in this case the secular solution reduces to Eq. (59).
On the other hand, very small amplitude
tadpole orbits can have
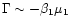 (see Fig. 1d in Paper I) and thus the effect of the term
(see Fig. 1d in Paper I) and thus the effect of the term
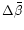 on the evolution of the inclination can be visible.
on the evolution of the inclination can be visible.
The Hamiltonian of the averaged problem has
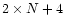 degrees of freedom
(cf. Sect. 2.3).
In order to reduce the number of degrees of freedom we perform a canonical
transformation to the following variables
degrees of freedom
(cf. Sect. 2.3).
In order to reduce the number of degrees of freedom we perform a canonical
transformation to the following variables
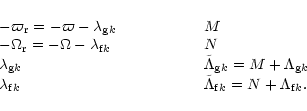 |
(76) |
We also perform N-1 canonical transformations of
the same type to the following variables
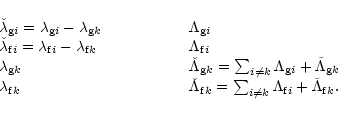 |
(77) |
Then, the transformed first-order part of the Hamiltonian (Eq. (40)) is
with
and
| Y |
= |
(Ak-gk) M +(Bk-fk) N |
|
| |
|
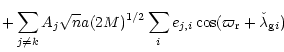 |
|
| |
|
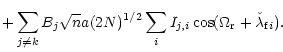 |
(80) |
And the first two terms on the right hand side of Eq. (78)
can be dropped as there
is no explicit dependence on
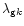 or
or
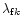 .
.
We now assume
that the perturbers move on circular and co-planar orbits, in which
case the terms in Eq. (78) depending on
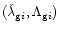 and
and
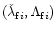 also disappear and the Hamiltonian reduces to
also disappear and the Hamiltonian reduces to
Equation (81) represents a one-degree of freedom (hence integrable)
system depending on the parameters M and N.
Therefore, we can perform a canonical transformation to action-angle
variables which eliminates 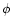 from the Hamiltonian
(Lichtenberg & Lieberman 1983).
To first-order in the small parameter
from the Hamiltonian
(Lichtenberg & Lieberman 1983).
To first-order in the small parameter
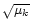 ,
this is accomplished by averaging over the angle variable of the
zero-order term H0,
which is equivalent to averaging over the co-orbital period T1:1.
The transformed Hamiltonian is
,
this is accomplished by averaging over the angle variable of the
zero-order term H0,
which is equivalent to averaging over the co-orbital period T1:1.
The transformed Hamiltonian is
![\begin{displaymath}\bar{H}=H_0-(\gamma_k[l] +\bar{A}_k-g_k) M -(\Gamma_k[l]+\bar{B}_k-f_k) N
\end{displaymath}](/articles/aa/full/2001/14/aa10378/img235.gif) |
(82) |
which has proper frequencies
where
![$\gamma_k[l]=2 \bar{g}_1[l] \mu_k n_k$](/articles/aa/full/2001/14/aa10378/img240.gif) ,
,
![$\Gamma_k[l]=2 \bar{g}_4[l] \mu_k n_k$](/articles/aa/full/2001/14/aa10378/img241.gif) ;
and from Eq. (38)
;
and from Eq. (38)
Secular resonances involving the pericentres (or nodes) occur when
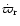 (or
(or
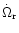 )
is equal to
a forcing frequency gi-gk (or fi-fk), i.e. when
)
is equal to
a forcing frequency gi-gk (or fi-fk), i.e. when
![$\displaystyle \gamma_k[l]+\bar{A}_k=g_i$](/articles/aa/full/2001/14/aa10378/img248.gif) |
|
|
(87) |
![$\displaystyle \Gamma_k[l]+\bar{B}_k=f_i.$](/articles/aa/full/2001/14/aa10378/img249.gif) |
|
|
(88) |
Note that the proper frequencies of precession of the Trojan orbit are
in fact
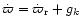 and
and
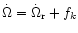 which coincide
respectively with the left hand side of Eq. (87) and Eq. (88).
Moreover, the terms
which coincide
respectively with the left hand side of Eq. (87) and Eq. (88).
Moreover, the terms 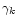 (and
(and 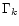 )
and the terms
)
and the terms 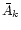 (and
(and 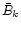 )
are respectively the contribution from the mass mk and
the contribution from the additional massive bodies mj
(where
)
are respectively the contribution from the mass mk and
the contribution from the additional massive bodies mj
(where 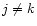 ).
).
We will now assume that not only the variables
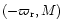 and
and
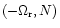 but also the angles
but also the angles
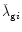 and
and
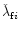 vary on a time-scale much longer than the co-orbital period T1:1.
Note that while the first assumption will in general be true, the
same does not necessarily apply to the second assumption.
When the co-orbital frequency is comparable to one of the forcing
frequencies, a low order resonance can occur in which case the adiabatic
approximation does not provide a good description of the system.
Nevertheless, if we ignore this possibility then we can
apply Eqs. (45) and (46) to obtain the
transformed Hamiltonian
vary on a time-scale much longer than the co-orbital period T1:1.
Note that while the first assumption will in general be true, the
same does not necessarily apply to the second assumption.
When the co-orbital frequency is comparable to one of the forcing
frequencies, a low order resonance can occur in which case the adiabatic
approximation does not provide a good description of the system.
Nevertheless, if we ignore this possibility then we can
apply Eqs. (45) and (46) to obtain the
transformed Hamiltonian
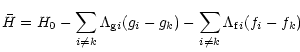 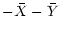 |
|
|
(89) |
with
and
where
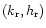 and
and
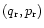 are defined as
are defined as
and from Eq. (38)
The evolution of
![$z=\sqrt{n_k} a_k e \exp[{\rm i} \varpi]$](/articles/aa/full/2001/14/aa10378/img275.gif) is described by
is described by
which is the equation of a forced harmonic oscillator with
proper frequency
![$\gamma_k[l]+\bar{A}_{k}$](/articles/aa/full/2001/14/aa10378/img279.gif) and forcing frequencies gi;
hence the solution for
and forcing frequencies gi;
hence the solution for
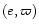 is
is
![$\displaystyle e \exp[{\rm i} \varpi]=
e_{\rm p}\exp[{\rm i}((\gamma_k[l]+\bar{A...
...}\bar{A}_{j} e_{j,i}}
{\gamma_k[l]+\bar{A}_{k}-g_i}\exp[{\rm i}(g_i t+\chi_i)].$](/articles/aa/full/2001/14/aa10378/img280.gif) |
|
|
(97) |
The evolution of
![$Z=\sqrt{n_k} a_k I \exp[{\rm i} \Omega]$](/articles/aa/full/2001/14/aa10378/img281.gif) is described by
is described by
which is the equation of a forced harmonic oscillator with
proper frequency
![$\Gamma_k[l]+\bar{B}_{k}$](/articles/aa/full/2001/14/aa10378/img285.gif) and forcing frequencies fi;
hence the solution for
and forcing frequencies fi;
hence the solution for
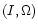 is
is
| |
|
![$\displaystyle I \exp[{\rm i} \Omega]=
I_{\rm p}\exp[{\rm i}((\Gamma_k[l]+\bar{B}_{k}) t+\Xi)]$](/articles/aa/full/2001/14/aa10378/img286.gif) |
|
| |
|
![$\displaystyle +\sum_{i} \frac{\Gamma_k[l] I_{k,i}-\sum_{j\neq k}\bar{B}_{j} I_{j,i}}
{\Gamma_k[l]+\bar{B}_{k}-f_i}\exp[{\rm i}(f_i t+\Xi_i)].$](/articles/aa/full/2001/14/aa10378/img287.gif) |
(99) |
We now recall from Paper I that
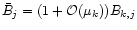 ,
and that
by definition of eigen-values and eigen-vectors,
,
and that
by definition of eigen-values and eigen-vectors,
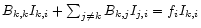 ,
so that
,
so that
This is to say that when
![$\Gamma_k[l]+\bar{B}_{k}=f_{i}$](/articles/aa/full/2001/14/aa10378/img294.gif) ,
the forcing
terms in the second-order differential equation that describes the evolution
of
,
the forcing
terms in the second-order differential equation that describes the evolution
of
![$I \exp[{\rm i} \Omega]$](/articles/aa/full/2001/14/aa10378/img295.gif) are smaller than in the
non-resonant case by a mass ratio factor. Indeed, one can show that these
forcing terms have amplitudes
are smaller than in the
non-resonant case by a mass ratio factor. Indeed, one can show that these
forcing terms have amplitudes
![$I_{k,i} (\Gamma_k[l]+\bar{B}_{k}+f_{i}) [(\Gamma_k[l]+\bar{B}_{k}-f_{i})+
{\cal O}(\mu_k \mu_i)]$](/articles/aa/full/2001/14/aa10378/img296.gif) ,
which reduce to
,
which reduce to
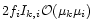 at the exact resonance.
at the exact resonance.
Note that although the secular solution obtained here
(Eqs. (97) and
(99)) has essentially the same form
as that obtained in Paper I, the terms 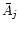 and
and 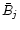 are
now defined as averages over T1:1 (which nonetheless
coincide, to lowest order, with the quantities defined in Paper I).
The basic improvement with respect to Paper I is the correct derivation of the
thresholds of validity of the secular solution which as we have seen now
simply depends on the validity of the adiabatic approximation.
are
now defined as averages over T1:1 (which nonetheless
coincide, to lowest order, with the quantities defined in Paper I).
The basic improvement with respect to Paper I is the correct derivation of the
thresholds of validity of the secular solution which as we have seen now
simply depends on the validity of the adiabatic approximation.


Up: Hamiltonian formulation of the
Copyright ESO 2001
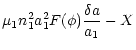
![]() and
and
![]() vary on a timescale
vary on a timescale
![]() and therefore are much slower than
and therefore are much slower than
![]() ,
the angle variable of the integrable part H0.
The general procedure for dealing with this type of quasi-integrable systems
involves a canonical transformation of variables such that the new
Hamiltonian does not depend on the fast angle
and thus the associated action is an adiabatic invariant
(Lichtenberg & Lieberman 1983).
To first-order in the small parameter
,
the angle variable of the integrable part H0.
The general procedure for dealing with this type of quasi-integrable systems
involves a canonical transformation of variables such that the new
Hamiltonian does not depend on the fast angle
and thus the associated action is an adiabatic invariant
(Lichtenberg & Lieberman 1983).
To first-order in the small parameter
![]() ,
the transformed
Hamiltonian is
,
the transformed
Hamiltonian is
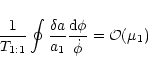

![\begin{displaymath}g_i[l]=\frac{1}{T_{1:1}} \oint g_i(\phi) \frac{{\rm d}\, \phi}{\dot{\phi}}
\end{displaymath}](/articles/aa/full/2001/14/aa10378/img143.gif)
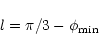
![]() and
and
![]() ;
then we write
;
then we write![]()
![\begin{displaymath}a_0[l]=\sqrt{\frac{8}{3} \mu_1 \left( f(\pi/3-l)-\frac{3}{2} \right)}
\end{displaymath}](/articles/aa/full/2001/14/aa10378/img158.gif)
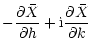
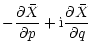
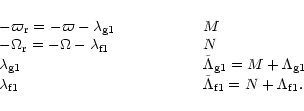
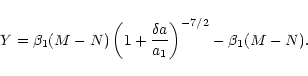
![]() or
or
![]() .
Hence, Eq. (63) has the same form as Eq. (42),
except for the term Y.
This introduces the relative precession frequencies
.
Hence, Eq. (63) has the same form as Eq. (42),
except for the term Y.
This introduces the relative precession frequencies
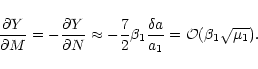
![\begin{displaymath}\bar{Y}= \frac{1}{2} \Delta\bar{\beta}
[(h_{\rm r}^2+k_{\rm r}^2)-(p_{\rm r}^2+q_{\rm r}^2)]
\end{displaymath}](/articles/aa/full/2001/14/aa10378/img194.gif)

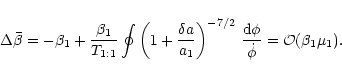
![]() are
are
![]() degrees of freedom
(cf. Sect. 2.3).
In order to reduce the number of degrees of freedom we perform a canonical
transformation to the following variables
degrees of freedom
(cf. Sect. 2.3).
In order to reduce the number of degrees of freedom we perform a canonical
transformation to the following variables
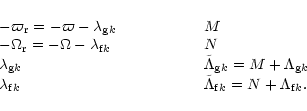
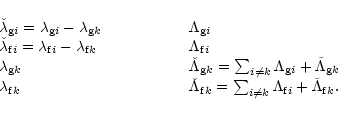
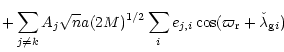
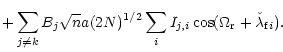
![]() and
and
![]() also disappear and the Hamiltonian reduces to
also disappear and the Hamiltonian reduces to
![\begin{displaymath}\bar{H}=H_0-(\gamma_k[l] +\bar{A}_k-g_k) M -(\Gamma_k[l]+\bar{B}_k-f_k) N
\end{displaymath}](/articles/aa/full/2001/14/aa10378/img235.gif)

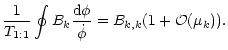
![]() and
and
![]() but also the angles
but also the angles
![]() and
and
![]() vary on a time-scale much longer than the co-orbital period T1:1.
Note that while the first assumption will in general be true, the
same does not necessarily apply to the second assumption.
When the co-orbital frequency is comparable to one of the forcing
frequencies, a low order resonance can occur in which case the adiabatic
approximation does not provide a good description of the system.
Nevertheless, if we ignore this possibility then we can
apply Eqs. (45) and (46) to obtain the
transformed Hamiltonian
vary on a time-scale much longer than the co-orbital period T1:1.
Note that while the first assumption will in general be true, the
same does not necessarily apply to the second assumption.
When the co-orbital frequency is comparable to one of the forcing
frequencies, a low order resonance can occur in which case the adiabatic
approximation does not provide a good description of the system.
Nevertheless, if we ignore this possibility then we can
apply Eqs. (45) and (46) to obtain the
transformed Hamiltonian
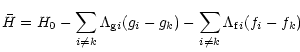
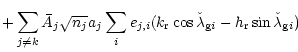
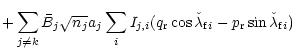
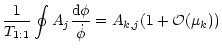
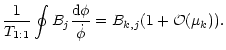
![]() is described by
is described by
![]() and
and ![]() are
now defined as averages over T1:1 (which nonetheless
coincide, to lowest order, with the quantities defined in Paper I).
The basic improvement with respect to Paper I is the correct derivation of the
thresholds of validity of the secular solution which as we have seen now
simply depends on the validity of the adiabatic approximation.
are
now defined as averages over T1:1 (which nonetheless
coincide, to lowest order, with the quantities defined in Paper I).
The basic improvement with respect to Paper I is the correct derivation of the
thresholds of validity of the secular solution which as we have seen now
simply depends on the validity of the adiabatic approximation.